Изучение самопроизвольного формирования структур в самых разнообразных явлениях позволяет выявить общие эволюционные концепции проявляющиеся в естествознании. Идеи И. Пригожина позволили доказать, что в открытых системах могут образовываться и длительное время существовать упорядоченные структуры, возникающие в результате совместного кооперативного, или, по Г. Хакену, синергетического действия. При внешнем воздействии на систему возникающие флуктуации увеличиваются и распространяются на всю систему. Новая структура всегда является результатом неустойчивости и возникает из флуктуаций.
Для получения новых материалов используются фазовые превращения в сплавах, происходящие при изменении температуры. В этом случае рассматривается открытая система, подвергающаяся притоку энергии извне. При этом формируется сильно неравновесное состояние, в котором действуют закономерности, общие для неравновесной термодинамики. Создаются предпосылки, при которых образуются новые пространственно-организованные структуры. Проблема адекватности результатов и их уточнения появляется при переходе к сложным объектам, типа много подрешеточных сплавов. В этом случае особое значение приобретают вопросы структурной устойчивости выбранных моделей и типичность полученных результатов. Нетрудно получить, что энергия парного взаимодействия частиц между собой, вычисленные для одной РЭЯ и для всего кристалла с учетом бесконечного радиуса взаимодействия, будут иметь одинаковый вид. Исследования бинарных сплавов на основе структуры А2, упорядочивающейся со звездой сверхструктурного вектора {k10}, позволяют найти неравновесный термодинамический потенциал F(Р), определяющий поведение системы:
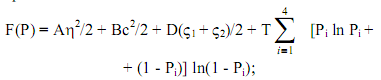
коэффициенты A, B, D являются линейными комбинациями энергетических параметров.
Конкретный вид этой зависимости определяется числом учитываемых в модели координационных сфер. Произвольно варьируя энергию парного взаимодействия можно достичь условий стабильности любой фазы, даваемой моделью с бесконечным радиусом взаимодействия.
Работа выполнена при поддержке РФФИ, грант № 02-02-17871.



