Задача исследований
Применение параллельной обработки данных в высокоскоростных системах управления приводит к усложнению и увеличению аппаратурных затрат. Для обеспечения высокой надежности функционирования таких систем целесообразно применять корректирующие коды.
Решение
Современные системы управления предъявляют высо-кие требования к скорости обработки данных. Особенно это ярко проявляется в области цифровой обработки сигналов (ЦОС). Для обеспечения ЦОС в реальном масштабе времени в работах [1,2,4] предложено использовать модулярные полиномиальные коды (МПК). В то же время высокие требования предъявляются к надежности работы всей системы, и, в частности, спецпроцессоров (СП) ЦОС.
В настоящее время одним из наиболее перспективных путей повышения надежности функционирования вычислительных устройств является применение корректирующих кодов.
Особое место среди модулярных полиномиальных кодов занимают коды полиномиальной системы классов вычетов (ПСКВ). Для обнаружения и исправления ошибок, возникающих в результате отказов элементов вычислительных трактов СП ПСКВ, целенаправленно вводится избыточность.
Согласно [1,3] если на диапазон возможного изменения кодируемого множества полиномов наложить ограничения, то есть выбрать k из п оснований ПСКВ (kполн (z) расширенного поля Галуа GF(pν) на два непересекающихся подмножества. Первое подмножество называется рабочим диапазоном и определяется выражением
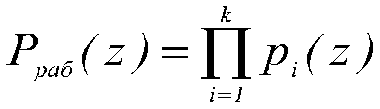 (1)
(1)
Многочлен a(z) с коэффициентами из поля GF(p) будет считаться разрешенным в том и только том случае, если он является элементом нулевого интервала полного диапазона P полн (z), то есть принадлежит рабочему диапазону a(z)∈P раб (z). Второе подмножество GF(pν), определяемое произведением r=n-k контрольных оснований
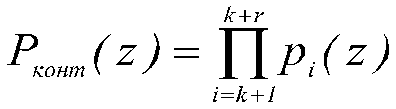 (2)
(2)
задает совокупность запрещенных комбинаций. Если a(z) является элементом второго подмножества, то считается, что данная комбинация содержит ошибку. Таким образом, местоположение полинома a(z) относительно подмножеств позволяет однозначно определить, является ли кодовая комбинация A(z)=(α1(z), α2(z),...αn(z)) разрешенной, или она содержит ошибочные символы.
Рассмотрим корректирующие способности кодов ПСКВ, с одним контрольным основанием. В упорядоченной системе оснований ПСКВ в качестве контрольного выбирается модуль, удовлетворяющий условно
![]()
Считаем, что если исходные операнды A(z)=(α1(z), α2(z),...α k+1(z)) и B(z)=(β1(z), β2(z),...β k+1(z)) как и результат выполнения ° арифметической операции C(z)=a(z)°B(z), лежат внутри диапазона pраб(z), то полином C(z)=(γ1(z), γ2(z),...γ k+1(z)) не содержит ошибки. В противоположном случае, результат C(z) является ошибочным. Для поиска местоположения ошибки в коде ПСКВ воспользуемся теоремой о распределении ошибки по полному диапазону системы.
Теорема. Если в ПСКВ с одним контрольным основанием p1(z), p2(z),..., pn(z), p n+1(z) задан неправильный полином A*(z)=(α1(z), ...,α*i(z),..., α n+1(z)) с искаженным по i-му основанию остатком, то номер интервала j в который попадет A*(z) определяется формулой
![]()
Доказательство. В соответствии с тем, что ошибочный полином A*(z) получен из разрешенного полинома a(z) в результате искажения остатка αi(z) по модулю pi (z), имеем
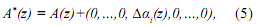
где ![]() -глубина ошибки
-глубина ошибки
Известно, что интервал распределения полинома A*(z), определяется следующим выражением
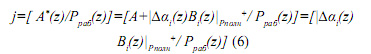
При этом справедливо, что
Тогда, подставив последние выражения в равенство (6), получаем
![]()
Теорема доказана.
Показжем, что искажение любого остатка выводит исходный полином a(z) из множества разрешенных комбинаций. Пусть задано поле Галуа GF(24), в котором определены рабочие основания p1(z)=z+1; p2(z)=z2+z+1; p3(z)=z4+z3+z2+z+1; p4(z)=z4+z3+1 и одно контрольное - p5(z)=z4+z+1. В этом случае pраб(z)=z11+z8+z7+z5+z3+z2+z+1, а ортогональные базисы bi (z) и их веса mi(z) равны
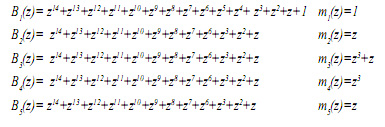
Пусть задан полином a(z)= z5+z4+1, принадлежащий рабочему диапазону. Тогда a(z)=(1,0, z3+z2+z+1,z+1,z2). Согласно (4) имеем
![]()
Пусть ошибка произошла по первому основанию. Представим искаженный полином A*(z) в позиционном виде
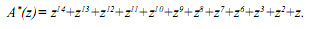
Тогда номер интервала, в который попал A*(z) равен
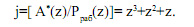
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов/ Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2005. 276 с.
- Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронных сетей для исследования ортогональных преобразований в расширенных полях Галуа/Нейрокомпьютеры: разработка, применение. №6, 2003. с.61-68.
- Калмыков И.А., Щелкунова Ю.О., Гахов В.Р., Шилов А.А. Математическая модель коррекции ошибок в полиномиальной системе класса вычетов на основе определения корней интервального полинома/Волновые процессы. №5, т.6, Самара, 2003 - С.30-34.
- Элементы применения компьютерной математики и нейроинформатики/Н.И. Червяков, И.А. Калмыков И.А., В.А. Галкина, Ю.О. Щелкунова, А.А. Шилов; Под ред. Н.И.Червякова. - М.: ФИЗМАТЛИТ, 2003. - 216с.



