Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

1. Введение

Под сплошной средой (пренебрегая её дискретным атомно-молекулярным строением) понимается практически вся окружающая нас среда.

Под прямыми задачами механики сплошной среды понимаются определение возмущений сплошной среды: перемещений, напряжений, деформаций, скоростей деформаций, наэлектризованность, намагниченность и т.п. под действием приложенных сил.

Под обратными задачами механики сплошной среды понимаются задачи определения структуры среды и действующих на неё сил по измеряемым, известным возмущениям сплошной среды.

Обратными задачами механики сплошных сред начали заниматься в 30-х годах прошлого столетия в связи с потребностью поиска полезных ископаемых и необходимостью неразрушающего контроля: определения работоспособности зданий, мостов и сооружений по измеряемым механическим величинам на доступной части сооружений.

Бурный рост теоретических исследований обратных задач и научно-технических разработок по их практическому приложению начался с середины 50-х годов прошлого столетия и продолжается по настоящее время.

Исследованию обратных задач посвящено большое количество статей, монографий и журналов.

По этим вопросам проводятся многочисленные международные конференции. Так, в апреле 2010 года в Китае прошла конференция по обратным задачам, в начале июня 2010 года прошла конференция в Турции, с 26 июня по 16 июля 2010 года проведена летняя школа в Вашингтоне. Полный перечень конференций по обратным задачам можно найти в Интернете.

В России бесспорным лидером по исследованию обратных задач (как в теоретическом плане, так и в плане практического использования) является Романов Владимир Гаврилович (г. Новосибирск).

Обратными задачами по океанологии в Ростовском государственном университете начали заниматься с 1982 г. в рамках хозяйственного договора с Морским Гидрофизическим Институтом (МГИ НАН Украины, г. Севастополь).

В связи с тем, что в НАН Украины под руководством академика Нелепо Б.А. стали использовать Искусственные Спутники Земли (ИСЗ) по наблюдению за проявлением внутренних волн на поверхности океана, стало возможным по этим проявлениям изучать внутреннюю структуру океана и распределение плотности по его глубине.

Мировой океан разбит на пятиградусные квадраты Марсдена и в каждом из них научными экспедициями в рамках ЮНЕСКО проведены исследования фонового распределения плотности океана. Результаты этих исследований хранятся в Международных Центрах Данных (МЦД) (один из них находится в России, в городе Обнинске).

При очередном наблюдении с ИСЗ по проявляемым на свободной поверхности фазовым характеристикам внутренних волн определяются аномалии распределения плотности в толще океана. Такие аномалии в распределении плотности могут создавать затонувшие суда, батискафы, косяки рыб, подлодки, аквалангисты и т.д.

2. История вопроса

Математически рассматриваемые обратные задачи сводятся к определению переменного коэффициента в дифференциальном операторе Штурма-Лиувилля по собственным числам этого оператора [1].

Первый существенный результат в данном направлении, по-видимому, был получен в 1929 г. В.А. Амбарцумяном. Он показал, что в общем случае без каких-либо условий оператор Штурма - Лиувилля определяется неоднозначно. В качестве одного из вариантов дополнительных условий он предложил использовать два спектра задачи Штурма - Лиувилля при различных граничных условиях. Затем Борг (1946) выполнил первое систематическое исследование обратной задачи для оператора Штурма - Лиувилля. Он показал, что в общем случае оператор Штурма-Лиувилля определяется по двум спектрам (при различных граничных условиях). Дальнейшие существенные успехи в теории обратных задач были достигнуты: Л.А. Чудовым (1949), В.А. Марченко (1952), М.Г. Крейном (1951), И.М. Гельфандом, Б.М. Левитаном (1951), М.Г. Гасымовым (1964), А.Н. Тихоновым (1963). Обзор теоретических работ по обратным задачам Штурма - Лиувилля приведен в [1].

В работе [2] указаны научно-технические методы определения структуры сред при их дистанционном зондировании.

Изучение толщи океана из космоса начало проводиться в Морском гидрофизическом институте АН Украины под руководством академика Нелепо Б.А. в конце 70-х годов прошлого столетия. В монографии [3] обобщены итоги важнейших исследований в этом направлении.

Реализация различных методов решения прямых и обратных спектральных задач волновых движений неоднородной жидкости в Мировом океане проведена в работе [4].

3. Океанологическая постановка задачи определения структуры Мирового океана

Ставится задача: по фазовым характеристикам внутренних волн, проявляемым на свободной поверхности, определить распределение плотности в толще океана для конкретного района Мирового океана [4]. Решение этой задачи проведем на основе общепринятой океанологической постановки задачи о свободных внутренних волнах во вращающейся системе координат (системе координат, связанной с поверхностью Земли) [5]:

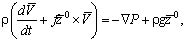
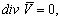
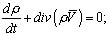   (1)

Здесь 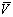 - вектор скорости в декартовой системе координат; P - отклонение гидродинамического давления от равновесного;  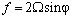- параметр Кориолиса (Ω - угловая скорость вращения Земли, φ - широта), P, ρ - отклонения давления и плотности жидкости от равновесных P₀, ρ₀, g - ускорение свободного падения,  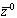- орт, направленный по оси z (против силы тяжести вертикально вверх).

На дне 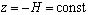 выполняется условие непротекания, на свободной поверхности океана выполняются кинематические и динамические граничные условия:

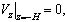
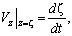
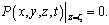  (2)

Далее система (1) и граничные условия (2) линеаризируются и решение ищется в виде бегущих волн:

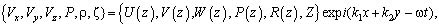 (3)

здесь k₁, k₂ - волновые числа, ω - частота колебаний по времени.

После преобразований рассматриваемая задача сводится к спектральной задаче относительно амплитудной функции вертикальной компоненты скорости частиц жидкости.

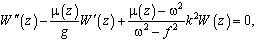(4)

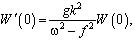
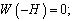(A):    (B):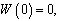  

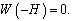
Здесь 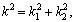 W(z) - амплитудная функция вертикальной компоненты скорости частиц жидкости, µ(z) - квадрат частоты плавучести (частоты Вяйсяля-Брента),

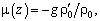(5)

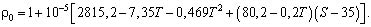
Входящие в (5) величины T и S представляют собой температуру и солёность, определяемые на основе натурных измерений [4].

Условия (А) являются полными краевыми условиями и не отделяют поверхностные волны от внутренних. Условия (В) соответствуют приближению «твердой крышки» и осуществляют фильтрацию внутренних волн от поверхностных.

В прямой спектральной задаче по функции µ(z), вычисленной на основе обработки экспериментальных данных для T и S, строятся зависимости ω(k) (дисперсионные кривые) для фоновых колебаний изучаемого района Мирового океана.

В обратной спектральной задаче для внутренних волн по известным дисперсионным зависимостям ω(k) восстанавливается функция µ(z). Найденная на основе решения обратной задачи функция µ(z) сравнивается с фоновым распределением частоты плавучести (частоты Вяйсяля-Брента) и по её отклонениям от фоновой определяются возмущения плотности в данном районе океана.

4. Методы решения обратных спектральных задач механики сплошных сред [4, 6-8, 11].

В [4] предложены как прямые численные методы решения обратных океанологических задач, так и асимптотические. А именно, используются ВКБ-асимптотики, метод сращиваемых асимптотических разложений, асимптотический метод при наличие точек поворота. В асимптотических методах для прямой задачи строятся в аналитическом виде законы дисперсии. На основе этих аналитических зависимостей определяется характер неоднородности среды, так же в аналитическом виде, что позволяет исследовать зависимость точности решения обратной задачи от точности входной (измеряемой) информации.

В [4] приведено сведение исходной спектральной задачи к отысканию собственных чисел интегрального уравнения с симметричным, положительно определённым ядром.

С помощью теоремы Мерсера о первом следе интегрального уравнения найдена аналитическая зависимость неоднородности среды от собственных чисел.

Изложенные в [4] методы решения обратных спектральных задач волновых движений стратифицированного Мирового океана применимы и для решения обратных задач в других областях механики сплошных сред [6-8, 11].

В частности, рассмотрим задачу об определении неоднородности упругого слоя по резонансным частотам его антиплоских колебаний.

5. Определение плотности упругого слоя по резонансным частотам антиплоских колебаний [6]

Рассмотрим упругий слой толщины Н = const, закрепленный на обеих границах z = 0 и z = H и простирающийся до бесконечности по горизонтальным направлениям, начало координат берется на нижнем основании слоя, ось z направлена вертикально вверх, оси x, y - горизонтально.

В общем случае краевая задача состоит из основных уравнений теории упругости, записанных в перемещениях, и граничных условий [9]:

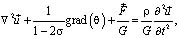
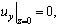
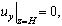   (6)

где 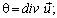 (x, y, z) - декартова система координат;  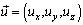- вектор перемещений; 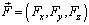- объемная сила; G = const - модуль сдвига, σ - коэффициент Пуассона, ρ(z) - плотность материала.

Предположим, что выполняются следующие условия:

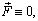
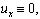
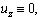
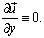     (7)

Тогда получим, что первое и третье уравнение системы (6) удовлетворяются тождественно, а второе уравнение и соответствующее ему граничное условие примут следующий вид:

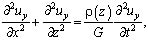
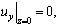
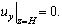  (8)

Ищем решение задачи о свободных антиплоских колебаниях в виде бегущих волн:

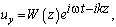
где ω - частота колебаний,

k - волновое число.

Обозначая ρ(z)/G через µ(z), получим краевую задачу:

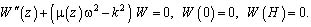 (9)

6. Определение физических и геометрических неоднородностей упругого стержня по резонансным частотам при его продольных, или крутильных колебаниях

Рассмотрим задачу о продольных колебаниях стержня с переменным сечением [10].

Здесь  - продольное смещение точек стержня;

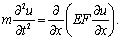 (10)

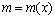 - масса единицы длины стержня, 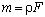;  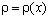- распределенная вдоль стержня плотность материала;  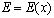- модуль Юнга;  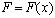- площадь поперечного сечения.

Ищем решение, периодическое по времени

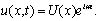 (11)

Тогда для амплитудной функции U(x) имеем уравнение

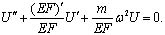 (12)

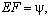
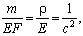
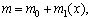
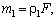
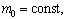
Введем обозначения:      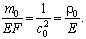   Здесь c = с(x) - местная скорость звука для произвольной плотности ρ(x) и произвольном модуле Юнга E(x); c₀ = с(x) - местная скорость звука для постоянной плотности  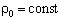и произвольном модуле Юнга E(x); m₁(x) - отклонение массы от постоянной; ρ₀(x) - отклонение плотности от постоянной.

При помощи замены:

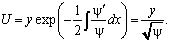
Сведём уравнение (12) к виду:

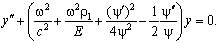 (13)

Граничные условия возьмём в виде

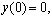
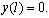  (14)

Здесь l является длиной стержня. Сделав замену 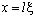, из выражений (13), (14) выводим краевую задачу для :

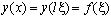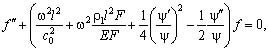(15)

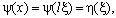
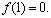
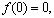
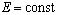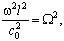
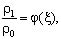
Рассмотрим частный случай . Обозначив  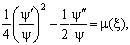    выпишем окончательную краевую задачу для функции f .

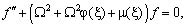 (16)

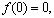
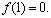
В случае крутильных колебаний упругого стержня дифференциальное уравнение для угла закручивания имеет тот же вид, что и для продольных колебаний (10). Поэтому геометрическая и физическая неоднородности стержня определяются по резонансным частотам крутильных колебаний стержня, так же, как и по резонансным частотам продольных колебаний [7].

7. Определение физической и геометрической неоднородности стержня по резонансным частотам
его изгибных колебаний [8, 11]

В линейной постановке рассмотрим задачу об изгибных колебаниях шарнирно опертого стержня, продольно нагруженного силой p(x) [10]:

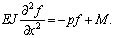 (17)

здесь f - прогиб стержня; E = E(x) - модуль Юнга; J = J(x) - момент инерции поперечного сечения относительно нейтральной оси; M - изгибающий момент относительно главной центральной оси за счет других сил, помимо продольных p(x). Ось Ox направлена вдоль оси стержня.

Продифференцировав уравнение (17) дважды по x, получим [10]:

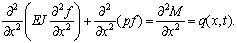 (18)

здесь q(x, t) - распределенная нагрузка, действующая на стержень. При отсутствии внешней активной распределенной нагрузки силы инерции 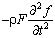 являются распределенной нагрузкой [10]. Здесь  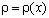- плотность материала;  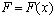- площадь поперечного сечения стержня; t - время.

Тогда из (17) следует:

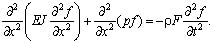(19)

Граничные условия при шарнирном опирании имеют вид [10]:

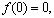
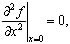
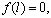
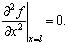     (20)

Начало координат взято на левом конце балки.

Решение уравнения (19) ищем в виде:

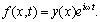(21)

Тогда для функции y(x) получаем следующую краевую задачу [10]:

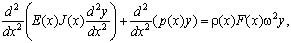(22)

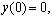
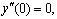
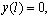
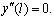
Числа 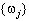, i = 1, 2, ..., доставляющие ненулевое решение однородной краевой задаче (22) и будут резонансными частотами изгибных колебаний неоднородного стержня. В общем случае неоднородность стержня обуславливается геометрической неоднородностью (J(x), F(x)), физической (E(x), ρ(x)), и неоднородностью продольной силы p(x).

Теми же методами, которые предложены при решении обратной спектральной океанологической задачи, решаются обратные спектральные задачи (9), (16), (22). А именно, по известным резонансным частотам восстанавливаются физические и геометрические неоднородности упругих сред.

СПИСОК ЛИТЕРАТУРЫ

1. Левитан Б.М. Обратные задачи Штурма-Лиувилля. - М.: Наука, 1967. - 240 с.
2. Волкова Е.А. Потетюнко Э.Н. Обзор научно-технических разработок по обнаружению скрытых объектов // Современные наукоёмкие технологии. - М.: «Академия естествознания», 2009. - №9. - С. 132-134.
3. Нелепо Б.А., Коротаев Г.К., Суетин В.С., Терехин Ю.В. Исследование океана из космоса. - Киев: Наукова думка, 1985. - 168 с.
4. Потетюнко Э.Н., Черкесов Л.В., Шубин Д.С., Щербак Е.Н. Свободные колебания и обратные спектральные задачи. - М.: Вузовская книга, 2001. - 288 с.
5. Миропольский Ю.З. Динамика внутренних гравитационных волн в океане. - Л.: Гидрометеоиздат, 1981. - 302 с.
6. Ekaterina Anosova, Issac Herskowitz, Edward N. Potetyunko Assesssment of the Efficiency of the Structure Foundation by the Resonance Frequencies of its Anti Planar Vibrations // Proceedings of the 2005 Structures Congress and the 2005 Forensic Engineering Symposium. - New York, 2005.
7. Потетюнко Э.Н., Щербак Е.Н. The inverse spectral problem in the detektioen of the defect end heteroge // Eneititles os the civil engeneering. - С. 1-10. - Мехико, Jolu 12-15. - 2005.
8. ANOSOVA Ye. A. (1); POTETUNKO E. N. (1) ; SCHERBAK Ye. N. (2) ; Journal of Engineering Mathematics (2006) 55: 339-356 Springer 2006 DOI 10.1007/s10665-006-9032-7.
9. НовацкийВ. Теория упругости. - М.: Изд-во «Мир», 1975. - 872 с.
10. Бидерман В.Л. Прикладная теория механических колебаний. Учеб. пособие для втузов. - М.: Высшая школа, 1972. - 416 с.
11. Величко А.С., Потетюнко Э.Н., Щербак Е.Н. Обратные задачи свободных колебаний стержней // Деп. в ВИНИТИ №39-В2004 - Ростов-на-Дону: РГУ, 2004. - 116 с.