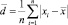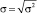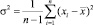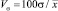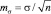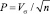Динамика – это изменение во времени [3–5]. Для родника динамическими показателями являются время наполнения емкости и расход водотока, вычисляемый как отношение объема мерного сосуда к времени его наполнения.
Эксперименты проводили в местности, которая богата родниками, в так называемом «родниковом крае». Действительно, Куженерский район можно назвать настоящим родниковым краем [2]. Проходящий по территории района Вятский увал создает уникальное движение подземных вод на своих склонах, из-за чего в этих местах много источников, ключей ручьев. На территории поселка Куженер находится немало мелких родников.
Одним из них является «Хрустальная ель», родник находится в долине реки Немда, под Якайсуртом в овраге. Его кристально-чистая вода по душе многим жителям.
Ключ бьёт из-под корней ели и образует несколько ручейков. Сам родник представляет собой небольшой ключ, который под напором выходит из земли в специальном углублении. Вместе с подземными выходами образуется некая система водотоков в роднике, которая собирается в деревянном лотке и вытекает в нескольких крупных струях.
Устойчивые законы. По принципу «от простого к сложному» в таблице 1 предложены «кирпичики» для построения, по ходу структурно-параметрической идентификации биотехнического закона [3, 5], искомой закономерности.
При моделировании временных рядов тренд нужно вначале искать по закону экспоненциального роста или гибели (спада). Тренды во времени всегда имеют предысторию, так как ничто не возникает в историческом поведении на пустом месте, то есть с нуля. Тенденции по структурной динамике вполне могут начаться с нулевого элемента системы, т.е. в новых условиях. Все шесть устойчивых законов распределения из таблицы 1 являются частными случаями биотехнического закона, показанного в нижней строке.
Уровни коэффициента корреляции. Теперь можно определиться с уровнями коэффициента корреляции. Это позволит затем ранжировать полученные по функциональным факторным связям по тесноте коррелятивной вариации (термин по Ч. Дарвину).
Таблица 1
Математические конструкты для построения статистической модели [5]
|
Фрагменты без предыстории изучаемого явления или процесса |
Фрагменты с предысторией изучаемого явления или процесса |
|
y = ax – закон линейного роста или спада (при отрицательном знаке перед правой стороной приведенной формулы) |
y = a – закон не влияния принятой переменной на показатель, который имеет предысторию значений |
|
y = axb – закон показательного роста (закон показательной гибели y = ax–b не является устойчивым, из-за бесконечности при нулевом значении объясняющей переменной |
y = a exp(±cx) – закон Лапласа (Ципфа в биологии, Парето в экономике, Мандельброта в физике) экспоненциального роста или гибели, относительно которого создан метод операторных исчислений |
|
y = axb(–cx) – биотехнический закон в упрощенной форме |
y = a exp(±cxd) – закон экспоненциального роста или гибели, – по проф. П.М. Мазуркину |
|
y = axb(–cxd) – биотехнический закон – проф. П.М. Мазуркин |
|
Всего рассмотрим восемь уровней адекватности полученной после идентификации закономерности, начиная от коэффициента корреляции, равного 0,000. При этом для научно-технического творчества особо рекомендуются к вниманию зависимости с корреляцией от 0,300 до 0,500. Их считают слабыми связями и, не задумываясь, отбрасывают.
Но, в других условиях функционирования, именно слабые по результатам текущих наблюдений и прошлых экспериментов в будущем могут стать сильными.
Таблица 2
Коэффициент корреляции между факторами
|
Интервал коэффициента корреляции |
Характер тесноты связи |
|
|
Существующая классификация |
Предлагаемая классификация |
|
|
1,0000 |
сильная связь |
однозначная |
|
0,9000…1,0000 |
сильнейшая |
|
|
0,7000…0,9000 |
сильная |
|
|
0,500…0,700 |
слабая связь |
средняя |
|
0,300...0,500 |
слабоватая |
|
|
0,100…0,300 |
нет связи |
слабая |
|
0,000…0,100 |
слабейшая |
|
|
0,000 |
нет связи |
|
Летом 2012 года нами проведен мониторинг расхода воды на малом водотоке в роднике «Хрустальная Ель». Все данные по результатам эксперимента представлены в табл. 3. Методика в основном та же, что и для предыдущего эксперимента. Отличие заключается в том, что мерный сосуд был ковшом в один литр.
Все измерения проводились вечером с 17-00 часов. Поэтому текущее время τ берется целыми сутками. Расход малого водотока q взяли в размерности мл/c, т.к. в размерности л/с значения объемного расхода были значимыми для крупного водотока и были слишком малыми по числам для мелкого по расходу водотока родника.
Для моделирования в программной среде CurveExpert соотношения чисел на осях абсцисс и ординат должны быть соразмерными. Продолжительность в 76 суток достаточна, чтобы выявлять к тренду волновые закономерности возмущения изучаемого признака.
Ранее измерения большого водотока получились неточными. Большой водоток требует быструю реакцию или автоматическую регистрацию. Не соблюдая такие условия, может возникнуть большая погрешность при измерении крупного водотока.
На рис. 1 показано фото места истечения одного малого водотока.
Расход в нем слишком мал, поэтому за мерное устройство приняли ковш объемом в один литр. И его было достаточно, чтобы мерный сосуд наполнялся не менее чем за 15 секунд (расчеты и обоснование погрешности измерений приведены в седьмой главе). Если для наполнения мерного сосуда времени требуется больше, то значит, при ручной фиксации времени секундомером результаты измерений будут также точнее.
Таблица 3
Результаты измерений расхода воды малого водотока из родника «Хрустальная ель»
|
№ п/п |
Дата |
Время измерения τ, сутки |
Время наполнения T, с |
Расход q, л/с |
Расход q, мл/с |
№ п/п |
Дата |
Время измерения τ, сутки |
Время наполнения T, с |
Расход q, л/с |
Расход q, мл/с |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
1 |
23.07.12 |
0 |
57.38 |
0,0174 |
17,4 |
66 |
12 |
70.43 |
0,0142 |
14,2 |
|
|
2 |
17-00 |
0 |
56.68 |
0,0176 |
17,6 |
67 |
12 |
69.75 |
0,0143 |
14,3 |
|
|
3 |
0 |
54.32 |
0,0184 |
18,4 |
68 |
12 |
68.11 |
0,0147 |
14,7 |
||
|
4 |
0 |
63.26 |
0,0158 |
15,8 |
69 |
12 |
74.40 |
0,0134 |
13,4 |
||
|
5 |
0 |
59.28 |
0,0169 |
16,9 |
70 |
12 |
72.45 |
0,0138 |
13,8 |
||
|
6 |
0 |
52.08 |
0,0192 |
19,2 |
71 |
6.08.12 |
14 |
70.59 |
0,0142 |
14,2 |
|
|
7 |
0 |
65.92 |
0,0152 |
15,2 |
72 |
14 |
68.79 |
0,0145 |
14,5 |
||
|
8 |
0 |
63.18 |
0,0158 |
15,8 |
73 |
14 |
72.10 |
0,0139 |
13,9 |
||
|
9 |
0 |
69.12 |
0,0145 |
14,5 |
74 |
14 |
76.38 |
0,0131 |
13,1 |
||
|
10 |
0 |
65.27 |
0,0153 |
15,3 |
75 |
14 |
72.67 |
0,0138 |
13,8 |
||
|
11 |
24.07.12 |
1 |
61.99 |
0,0161 |
16,1 |
76 |
14 |
70.12 |
0,0143 |
14,3 |
|
|
12 |
17-00 |
1 |
65.52 |
0,0153 |
15,3 |
77 |
14 |
74.93 |
0,0133 |
13,3 |
|
|
13 |
1 |
72.20 |
0,0139 |
13,9 |
78 |
14 |
75.35 |
0,0133 |
13,3 |
||
|
14 |
1 |
70.84 |
0,0141 |
14,1 |
79 |
14 |
70.43 |
0,0142 |
14,2 |
||
|
15 |
1 |
69.97 |
0,0143 |
14,3 |
80 |
14 |
72.02 |
0,0139 |
13,9 |
||
|
16 |
1 |
70.71 |
0,0141 |
14,1 |
81 |
15.08.12 |
23 |
77.34 |
0,0129 |
12,9 |
|
|
17 |
1 |
74.03 |
0,0135 |
13,5 |
82 |
23 |
86.22 |
0,0116 |
11,6 |
||
|
18 |
1 |
72.67 |
0,0138 |
13,8 |
83 |
23 |
83.31 |
0,0120 |
12 |
||
|
19 |
1 |
75.86 |
0,0132 |
13,2 |
84 |
23 |
85.79 |
0,0117 |
11,7 |
||
|
20 |
1 |
75.63 |
0,0132 |
13,2 |
85 |
23 |
81.20 |
0,0123 |
12,3 |
||
|
21 |
1 |
72.19 |
0,0139 |
13,9 |
86 |
23 |
86.96 |
0,0115 |
11,5 |
||
|
22 |
25.07.12 |
2 |
73.78 |
0,0136 |
13,6 |
87 |
23 |
80.43 |
0,0124 |
12,4 |
|
|
23 |
2 |
73.01 |
0,0137 |
13,7 |
88 |
23 |
78.40 |
0,0128 |
12,8 |
||
|
24 |
2 |
75.87 |
0,0132 |
13,2 |
89 |
23 |
82.25 |
0,0122 |
12,2 |
||
|
25 |
2 |
73.90 |
0,0135 |
13,5 |
90 |
23 |
89.20 |
0,0112 |
11,2 |
||
|
26 |
2 |
75.97 |
0,0132 |
13,2 |
91 |
13.09.12 |
52 |
105.00 |
0,0095 |
9,5 |
|
|
27 |
2 |
77.32 |
0,0129 |
12,9 |
92 |
52 |
105.73 |
0,0095 |
9,5 |
||
|
28 |
2 |
75.27 |
0,0133 |
13,3 |
93 |
52 |
101.49 |
0,0099 |
9,9 |
||
|
29 |
2 |
71.12 |
0,0141 |
14,1 |
94 |
52 |
103.47 |
0,0097 |
9,7 |
||
|
30 |
2 |
71.88 |
0,0139 |
13,9 |
95 |
52 |
100.87 |
0,0099 |
9,9 |
||
|
31 |
2 |
66.06 |
0,0151 |
15,1 |
96 |
52 |
106.29 |
0,0094 |
9,4 |
||
|
32 |
26.07.12 |
3 |
76.65 |
0,0130 |
13 |
97 |
52 |
104.50 |
0,0096 |
9,6 |
|
|
33 |
3 |
77.35 |
0,0129 |
12,9 |
98 |
52 |
104.41 |
0,0096 |
9,6 |
||
|
34 |
3 |
70.65 |
0,0142 |
14,2 |
99 |
52 |
102.51 |
0,0098 |
9,8 |
||
|
35 |
3 |
69.72 |
0,0143 |
14,3 |
100 |
52 |
103.22 |
0,0097 |
9,7 |
||
|
36 |
3 |
65.01 |
0,0154 |
15,4 |
101 |
14.09.12 |
53 |
104.59 |
0,0096 |
9,6 |
|
|
37 |
3 |
63.69 |
0,0157 |
15,7 |
102 |
53 |
102.02 |
0,0098 |
9,8 |
||
|
38 |
3 |
75.69 |
0,0132 |
13,2 |
103 |
53 |
100.43 |
0,0100 |
10 |
||
|
39 |
3 |
71.15 |
0,0141 |
14,1 |
104 |
53 |
105.35 |
0,0095 |
9,5 |
||
|
40 |
3 |
73.41 |
0,0136 |
13,6 |
105 |
53 |
100.93 |
0,0099 |
9,9 |
||
|
41 |
3 |
71.41 |
0,0140 |
14 |
106 |
53 |
102.43 |
0,0098 |
9,8 |
||
|
42 |
27.07.12 |
4 |
74.11 |
0,0135 |
13,5 |
107 |
53 |
103.25 |
0,0097 |
9,7 |
|
|
43 |
4 |
73.25 |
0,0137 |
13,7 |
108 |
53 |
103.78 |
0,0096 |
9,6 |
||
|
44 |
4 |
71.20 |
0,0140 |
14 |
109 |
53 |
105.02 |
0,0095 |
9,5 |
||
|
45 |
4 |
70.93 |
0,0141 |
14,1 |
110 |
53 |
104.12 |
0,0096 |
9,6 |
||
|
46 |
4 |
74.98 |
0,0133 |
13,3 |
111 |
6.10.12 |
75 |
106.35 |
0,0094 |
9,4 |
|
|
47 |
4 |
70.43 |
0,0142 |
14,2 |
112 |
75 |
108.40 |
0,0092 |
9,2 |
||
|
48 |
4 |
69.75 |
0,0143 |
14,3 |
113 |
75 |
108.79 |
0,0092 |
9,2 |
||
|
49 |
4 |
68.11 |
0,0147 |
14,7 |
114 |
75 |
109.10 |
0,0092 |
9,2 |
||
|
50 |
4 |
74.40 |
0,0134 |
13,4 |
115 |
75 |
107.64 |
0,0093 |
9,3 |
||
|
51 |
28.07.12 |
5 |
72.45 |
0,0138 |
13,8 |
116 |
75 |
108.21 |
0,0092 |
9,2 |
|
|
52 |
5 |
70.59 |
0,0142 |
14,2 |
117 |
75 |
108.07 |
0,0093 |
9,3 |
||
|
53 |
5 |
68.79 |
0,0145 |
14,5 |
118 |
75 |
109.15 |
0,0092 |
9,2 |
||
|
54 |
5 |
72.10 |
0,0139 |
13,9 |
119 |
75 |
107.19 |
0,0093 |
9,3 |
||
|
55 |
5 |
76.38 |
0,0131 |
13,1 |
120 |
75 |
107.29 |
0,0093 |
9,3 |
||
|
56 |
5 |
72.67 |
0,0138 |
13,8 |
121 |
7.10.12 |
76 |
108.49 |
0,0092 |
9,2 |
|
|
57 |
5 |
70.12 |
0,0143 |
14,3 |
122 |
76 |
108.25 |
0,0092 |
9,2 |
||
|
58 |
5 |
74.93 |
0,0133 |
13,3 |
123 |
76 |
108.48 |
0,0092 |
9,2 |
||
|
59 |
5 |
75.35 |
0,0133 |
13,3 |
124 |
76 |
109.03 |
0,0092 |
9,2 |
||
|
60 |
5 |
70.48 |
0,0142 |
14,2 |
125 |
76 |
108.72 |
0,0092 |
9,2 |
||
|
61 |
4.08.12 |
12 |
74.11 |
0,0135 |
13,5 |
126 |
76 |
108.81 |
0,0092 |
9,2 |
|
|
62 |
12 |
73.25 |
0,0137 |
13,7 |
127 |
76 |
107.97 |
0,0093 |
9,3 |
||
|
63 |
12 |
71.20 |
0,0140 |
14 |
128 |
76 |
107.95 |
0,0093 |
9,3 |
||
|
64 |
12 |
70.93 |
0,0141 |
14,1 |
129 |
76 |
108.81 |
0,0092 |
9,2 |
||
|
65 |
12 |
74.98 |
0,0133 |
13,3 |
130 |
76 |
109.12 |
0,0092 |
9,2 |

Рис. 1. Малый водоток родниковой воды
В табл. 4 представлены значения показателей вариации, рассчитанные по формулам описательной статистики. Данные обрабатывались в программной среде Ecxel.
Показатель расхода воды имеет относительно высокий коэффициент вариации, но всё же не соблюдается общеизвестное условие 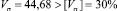 .
.
Это означает, что есть достаточно высокая погрешность усреднения статистической выборки. При этом среднее арифметическое значение определено надежно и этому свидетельствует показатель точности P = 3,92 %.
Таблица 4
Статистические параметры расхода воды эксперимента
|
Статистические показатели |
Формула |
Результат расчета |
|
Количество наблюдений, шт. |
n |
130 |
|
Размах R, мл/с |
R = xmax – xmin |
10 |
|
Минимум xmin, мл/с |
Выбор из ряда данных |
9,2 |
|
Максимум xmax , мл/с |
Выбор из ряда данных |
19,2 |
|
Среднее арифметическое |
|
12,604 |
|
Ср. линейное отклонение |
|
0,000154 |
|
Ср. квадратичное отклонение |
|
5,631 |
|
Коэффициент вариации Vσ, % |
|
44,68 |
|
Ср. ошибка выборки mσ |
|
0,49 |
|
Показатель точности P, % |
|
3,92 |
В связи с этим следует выполнить статистическое моделирование, а по измеренным параметрам малого водотока можно выявлять биотехнические закономерности с коэффициентом корреляции выше 0,9.
По точкам в окне программной среды сразу же видно, что изменение времени наполнения T в зависимости от текущего времени τ с начала эксперимента происходит волнообразно. В таком случае нужно определить тренд (тенденцию). Эксперимент в 76 суток оказался недостаточным по продолжительности для моделирования экспоненциального закона.
В связи с этим остается идентифицировать наипростейшую формулу закона не влияния, то есть конструкцию вида 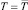 среднего арифметического значения (рис. 2 и 3).
среднего арифметического значения (рис. 2 и 3).
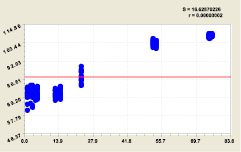
Рис. 2. График среднего арифметического значения времени наполнения
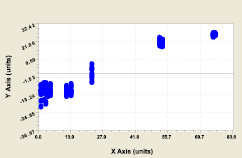
Рис. 3. Остатки после модели (1)
Вначале была получена простейшая формула
T = 82,44115. (1)
Далее была идентифицирована простая формула косинуса с постоянными параметрами модели. Запись волнового возмущения приобретает вид формулы
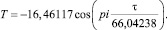 (2)
(2)
Отрицательный знак показывает кризисный характер колебательного возмущения. В знаменателе находится число 66,04238 половины периода колебательного значения. Весь период равен примерно 132 сутки. Частота колебания будет равна 132 или 1/132.
В этой модели половина амплитуды колебательного процесса равна 16,46117, а число π принимается символом pi в программе CurveExpert-1.3 с 18 знаками после запятой. Полупериод равен примерно 66 суток, то есть период колебания ожидается 132 сутки. Однако остатки после формулы (2) позволяют усложнить конструкцию статистической модели (2). Дополним постоянную амплитуду экспоненциальным законом, то есть введем функцию экспоненты.
Тогда можем дальше записать формулу так:
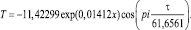 (3)
(3)
После усложнения конструкции модели амплитуда изменяется по устойчивому закону экспоненциального роста, аналогично сложную зависимость может иметь и период колебательного изменения. Но начало волны по формуле (3) не совпадает с началом координат при условии τ = 0. Поэтому сдвиг начала волны колебательного возмущения учитывается дополнительным параметром модели, помещаемым внутри функции косинуса, и получимформулу:
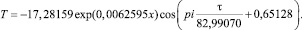 (4)
(4)
В этой формуле число 0,65128 показывает сдвиг начала волны относительно начала координат. Этот сдвиг измеряется в радианах.
Остатки после формулы (4) показали, что полупериод колебания является непостоянным. Поэтому усложняем конструкцию волновой функции. Повторная идентификация дает формулу
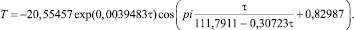 (5)
(5)
Формулу (5) можно записать в другом виде:
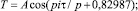 (5а)
(5а)
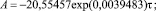
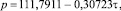
где A – амплитуда (половина) колебания, с; p – период (половина) колебания, сутки.
Полупериод колебания в начале эксперимента, то есть 23.07.12, был равен 111,8 суток, но затем он уменьшается. Это происходит потому, что летом характерна стабильная погода, а к осени влажность и температура атмосферного воздуха сильно и часто колеблется (рис. 4).
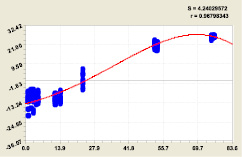
Рис. 4. Динамика времени наполнения
После следующего сеанса идентификации с усложнением конструкции программная среда дает аварийный останов. Поэтому окончательная модель приобретает вид формулы (5).
Теперь нужно соединить тренд (1) с волновой функцией (5) и получить общую закономерность:
T = T1 + T2; (6) (6)
T1 = 76,56800;
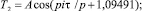
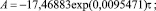
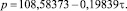
Далее усложним первую составляющую тем, что постоянный член дополним экспонентой. После идентификации получена формула
T = T1 + T2; (7)
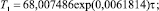
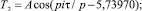
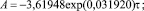
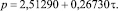
Первая составляющая стала законом экспоненциального роста. Вторая составляющая осталась кризисной, но по сравнению с формулой (5) изменилась конструкция полупериода: она стала возрастающей. Частота колебания уменьшается, т.е. время наполнения успокаивается.
Далее формулу (7) доведем до полноты конструкции (рис. 5, 6) в виде
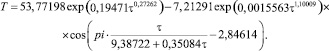 (8)
(8)
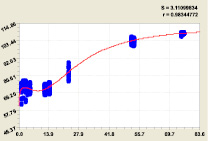
Рис. 5. Динамика времени наполнения ковшика в 1 л малым водотоком
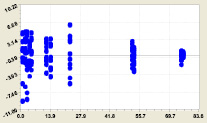
Рис. 6. Остатки от модели (8)
Готовая модель образует две составляющие, которые четко характеризуют волновое возмущение наполнения ковша водой родником. Первая составляющая являются известным законом экспоненциального роста при интенсивности роста 0,27262, а вторая – волновое возмущение с переменными амплитудой и частотой колебания.
По приведенной методике моделирования была приведена идентификация закономерностей по расчетному расходу малого водотока.
Кратко эта методика содержит следующие процедуры:
1) выявление постоянного члена, то есть тренда в виде среднего арифметического значения;
2) по остаткам от постоянного члена, усложняя конструкцию модели, идентифицируется волновая функция;
3) постоянный член совмещается с волновой функцией;
4) усложняется конструкция тренда (постоянного члена) до полной первой составляющей, т.е. до устойчивого не волнового закона.
На основе этой методики была получена (рис. 7 и 8) модель
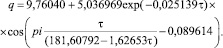 (9)
(9)
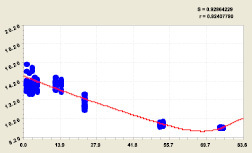
Рис. 7. Динамика расхода водотока
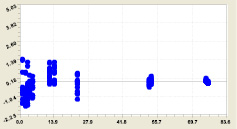
Рис. 8. Остатки от модели (9)
Оказалось, что первый член формулы (9) является постоянным. Это также объясняется относительно недостаточной продолжительностью эксперимента.
Коэффициент корреляции модели (9) равен 0,9241, что указывает на сильнейшую факторную связь. Чтобы объективно доказать волновой характер изменения расхода воды, необходимо добиться ламинарного потока жидкости. Крупный водоток сильно пульсирует, а малый водоток, как правило, является ламинарным.
Кроме того, время наполнения ковшика постоянной емкости, например, в один литр, значительное и это позволяет уменьшить погрешности измерения секундомером. Поэтому на одном малом водотоке нужно продолжить измерения в течение нескольких месяцев.
Для измерения расхода воды от водотоков разной мощности у одного и того же родника для ориентировочного анализа водотоков применяют мерные сосуды такой емкости, чтобы они заполнялись не быстрее пять секунд. Тогда, при реакции человека по 0,3 с на включение и отключение секундомера, погрешность измерений времени наполнения составит 0,6 с. Измерения будут проведены с общей погрешностью измерений не более 100∙0,6/5 = 12 %.
С учетом времени взятия пробы, сезонности и особенностей рельефа [1] можно будет составлять исходные данные для изучения влияния орографических факторов местности и количества осадков в виде дождя и снега на удельный расход воды родником. Это позволит выявлять биотехнические закономерности влияния лесов и растительного покрова в целом, а также ведения сельскохозяйственных и иных работ вокруг родников, на окружающую среду и учет антропогенного влияния на расход воды в сети родников.




 , мл/с
, мл/с
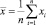
 , мл/с
, мл/с