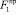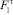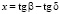Явление косого гидравлического прыжка возникает в бурном потоке, когда его струи относительно резко отклоняются на конечный угол внутрь потока [1]. Внешне косой прыжок проявляется в резком, почти скачкообразном повышении свободной поверхности. Фронт прыжка представляет собой полосу конечной ширины, но, учитывая ее относительно небольшую величину, прыжок схематически обозначается уступом (рис. 1).

Рис. 1. Сечение потока в направлении, перпендикулярном фронту прыжка
Для изучения двухмерных в плане бурных потоков можно использовать законы «масса – количество движения», так как они применимы как к неразрывным, так и к разрывным условиям течения потока, а законы «масса – энергия» применимы только к потокам с непрерывными параметрами течения.
В настоящей работе, пользуясь парой уравнений «масса – количество движения», определим основные параметры косого гидравлического прыжка и оценим падение напора в интеграле энергии.
Этими вопросами занимался Б.Т. Емцев [1, 2], который вывел следующие зависимости:
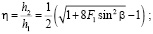 (1)
(1)
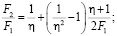 (2)
(2)
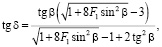 (3)
(3)
где 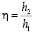 – относительная высота прыжка; F1 – число Фруда перед прыжком; F2 – число Фруда после прыжка; b – угол, характеризующий направление фронта гидравлического прыжка; d – угол набегания потока на боковую стенку русла.
– относительная высота прыжка; F1 – число Фруда перед прыжком; F2 – число Фруда после прыжка; b – угол, характеризующий направление фронта гидравлического прыжка; d – угол набегания потока на боковую стенку русла.
Считая известными величины 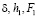 , по формулам (1) – (3) необходимо определить параметры
, по формулам (1) – (3) необходимо определить параметры 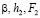 .
.
Б.Т. Емцев построил номограмму косых гидравлических прыжков [1], которую необходимо использовать для определения угла 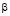 в уравнении (3). Однако её использование вызывает определённые неудобства, к тому же значения угла набегания на стенку в таблице ограничены значением 60°, а на практике угол растекания потока, например, за круглыми трубами может значительно превышать 60°, следовательно использовать номограмму из [1], с. 114 невозможно.
в уравнении (3). Однако её использование вызывает определённые неудобства, к тому же значения угла набегания на стенку в таблице ограничены значением 60°, а на практике угол растекания потока, например, за круглыми трубами может значительно превышать 60°, следовательно использовать номограмму из [1], с. 114 невозможно.
В связи с этим в настоящей работе разработан численно-аналитический метод решения уравнения (3) с применением прикладных математических пакетов Maple 9.5.
Выразив sinb через tgb, перепишем уравнение (3) в форме
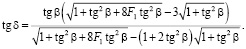 (4)
(4)
Избавимся в (4) от радикалов, преобразовав его к виду:
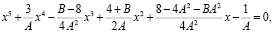 (5)
(5)
где 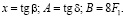
Преобразуем уравнение (5) к виду, содержащему параметр F1 [3]:
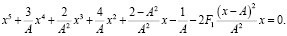 (6)
(6)
Сделаем замену переменной
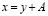 . (7)
. (7)
После замены (7) из уравнения (6) получим
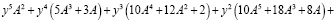
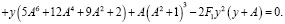 (8)
(8)
Опуская математические преобразования, приведем формулу для предельного значения критерия Фруда F1 при котором уравнение (7) имеет единственный положительный корень
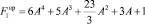 . (9)
. (9)
В табл. 1 приведены для сравнении расчетные значения предельного значения критерия Фруда 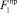 и значения Фруда, взятые из номограмм Б.Т. Емцева
и значения Фруда, взятые из номограмм Б.Т. Емцева 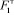 .
.
Таблица 1
Сравнение расчетных предельных значений Фруда и по номограмме Б.Т. Емцева
|
d |
0 |
30° |
45° |
50° |
60° |
|
A |
0 |
0,577 |
1 |
1,192 |
1,732 |
|
|
1 |
6,917 |
22,67 |
36,03 |
109,18 |
|
|
1 |
7 |
22,55 |
36 |
110 |
Приведем уравнение (8) к стандартной форме
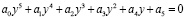 (10)
(10)
Запишем формулы для коэффициентов 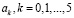
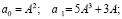
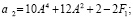
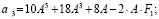 (11)
(11)
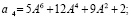
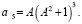
Таким образом, при A>0 коэффициенты 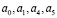 являются положительными, а коэффициенты
являются положительными, а коэффициенты 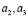 могут менять знак.
могут менять знак.
Представим коэффициенты 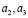 в форме
в форме
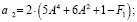
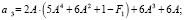 (12)
(12)
Из (12) нетрудно видеть, что
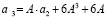 .
.
Рассмотрим таблицу возможных знаков в наборе коэффициентов 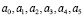 .
.
Таблица 2
|
№ п/п |
a0 |
a1 |
a2 |
a3 |
a4 |
a5 |
|
1 |
+ |
+ |
+ |
+ |
+ |
+ |
|
2 |
+ |
+ |
0 |
+ |
+ |
+ |
|
3 |
+ |
+ |
– |
+ |
+ |
+ |
|
4 |
+ |
+ |
– |
0 |
+ |
+ |
|
5 |
+ |
+ |
– |
– |
+ |
+ |
Проиллюстрируем применение табл. 2 на примере. Известно из номограммы Б.Т. Емцева, что при 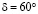 и
и 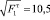 существует единственный корень
существует единственный корень 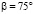 . Установим, к какому варианту относится этот случай. Найдем коэффициенты
. Установим, к какому варианту относится этот случай. Найдем коэффициенты 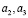 .
.
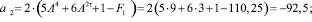
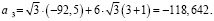
Этот случай соответствует пятому варианту табл. 2. Уравнение (10) в этом случае может иметь два положительных корня, может иметь один совпадающий положительный корень и может не иметь положительных корней.
Для нахождения положительных корней уравнения (8) была написана программа в среде Maple 9.5. Входными данными для определения корней являются значения 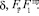 Выходной параметр – угол b.
Выходной параметр – угол b.
Для поиска положительных корней уравнения (8) определяем верхнюю границу этих корней [3]
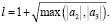 (13)
(13)
Таким образом, в заданном диапазоне [0;l] с помощью программы отыскиваются корни уравнения (8). Количество корней, и их значения определяются как графически, так и аналитически.
Результаты расчетов для широкого диапазона значений угла d приведены в табл. 3.
Таблица 3
Расчетные и табличные значения угла b
|
№ п/п |
d |
F1 |
|
bтабл |
bрасч |
|
1 |
30° |
16 |
0,46045 |
47° |
46,15° |
|
2 |
35° |
25 |
0,41464 |
48° |
48,13° |
|
3 |
45° |
49 |
0,47254 |
56° |
55,8° |
|
4 |
50° |
56,25 |
0,68387 |
62° |
61,94° |
|
5 |
60° |
111,5 |
1,98276 |
75° |
75,0° |
|
6 |
70° |
200 |
11,6865 |
– |
86,05° |
|
7 |
72° |
210 |
15,1456 |
– |
87,16° |
|
8 |
72° |
220 |
16,9245 |
– |
86,84° |
|
9 |
75° |
230 |
22,8348 |
– |
87,8° |
bтабл – значения угла направления косого гидравлического прыжка по номограмме Б.Т. Емцева; bрасч – расчетные значения угла направления косого прыжка.
Из табл. 3 нетрудно видеть, что значения bтабл и bрасч практически совпадают при 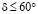 , однако предложенная программа позволяет рассчитывать значение b и при
, однако предложенная программа позволяет рассчитывать значение b и при 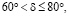 что важно для практики.
что важно для практики.
Далее, определив значение угла b, находим значение параметра h из (1), а затем и параметры потока после прыжка
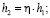
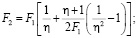
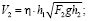 (14)
(14)
Определим значения гидродинамического напора до удара струи потока о боковую стенку русла и после удара:
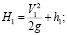
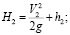 (15)
(15)
Определим относительные потери энергии при набегании струи потока на боковую стенку
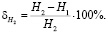
Результаты расчетов приводим в табл. 4.
Таблица 4
|
№ п/п |
F1 |
d |
h1, м |
b |
h2, м |
F2 |
H1, м |
H2, м |
dН, % |
|
1 |
16 |
30° |
0,2 |
46,2° |
0,722 |
2,304 |
1,80 |
1,553 |
13,68 |
|
2 |
25 |
35° |
0,14 |
48,1° |
0,67 |
2,456 |
1,89 |
1,93 |
21,01 |
|
3 |
49 |
45° |
0,092 |
55,8° |
0,709 |
2,083 |
2,346 |
1,447 |
38,33 |
|
4 |
56,25 |
50° |
0,081 |
61,9° |
0,718 |
1,47 |
2,359 |
1,246 |
47,17 |
|
5 |
111,5 |
60° |
0,059 |
75° |
0,822 |
0,57 |
3,348 |
1,058 |
68,4 |
|
6 |
200 |
70° |
0,041 |
86,1° |
0,798 |
0,075 |
4,141 |
0,828 |
80,01 |
|
7 |
210 |
72° |
0,04 |
87,2° |
0,799 |
0,052 |
4,24 |
0,82 |
80,66 |
|
8 |
220 |
72° |
0,039 |
86,8° |
0,798 |
0,058 |
4,33 |
0,821 |
81,04 |
|
9 |
230 |
75° |
0,038 |
87,8° |
0,796 |
0,041 |
4,408 |
0,812 |
81,58 |
Выводы
1. В работе предложен метод численного определения направления фронта косого гидравлического прыжка и потери напора для элементарных струй в точке набегания потока на боковую стенку.
2. Такой подход и является обоснованием выбора законов «масса – количество движения» для описания явления косого гидравлического прыжка.
3. Угол набегания крайней линии тока на боковую стенку в предложенной модели может изменяться в диапазоне 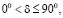 что соответствует эксперименту.
что соответствует эксперименту.