Старость и старение населения вышли в последние годы на уровень глобальных проблем человечества. Проблемность этих процессов связана с массой нерешенных социальных, экономических, культурных и медицинских задач по обеспечению и созданию оптимальных условий жизнедеятельности людей пожилого возраста.
Проблема старения общества представляет собой новый социальный феномен, с которым человечество столкнулось лишь во второй половине XX века. Сегодня российское общество вплотную подошло к такому периоду своего развития, когда увеличение доли пожилых людей в составе населения серьезно влияет на экономические, политические, социальные, духовно-нравственные изменения. Реализация идей построения "общества для людей всех возрастов" ставит в качестве важнейшей в российском обществе задачу формирования в общественном сознании положительного образа старости, уважения к пожилым людям, использование их потенциала в экономике.
Категория пожилых людей имеет сложную структуру, разбивается на большое количество страт, как пересекающихся между собой, так и не имеющих пересечения. При этом многим стратам присущи одинаковые функции, возможно, с различными значениями [1, 2]. Так как страты с течением времени могут изменяться, появляются новые или исчезают уже имеющиеся, то исходную решетку полезно представлять себе потенциально бесконечной, а само множество страт в виде иерархической системы. Дадим необходимые определения.
Упорядоченным множеством L называется множество, на котором определено бинарное отношение x≤y, удовлетворяющее для любых элементов x, y, z из L следующим условиям: 1. x≤x (рефлексивность), 2. если x≤y и y≤x, то x=y (антисимметричность), 3. если x≤y и y≤z, то x≤z (транзитивность). Далее, элемент, a упорядоченного множества L называется точной верхней (нижней) гранью элементов x и y этого множества, если x≤a, y≤a (a≤x, a≤y) и для любого b, такого, что x≤b, y≤b (b≤x, b≤y) имеет место, a≤b (b≤a). Точная верхняя грань элементов x, y обозначается x![]() y, а точная нижняя x
y, а точная нижняя x![]() y. Упорядоченное множество L, в котором для любых элементов этого множества определена точная верхняя и точная нижняя грань называется решеткой.
y. Упорядоченное множество L, в котором для любых элементов этого множества определена точная верхняя и точная нижняя грань называется решеткой.
Определение 1. Подмножество I решетки L называется иерархией, если для любых двух элементов множества I определена их точная верхняя грань.
Следующие два эквивалентных условия для элементов x, y, z решетки L называются дистрибутивностью:
- x
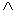 (y z) = (x
(y z) = (x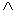 y)
y) 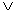 (x
(x 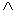 z)
z) - x
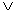 (y
(y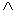 z)=(x
z)=(x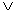 y)
y) 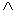 (x
(x 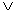 z), а условие
z), а условие - если x≤z, то x
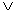 (y
(y 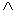 z)= (x
z)= (x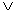 y)
y)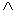 z - модулярностью.
z - модулярностью.
Если условия 1, 2 выполняются для любых элементов x, y, z решетки L, то эта решетка называется дистрибутивной, а если для любых элементов x, y, z выполняется условия 3., то решетка называется модулярной [3]. Любая дистрибутивная решетка модулярна, но обратное не верно. В иерархии существуют страты x, y, z, для которых не выполняется условия 1, 2 и 3.
Утверждение 1. Существует немодулярная решетка, содержащаяся в иерархии страт.
Доказательство. Обозначим через S0 - страту пожилых людей, являющихся либо УВОВ, либо инвалидами 1 группы, S1 - страту пожилых людей являющихся УВОВ, S2 - страту пожилых людей инвалиды 1 группы, S3 - страту пожилых людей ИВОВ, S4 - страту пожилых инвалидов 1 группы УВОВ. Тогда выполняются следующие равенства: S0 =S1 ![]() S2, S3 ≤ S1, S4 =S2
S2, S3 ≤ S1, S4 =S2 ![]() S3.
S3.
Докажем, что для элементов S1, S2, S3 не выполняется тождество модулярности. Действительно, S3≤S1, рассмотрим элемент S3![]() (S2
(S2 ![]() S1). Так как S2
S1). Так как S2 ![]() S1= S4, а S3
S1= S4, а S3 ![]() S4=S3, то S3
S4=S3, то S3 ![]() (S2
(S2 ![]() S1)=S3. С другой стороны, вычислим элемент (S3
S1)=S3. С другой стороны, вычислим элемент (S3 ![]() S2)
S2) ![]() S1, так как S3
S1, так как S3 ![]() S2= S0, а S0
S2= S0, а S0 ![]() S1= S1, то (S3
S1= S1, то (S3 ![]() S2)
S2) ![]() S1=S1. Таким образом, S3
S1=S1. Таким образом, S3 ![]() (S2
(S2 ![]() S1)≠(S3
S1)≠(S3 ![]() S2)
S2)![]() S1, более точно S3
S1, более точно S3 ![]() (S2
(S2 ![]() S1)< (S3
S1)< (S3 ![]() S2)
S2) ![]() S1, что и доказывает немодулярность построенной решетки.
S1, что и доказывает немодулярность построенной решетки.
Замечание. Отметим, что внеся даже небольшие изменения в построении примера из утверждения 1 можно получить модулярную решетку.
Пример 1. Пусть S0 - страта пожилых людей являющихся либо инвалидами, либо людьми имеющими высшее образование, S1 - пожилые люди инвалиды, S2 - пожилые люди с высшим образованием, S3 - пожилые люди инвалиды 1 группы, S4 - пожилые инвалиды с высшим образованием, S5 - пожилые инвалиды 1 группы с высшим образованием. Тогда S0=S1 ![]() S2, S3≤S1, S4=S1
S2, S3≤S1, S4=S1 ![]() S2, S5=S2
S2, S5=S2 ![]() S3. Рассмотрим элемент S3
S3. Рассмотрим элемент S3 ![]() (S2
(S2 ![]() S1), получим S3
S1), получим S3 ![]() S2= S0 и S0
S2= S0 и S0 ![]() S1= S1. Таким образом, S3
S1= S1. Таким образом, S3 ![]() (S2
(S2 ![]() S1)=(S3
S1)=(S3 ![]() S2)
S2) ![]() S1 модулярность, для элементов S1, S2, S3 выполняется.
S1 модулярность, для элементов S1, S2, S3 выполняется.
Можно отметить, что большинство подрешеток в иерархии страт все - таки удовлетворяют этому условию. Более того, в любой иерархии можно построить подрешетку удовлетворяющую условию не только модулярности но и дистрибутивности.
Утверждение 2. В любой иерархии существует последовательность страт Si1 , Si2 , ... Sin , которые образуют дистрибутивную подрешетку.
Часто является необходимым оценить, насколько две страты близки друг к другу. Для этого введем понятие расстояния между стратами. Дадим следующее определение.
Определение 2. Расстоянием d (A, B) между стратами называется число
d= 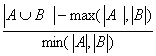 ,
,
где |A|, |B| - мощность страт A и B, min (a, b) - минимальное из чисел a, b, а max (a, b) - максимальное из чисел a, b.
Утверждение 3. Расстояния между стратами обладают следующими свойствами:
1. d (A, B)=1<=>A∩B=Ø
2. d (A, B)=0<=>A ⊂B или B ⊂A
3. 0≤d(A, B)≤1
В доказательстве следующего критерия немодулярности иерархии также используется понятие расстояния между стратами.
Утверждение 4. В иерархии I тогда и только тогда существует немодулярная подрешетка, когда в ней найдутся такие страты A, B, C, которые удовлетворяют следующим условиям:
1. d(A,C)=0, A≠C
2. d(A,B)>0
3. B∩C=A∩B (при этом если |B|<|А| это условие эквивалентно равенству d(A, B)=
d(B, C)).
Доказательства утверждений 2, 3, 4 будут рассмотрены в следующих работах.
СПИСОК ЛИТЕРАТУРЫ
- Клейменов В.Ф., Суровцева Н.Н., Функции для иерархии категорий пожилых людей // Фундаментальные исследования. № 10, 2008 г., С. 75.
- Клейменов В.Ф., Суровцева Н.Н., Вычисление для иерархии страт // Фундаментальные исследования. № 3, 2009 г., С.58-59.
- Биркгоф Г. Теория решеток. - М.: Наука.1984. - 568 с.



