Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Резюме
• Файлы

Зенкевич И.Г.

Закономерности изменения различных физико-химических констант органических соединений (А) в гомологических рядах идентичны и могут быть описаны простейшим линейным рекуррентным соотношением А(n+1) = aA(n) + b, связывающим их значения с величинами соответствующих констант для предыдущих гомологов.

Статья в формате PDF

149 KB

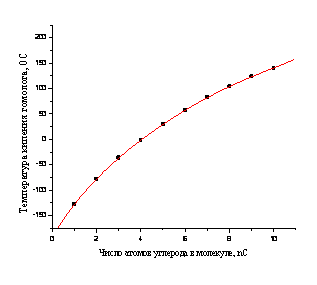
Среди многочисленных известных в настоящее время подходов к решению подобных задач, одна из групп методов основана на вы­явлении зависимостей, характеризующих изменения разных свойств (А) от положения соединений в соответ­ст­вующих гомоло­ги­ческих рядах, т.е. A = f(n_C), где n_C - число атомов углерода в мо­ле­­куле. Сложность такого подхода связана с их принципиально не­линейным характером. В качестве ил­люс­трации на Рис. 1а приве­ден график зависимости Т_кип(n_C) для перфтор-н-алканов C_nF_2n+2, а на Рис. 1б - динамических вязкостей h(n_C) для н-алканов. Такие зави­си­мос­ти могут быть как возрастающими (см. рисунок), так и убыва­ю­щи­ми (например, относительные плотности бромалканов), а также вы­пуклыми (см. рисунок), либо вогнутыми.

Аппроксимация подобных зависимостей полиномами разных фик­сированных степеней А = a₀ + a₁n_С + a₂n_С² + ... + a_kn_С^k (k = const) представляет собой пример формально-математического ре­шения задачи, которое обеспечивает приемлемую точность только в незначительных пределах вариаций числа атомов углерода в моле­кулах и не позволяет с приемлемой точностью вычислять экстрапо­ли­рованные значения неизвестных констант гомологов с большим числом атомов углерода по данным о простейших членах рядов.

Между тем, недавно выявлено общее соотношение, позволяю­щее при­ве­с­ти вариации лю­бых свойств органических соединений (А) в пре­делах гомологических рядов к линей­ному виду, что обес­печивает возможность их расчета для высших гомологов экстрапо­ляцией с высокой точностью. Оно связывает значения А любых чле­нов ряда со значениями этих же свойств для предыдущих гомо­логов, т.е. от­носится к рекуррентным уравнениям, ранее не приме­няв­шимся для решения подобных задач [1,2,5]:

A(n+1) = a A(n) + b          (1)

Значения a и b вычисляют методом наименьших квадратов; коэф­фициенты корреляции такой линейной зависимости для любых свойств органических соеди­не­ний (r) составляют не менее 0.999 (!).

Число примеров для иллюстрации возможностей применения этого универсального соотношения практически неограниченно (лю­бые свойства органических соединений любых гомологических рядов). Для графического представления выбраны всего два из них, которые можно сравнить с приведенными выше графиками нели­ней­ных зависимостей, а именно температуры кипения перфтор-н-алканов (Рис. 2а, ср. с Рис. 1а) и динамические вяз­кос­ти н-алканов (Рис. 2б, ср. с Рис. 1б). Параметры соответствующих корреляцион­ных рекуррентных уравнений приведены в подписи к рисунку.

Аналогичные рекуррентные зависимости соблюдаются для зна­че­ний показателей преломления, плотностей, поверхностных на­тя­же­ний, критических температур, критических давлений, энергий иониза­ции, диэлектрических проницае­мос­тей, дипольных момен­тов, коэф­фи­циентов распределения в гетерофазных системах и дру­гих свойств [2,5].

Уравнение (1) имеет следующее алгебра­и­ческое решение:

A(n) = k aⁿ + b (aⁿ - 1) / (a - 1)             (2)

где a, b, k - константы

Из такого решения следует несколько важных следствий. Во-пер­вых, уравнение (2) фактически представляет собой ряд, поскольку (aⁿ - 1) / (a - 1) = a^n-1 + a^n-2 + ... + a + 1. Однако интересно заметить, что степень (n) этого полинома не постоянна, а равна числу атомов углерода в молекуле гомолога (n_C), т.е. меняется в зависимости от положения соединения в ряду. Насколько известно автору, подоб­ные математические соотношения переменных степеней никогда ра­­нее не применяли для характеристики закономерностей вариаций физико-химических констант гомологов.

Во-вторых, при значениях коэффициентов a = 1, b ¹ 0 уравнения (1) и (2) трансформируются арифмети­ческие прогрессии A(n) = k + bn, а при a > 1 и b = 0 - в геометрические A(n) = kaⁿ. Следовательно, оба эти уравнения фактически объединяют два хорошо известных вида прогрессий в единую форму «арифметико-геометрических» прог­рес­сий. Именно этим объясняется возможность применения ре­кур­рентных соотношений для аппроксимации различных свойств ор­га­нических соединений.

В третьих, из того факта, что уравнения (1) и (2) описывают как арифметические, так и геометрические прогрессии, следует еще од­но уникальное свойство рекуррентных соотношений. Если они вы­полняются для значений различных свойств (А), то остаются спра­ведливыми и для логарифмов этих значений (lgA), а также для лю­бых степенных функций, в том числе экспоненциальных (e^A).

И, наконец, формула (2) как алгебраическое решение рекуррент­ного уравнения (1) впервые позволяет придать строгий математи­чес­кий смысл факту существования предельных значений некото­рых физико-химических свойств, который ранее был известен толь­ко на эмпирическом уровне. Из этой формулы следует, что при ги­по­тетическом увеличении числа атомов углерода в молекуле (n_C →∞) значения констант гомологов (А) могут как неограниченно воз­растать (при a > 1), так и стремиться к конечному пределу, а именно А(n_C →∞) = b / (a - 1) при a < 1. Некоторые из свойств каждого ти­па перечислены ниже.

Вне зависимости от отсутствия или существования предельных значений при n_C →∞ рекуррентные соотношения вида (1) примени­мы для описания любых свойств органических соединений.

Возможности использования не применявшихся ранее в хи­мии рекур­рентных соотношений пред­ста­в­ляются крайне разнооб­раз­ны­ми. Та­кой подход не только позво­ляет вычислять константы ранее не оха­рактеризованных органичес­ких соединений, но и (не ме­нее важ­но) легко проверять уже сущест­вую­щие справочные дан­ные с целью выявления среди них нена­деж­ных величин.

В качестве типичного примера обработки данных с использова­ни­ем рекуррентных соотношений можно рассмотреть проверку спра­­вочных данных по температурам кипения перфторкарбоновых кислот C_nF_2n+1CO₂H [4]. Для первых восьми членов ряда значения этих констант (⁰С) равны: 72.4 (CF₃CO₂H), 96.4 (C₂F₅), 120-122 (C₃F₇), 144.6 (C₄F₉), 162.7 (C₅F₁₁), 178.4 (C₆F₁₃), 190 (C₇F₁₅), и 202.4 (C₈F₁₇). Температура кипения перфтордекановой кислоты C₉F₁₉CO₂H в настоящее время неизвестна, а для перфторундека­но­вой кислоты C₁₀F₂₁CO₂H значение Т_кип (245 ⁰C) [4] в сравнении с дан­ными для предыдущих гомологов представляется аномально вы­соким. Сам факт приведения такой сомнительной величины в спра­воч­ном издании [4] свидетельствует о том, что приемлемые спосо­бы контроля надежности физико-химических констант органичес­ких соединений в настоящее время отсутствуют.

Однако для этих целей как нельзя лучше подходят рекуррент­ные соотношения вида (1). Температуры кипения всех гомологов С₂-С₉ перфторалкановых кислот подчиняются общему рекуррент­но­му соотношению T_b(n+1) = a T_b(n) + b, где a = 0.845 ± 0.011; b = 40.8 ± 1.8; r = 0.9996, S₀ = 0.9. Высокий коэффициент корреляции под­твер­ждает корректность всех значений Т_кип, а график этой зависи­мос­ти имеет столь же «идеальный» вид, как и графики, представ­лен­ные на Рис. 2. Да­лее, ис­пользуя пара­метры этой общей для сое­динений рассматриваемо­го клас­са зависи­мости, можно легко вычи­слить неизвестное ранее значе­ние темпе­ра­туры кипения перфтор­дека­новой кислоты:

T_кип(C₉F₁₉CO₂H) ≈ 0.845 ´ 202.4 + 40.8 ≈ 212 ⁰C

Применив это же соотношение дважды, получаем оценку темпе­ра­туры кипения перфторундекановой кислоты, которая оказывается на 25 ⁰С меньшей, чем справочное значение:

T_кип(C₁₀F₂₁CO₂H) ≈ 0.845 ´ 212 + 40.8 ≈ 220 ⁰C

Таким образом, известная величина Т_кип этого соединения (245 ⁰С) [4] яв­но ненадежна и требует пересмотра.

Использование рекуррентных соотношений позволяет изменить методологию уже, казалось бы, давно сложившихся алгоритмов вы­числений. Так, например, в хроматографии нередко возникает зада­ча предсказания параметров удерживания гомологов (что также мож­но рассматривать как одно из свойств органических соедине­ний) по данным о нескольких предыдущих членах тех же самых ря­дов. Теоретически метод решения таких задач считается давно из­вестным [3], посколь­ку существует общее соотношение, определя­ю­щее закономерности изменения времен удерживания (t_R) в зависи­мости от числа атомов уг­ле­рода в молекулах гомологов:

lg (t_R - t₀) = a n_C + b            (3)

где t₀ - так называемое «мертвое» время хроматографической систе­мы (время удерживания теоретически несорбирующегося компо­нен­та); коэффициенты a и b вычисляют методом наименьших квад­ратов.

Если значение t₀ предварительно не определено эксперимен­таль­но, то его можно оценить по временам удерживания трех по­сле­до­вательных гомологов (t_R1, t_R2 и t_R3) [3]:

t₀ ≈(t_R2² - t_R1 ´ t_R3) / (t_R1 + t_R3 - 2t_R2)      (4)

Оба соотношения (3) и (4) являются следствием известных фи­зи­ко-химических закономерностей хроматографических процессов, но, тем не менее, их применение не всегда позволяет решить задачу из-за слишком больших погрешностей результатов. В качестве при­ме­ра можно рассмотреть оценку времен удерживания н-алканов С₁₁-С₁₃ на ка­пил­лярной колонке с полидиметилсилоксановой фазой OV-101 при 110 ⁰С по данным о временах удерживания н-алканов С₅-С₁₀ (мин): 6.33 (пентан), 6.50 (гексан), 6.80 (гептан), 7.37 (октан), 8.41 (нонан) и 10.31 (декан). Используя приведенные в Табл. 1 пара­метры корре­ля­ционного уравнения (3) легко убедиться, что таким способом мож­но получить приемлемое значение t_R (с ошибкой -0.22 мин) толь­ко для «ближайшего» гомолога, элюируемого непосредст­венно после группы н-алканов С₅-С₁₀. Для следующих членов этого ряда ошибки достигают -0.78 мин (С₁₂) и -1.88 мин (С₁₃), что при ра­бо­те с капиллярными колонками практически бесполезно (в столь большие интервалы времен удерживания могут попадать сигналы нескольких десятков компонентов сложных смесей). В то же время рекуррентное соотношение (1) в виде t_R(n+1) = a t_R(n) + b позволяет получить намного более точные оценки времен удерживания не толь­ко ундекана, но и двух следующих за ним гомологов при су­ще­ст­венно более про­стых вычислениях (не требуются оценки вре­мен удерживания несорбирующегося компонента и логарифмиро­ва­ние значений t_R - t₀).

Таблица 1. Параметры корреляционного уравнения (3) и рекуррен­т­ного соот­но­шения (1) для оценки газохроматографических времен удержива­ния н-алканов

Таким образом, рекуррентные соотношения представляют собой класс функций, обладающих весьма интересными свойствами, что позволяет использовать их для аппроксимации самых разнообраз­ных зависимостей (несколько «необычных» примеров приведены в работе [5]). Что же касается различных свойств органических со­е­ди­­нений, то впер­вые установленный факт единого описа­ния зако­но­мернос­тей их изменения в гомологических рядах заслу­живает фор­мули­ров­ки в виде общего закона [2,5]: большинство из­вестных свойств ор­га­нических соединений линейно зависит от значений этих же свойств для предыдущих гомологов.

1а                                                                   1б

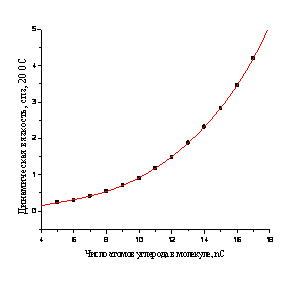
Рисунок 1. Графическая иллюстрация типичной нелинейной зависи­мос­­ти нормальных температур кипения (⁰С) гомологов от чис­ла атомов углерода (n_C) в молекуле (на примере пер­фтор-н-алканов C_nF_2n+2, 1 → n → 10 (а); аналогичная не­ли­ней­ная за­висимость динамической вяз­кос­ти (спз, 20 ⁰С)

от n_C на при­мере н-алканов С₅-С₁₆ (б).

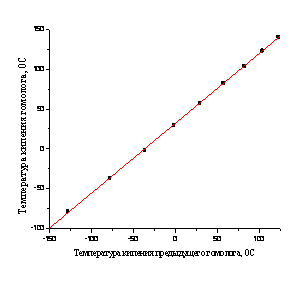
2а                                                                   2б

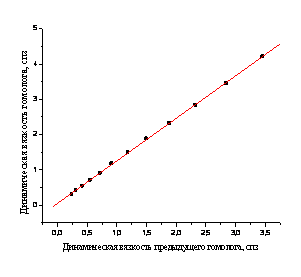
Рисунок 2. Линейная рекуррентная зависимость температур кипения Т_кип(n+1) = a Т_кип(n) + b для перфтор-н-­ал­ка­нов С₂-С₁₀: a = 0.876 ± 0.003, b = 32.0 ± 0.4, r = 0.9999, S₀ = 1.1 (a); анало­гич­ная линейная за­ви­си­мость для динамических вязкостей h(n+1) = a h(n) + b для н-алканов:

a = 1.204 ± 0.006, b = 0.053 ± 0.010, r = 0.9999, S₀ = 0.02 (б).

СПИСОК ЛИТЕРАТУРЫ

1. Зенкевич И.Г. Расчет температур кипения органичес­ких соеди­не­­ний по данным для пред­шест­­ву­ющих гомологов с использова­ни­­ем ре­­кур­рентных соотношений // Тез III научной сес­сии НИИ Химии СПб ун-та. СПб: 2004. С. 229-232.
2. Зенкевич И.Г. Общие закономерности изменения физи­ко-хими­чес­ких свойств органических со­единений в гомологических ря­дах //Журн. органич. химии. 2006. Т. 42. № 1. С. 9-20.
3. Leibnitz E., Struppe H.G. Hangbuch der Chromatographie. Leipzig, Academische Ver­lag, 1984.
4. Siegemund G., Feiring A., Smart R., Behr F., McKusick B. Fluorine compounds. Orga­nic. Ullmann´s Encyclopedia of Industrial Chemi­st­ry. 5^th Edn. V. A11. Verlagegesell­schaft mbH. Weinheim, Germany, 1988.
5. Zenkevich I.G. Simple Approximation of Any Constants of Homolo­gues Using Single Recurrent Functi­ons // Lecture Series on Com­pu­ter and Computatio­nal Sciences. 2005. V. 4B. P. 1574-1577.

Библиографическая ссылка