1. Вывод уравнений конвекции намагничивающихся смесей. Уравнения движения двух компонентных неэлектропроводных смесей в магнитном поле имеют вид [2,3]:
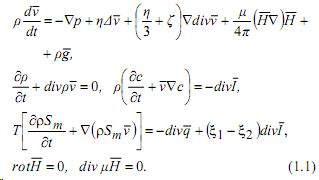
Здесь v¯ - скорость смеси, ρ - плотность смеси, c - концентрация первого компонента (c= ρ1/ ρ2) , Sm -энтропия единицы массы смеси, Т температура, ξ1 и ξ2 - химические потенциалы единицы массы для первого и второго компонентов соответственно, p давление смеси, η и ζ - коэффициенты вязкости смеси, q¯ вектор потока тепла, I¯ - вектор потока диффузии первого компонента, μ= μ (ρ,c,T,H¯) - магнитная проницаемость смеси, H¯ - магнитное поле, g¯ -ускорение свободного падения. Имея в виду вывод уравнений конвекции, вязкой диссипацией в уравнении притока тепла пренебрегаем [1]. Давление p в уравнении (1.1) записывается в виде:
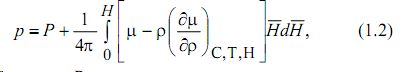
где P -давление в отсутствие магнитного поля при заданных значениях плотности, температуры и концентрации. Выражение для потоков:
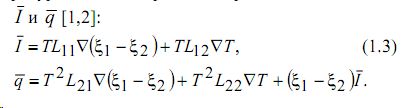
Здесь 
- кинетические коэффициенты, связанные между собой соотношениями взаимности Онзагера
Запишем тождество Гиббса для намагничивающихся смесей [2]:
Здесь G~m - потенциал Гиббса, приходящий ся на единицу массы среды, ξ=ξ1-ξ2; в качестве независимых термодинамических переменных в тождестве (1.4) выбраны c, p, T, H¯. Выражение для V¯ (с,p,T,H) имеет вид:
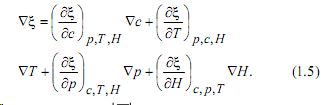
Здесь H = |H¯| ; среда предполагается изотропной.
Далее ограничимся случаем несжимаемой среды, уравнение неразрывности будем писать в виде div v¯= 0 . Из первой формулы (1.1) следует, что в состоянии равновесия выполняется условие:
Подставляя формулу (1.6) в (1.5) будем иметь:
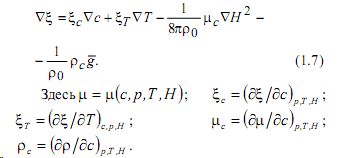
Аналогично (1.7) записывается уравнение для энтропии
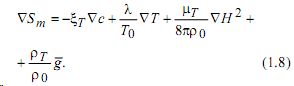
Здесь 
- удельная теплоемкость при постоянном давлении, концентрации и магнитном поле.
Будем считать, что отклонения величин от некоторых средних значений малы, поэтому в формулах (1.7) и (1.8) и далее коэффициенты при 
будем считать постоянными величинами, соответствующими некоторым средним значениям концентрации c0 , температуры T0 и магнитного поля 
Выражение для потоков I¯ и q¯ принимают вид:
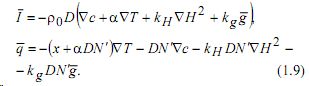
В формулах (1.9) вместо кинетических коэффициентов L11 , L12 , L22 введены другие параметры:
коэффициент диффузии:
коэффициент теплопроводности:
термодиффузионное отношение:
а также следующие параметры
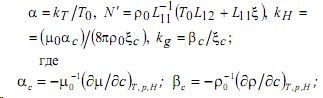
μ0 и ρ0 постоянные средние значения магнитной проницаемости и плотности. Все коэффициенты при градиентах в формулах (1.9) предполагаются постоянными.
Подставляя формулы (1.9) в третье и четвертое уравнение системы (1.1), будем иметь:
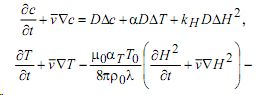
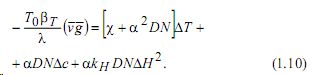
Здесь 
- коэффициент температуропроводности;
В уравнении притока тепла слагаемое, содержащее δH2 / δt , надо учитывать в случае переменного магнитного поля, например, в задачах, в которых в качестве модулируемого параметра берется магнитное поле.
Найдем теперь необходимые условия равновесия среды. Взяв rot от обеих частей уравнения (1.6), будет иметь вид:
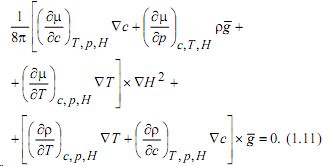
Из формулы (1.11) следует, что механическое равновесие в среде возможно в случае когда 
либо в
случае, когда векторы 
параллельны. Возможны и другие случаи равновесия когда эти векторы не обязательно вертикальны,но выбраны так, что выполняется условие (1.11). Далее ограничимся случаем, когда векторы вертикальны.
Линеаризуя уравнения (1.1) и (1.10) по малым конвективным возмущениям и предполагая, что 
имеем:
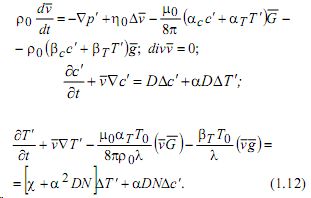
Здесь G¯=ΔH градиент магнитного поля, предполагаемый постоянной заданной величиной; c´ ,T´ - отклонения концентрации и температуры от постоянных средних значений c0 и T0 .
В случае G¯=const из уравнений (1.11), (1.12) следует, что необходимым условием равновесия является постоянство и вертикальность градиентов температуры и концентрации:
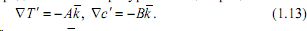
Здесь k¯ - единичный вектор, направленный вверх вдоль оси z.
Отметим, что вышеприведенные уравнения при отсутствии магнитного поля совпадают с уравнениями работы [1]
Магнитное поле в среде можно записать в виде H¯= H0¯ +H´¯, где H0¯ - поле при c0 = const , T0 = const , μ0= const ; H´¯ - возмущение. Так что G¯=G0¯ + G´¯ , где 
; величину G¯ можно считать заданной при выполнении условия G0 >>G´.
2. Уравнения конвективной диффузии. Интерес для приложений представляет случай когда температуру вдоль смеси можно считать постоянной. Конвективная диффузия несжимаемой смеси описывается первым уравнением системы (1.1) и первым уравнением (1.10), а также уравнением неразрывности div v¯ =0 и уравнениями магнитного поля. Для решения конкретных задач необходимо также задавать соответствующие граничные условия на поверхности полости с жидкостью. Вектор потока диффузии в случае T =const имеет вид:
Далее будем предполагать выполненным условие
и пренебрегать в формуле (2.1) слагаемым, связанным с полем тяжести.
Движение смеси при отклонении концентрации от постоянного среднего значения описываются уравнением:
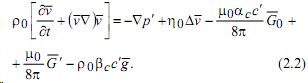
В уравнении (2.2) в отличие от уравнения (1.12) учитывается градиент магнитного поля G´¯, индуцированный неоднородностью концентрации. Вводя потенциал магнитного поля 
, из последних двух уравнений (1.1) имеем:
Здесь 
Полагая 
из формулы (2.3) находим:
Если геометрия задачи такова, что φ´ зависит только от z (z вдоль вектора k¯ ), из уравнения (2.4) следует:
Отсюда следует, что влияние градиента концентрации на магнитное поле надо учитывать в случае больших значений B.
Приведем к безразмерному виду стационарное уравнение конвективной диффузии:
Введем в рассмотрение Lc - характерное расстояние, на котором происходит существенное изменение концентрации, LH - характерное расстояние для градиента магнитного поля G, V0 - характерную скорость, G0 - характерный градиент магнитного поля. Обозначая безразмерные величины теми же буквами что и размерные, уравнение (2.5) можно записать в виде:
Здесь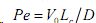 
- число Пекле, 
Если γ << 1 , влиянием магнитного поля на диффузию можно пренебречь. При выполнении условия Pe << 1 надо отбросить левую часть уравнения (2.6) и затем приравнять к нулю правую. Распределение концентрации в этом случае определяется уравнением:
Рассмотрим теперь задачу о конвективном движении смеси вблизи полубесконечной вертикальной пластины, на поверхности которой происходит гетерогенная изотермическая реакция. Предполагая скорость реакции бесконечно большой, запишем граничное условие для концентрации c = 0 на поверхности пластины (предполагается, что реагирует первая компонента).
Концентрацию вдали от пластины обозначим через c0. Будем считать, что заметное изменение концентрации происходит в тонком слое вблизи пластины, так что течение имеет вид пограничного слоя. Движение жидкости вдоль пластины происходит под действием поля тяжести и градиента магнитного поля. Пренебрегая индуцированным градиентом магнитного поля, запишем уравнения движения в приближении стационарного пограничного слоя [4]:
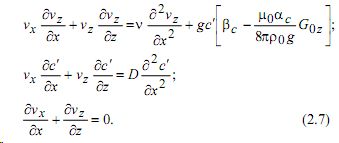
Здесь z - координата вверх вдоль пластины, x - перпендикулярно к пластине; нижней кромке пластины соответствует 
- компонента градиента поля.
Граничные условия:
В работе [4] показано, что система (2.7) может быть приведена к обыкновенным дифференциальным уравнениям. Распределение концентрации имеет вид:
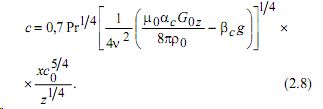
Здесь Pr = v/D - число Прандтля, предполагается что число Прандтля велико [4]. Из формул (2.1) и (2.8) следует, что плотность потока диффузии на пластину равна:
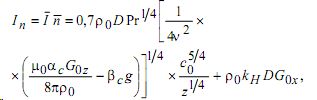
где G0x компонента градиента магнитного поля, n нормаль, направленная внутрь пластины. Таким образом, при помощи магнитного поля можно управлять диффузионными потоками на пластину, на поверхности которой происходит реакция.
Градиент приложенного магнитного поля предполагается достаточно большим по сравнению с индуцированным градиентом.
Литература
- Гершуни Г.З., Жуховицкий Е.М. Конвективная устойчивость несжимаемой жидкости М.: Наука, 1972. 392 с.
- Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Наука, 1982. 624 с.
- Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1988. 736 с.
- Левич В.Г. Физико-химическая гидродинамика. М.: ГИФМЛ, 1959. 700
Библиографическая ссылка
Тактаров Н.Г. КОНВЕКЦИЯ СМЕСЕЙ В МАГНИТНОМ ПОЛЕ // Успехи современного естествознания. – 2003. – № 7. – С. 13-16;URL: https://natural-sciences.ru/ru/article/view?id=14555 (дата обращения: 19.04.2024).