и 
. Соответственно определяются скорости и ускорения:
и 
. Если движение свободного тела происходит под действием силы F, то силу можно разложить на две составляющие 
. Работу, совершаемую силой, направленной вдоль перемещения, можно записать в виде 
. Используя соотношения: 
и 
, выражение для работы можно представить в следующем виде:
или 
(1)
где
- импульс силы. Для свободного тела импульс силы передается телу в виде импульса (количества движения) тела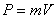 
, т.е. 
. Это выражение - II закон Ньютона. Поскольку работа (1) пропорциональна квадрату силы F, то для взаимно перпендикулярных сил 
и 
будет выполняться принцип аддитивности (независимости) работ: работу силы A можно представить в виде арифметической суммы работ
:
(2)
Однако, принцип аддитивности работ не применим к силам, действующим вдоль одной координатной оси. Пусть сила F представляет собой сумму двух сил:
. Запишем формально сумму работ этих сил. Не трудно убедиться на конкретных числовых значениях, что:
(3)
т.е. условие аддитивности не выполняется. На самом деле работа двух сил будет равна:
(4)
или
(4а)
В курсах физики для определения работы, затрачиваемой на разгон (или торможение) тела, используется теорема о кинетической энергии: изменение кинетической энергии материальной точки при её перемещении между двумя положениями равна работе, совершенной при этом силой: 
. Рассмотрим эту задачу, используя понятия импульса силы и количества движения.
Пусть свободное тело массы m движется равномерно и прямолинейно со скоростью 
. Требуется изменить его скорость, например, повысить до величины 
. Для этого необходимо сообщить телу дополнительный импульс 
(рис. 1а). Запишем закон сохранения импульса:
(5)
Формально запишем закон сохранения энергии (работ):
(6)
Однако нетрудно убедиться простым численным расчетом, что закон сохранения энергии в таком виде ошибочен вследствие неаддитивности работ.
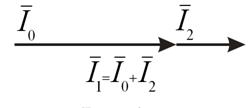
Рисунок 1а. Закон сохранения импульса
Поскольку вектора 
и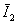 
лежат на одной прямой, то закон сохранения импульса (5) трактуют как алгебраическую сумму 
. Перепишем (5) из векторной формы в алгебраическую, используя теорему косинусов (рис. 1б):
(7)
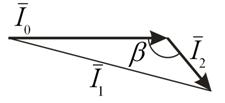
Рисунок 1б. Преобразование из векторной формы в алгебраическую закона сохранения импульса
Для нашего случая угол 
и 
. Тогда вместо (7) получим:
(8)
Разделив это выражение на удвоенную массу, получим закон сохранения энергии (работ):
(9)
Или в таком виде:
(9а)
Последний член:
где 
- квадрат среднегеометрической величины скорости, 2m - удвоенная масса при переходе из одной инерциальной системы ( ) к другой ( ).
Из уравнений (9) и (9а) найдем работу разгона (торможения):
(10)
А теперь рассмотрим случай, когда тело массы m под действием горизонтальной силы F начинает движение по шероховатой поверхности (коэффициент трения скольжения 
). Сила трения 
. Силу тяги можно представить в виде суммы: 
, где сила 
в соответствии со II законом Ньютона вызывает ускоренное движение тела:
. Во всех курсах физики работу силы тяги представляют в следующем виде:
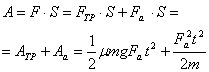(11)
Однако это выражение неверно, так как для сил, действующих вдоль одной оси, не выполняется принцип аддитивности работ. Запишем векторную сумму импульсов сил: 
, где , 
,
. Векторную сумму запишем в алгебраической форме (в общем случае надо использовать теорему косинусов):
Разделив все члены равенства на 2m, получим:
(12)
или
(12а)
где 
- суммарная работа силы тяги, 
- работа, затрачиваемая на увеличение кинетической энергии, 
- работа, затрачиваемая на преодоление силы трения при равномерном движении, 
- работа силы трения при ускоренном движении.
Автором в работах [1-3] была определена работа центростремительных и гироскопических сил. Определим её с помощью принципа аддитивности работ, совершаемых ортогональными силам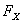и 
и 
(рис.2).
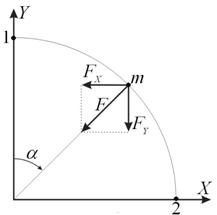
Рисунок 2. Принцип аддитивности работ, совершаемых ортогональными силам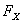и и
Пусть материальная точка m равномерно движется по окружности под действием центростремительной силы 
. Угол поворота 
, где 
или 
,T - период вращения. Силу F раскладываем на две составляющие:
и 
. Найдем импульсы этих сил:
;
;
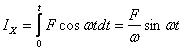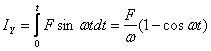Работа, совершаемая силой F, будет равна:
(13)
Т.е. получили то же самое выражение, что и в работах [1-3]. Для четверти окружности 
и работа 
, аналогично 
, 
.
СПИСОК ЛИТЕРАТУРЫ
- Иванов Е.М. Работа центростремительных и гироскопических сил //Вестник ДИТУД. - 2003. - №1.
- Иванов Е.М. Дополнительные главы классической механики. Димитровград, ДИТУД УлГТУ, 2004.
- Иванов Е.М. Работа центростремительных и гироскопических сил //Успехи современного естествознания. - №9. - 2004.
Библиографическая ссылка
Иванов Е.М. ОБ АДДИТИВНОСТИ РАБОТ В КЛАССИЧЕСКОЙ МЕХАНИКЕ // Успехи современного естествознания. – 2005. – № 12. – С. 10-12;URL: https://natural-sciences.ru/ru/article/view?id=9611 (дата обращения: 19.04.2024).