Рассматривается цилиндрический корпус аппарата, под воздействием циклической сосредоточенной нагрузки. Решение задачи строим на основе общей теории цилиндрических оболочек.
Выбираем в качестве основной неизвестной функции прогиб оболочки 
и исключаем перемещения 
и 
. В результате разрешающую систему дифференциальных уравнений сводим к одному дифференциальному уравнению восьмого порядка относительно неизвестной функции 
. Для решения этого уравнения применяем метод разложения неизвестной функции w и внешней нагрузки в двойные ряды Фурье:
, (1)
(2)
где K - число локальных радиальных нагрузок в заданном поперечном сечении цилиндрической оболочки, х, 
- цилиндрические координаты, L - длина оболочки.
Проведя ещё ряд преобразований, получаем следующие значения для коэффициентов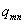 
:
= 
, (n = 1,2, ...), (3)
= 
, (m = 1,2, ...; n = 1,2, ...), (4)
где Р - сосредоточенная нагрузка; r - радиус оболочки.
Через коэффициенты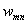 
и 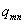определяются меридиональные и кольцевые усилия и изгибающие моменты, меридиональные и кольцевые напряжения, а так же осевые и окружные перемещения.
Реализация предложенного метода и алгоритма компьютерного численного анализа напряженно-деформированного состояния конструкции осуществлена в виде пакета прикладных программ. Программный продукт предназначен для применения в отраслевых САПР и ERP-системах, допускает автономное использование.
Библиографическая ссылка
Аноприенко Р.В. КОМПЬЮТЕРНЫЙ АНАЛИЗ НЕСУЩЕЙ СПОСОБНОСТИ ТОНКОСТЕННЫХ ЭЛЕМЕНТОВ КОНСТРУКЦИИ ПОД ДЕЙСТВИЕМ ЦИКЛИЧЕСКОЙ СОСРЕДОТОЧЕННОЙ НАГРУЗКИ // Успехи современного естествознания. 2006. № 10. С. 45-46;URL: https://natural-sciences.ru/ru/article/view?id=11610 (дата обращения: 17.12.2025).