Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Файлы

Романовский Р.К. Воробьева Е.В. Макарова И.Д.

Статья в формате PDF

121 KB

В работах [1-4] изучалось асимптотическое поведение решений задачи Коши для линейных гиперболических систем с одной пространственной переменной - устойчивость, дихотомия, экспоненциальная расщепляемость - на основе построенного в [1,5] аппарата матриц Римана первого и второго рода, представляющих собой соответственно сингулярную и регулярную компоненты фундаментальной матрицы гиперболической системы. В [6] предложен подход к анализу устойчивости решений задачи Коши, основанный на приведении гиперболической системы к обыкновенному дифференциальному уравнению с ограниченным операторным коэффициентом в гильбертовом пространстве и последующем применении метода функционалов Ляпунова. В данной работе рассматривается смешанная задача для почти линейной гиперболической системы с одной пространственной переменной, встречающаяся в задачах акустики, теории упругости, химической кинетики [7-11]. Ранее в работе [10] исследовалась устойчивость стационарных решений этой задачи первым методом Ляпунова, установлен спектральный признак экспоненциальной устойчивости в  норме. Ниже предложен вариант метода функционалов Ляпунова для этой задачи, установлен признак экспоненциальной устойчивости в  норме в терминах матричных неравенств.

Рассматривается краевая задача для гиперболической системы с кратными характеристиками

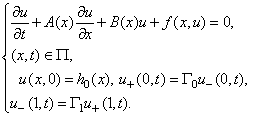       (1)

Здесь П-полуполоса

; 

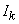   - единичная матрица порядка ,   - строка размера N_k;  - постоянные матрицы соответствующих размеров. Матрицы A, B и векторы  - гладкие в своих областях определения,  равномерно по  при . Здесь и далее  - евклидова норма в , знак * означает транспонирование. Предполагаются выполненными условия согласования нулевого и первого порядков:

  (2)

где  При указанных условиях имеет место локальная однозначная разрешимость краевой задачи (1) в классе гладких функций [7]. Далее будем дополнительно предполагать: существует такое r > 0 что при условии  имеет место однозначная гладкая разрешимость во всей полуполосе . Можно считать . В силу оценки (2) начальной функции отвечает решение .

Обозначим через H множество гладких функций , удовлетворяющих условиям (2) с заменой h_k на h, 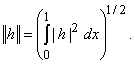Значения решения  краевой задачи (1) при каждом t - элементы H. Будем говорить, что решение  задачи (1) экспоненциально устойчиво в L₂-норме, если существуют такие числа  что для решений задачи (1), удовлетворяющих условию , верна оценка

Зафиксируем гладкую [0,1] на  матрицу  где блоки G_k имеют такие же размеры, как соответствующие блоки матрицы A, и удовлетворяют условиям

Представим матрицы A,G  в виде  где  имеют порядок  и построим матрицы

ТЕОРЕМА. Для экспоненциальной устойчивости в L₂-норме решения u=0 краевой задачи (1) достаточно существование матрицы G с указанными свойствами такой, что выполняются неравенства

ЛИТЕРАТУРА

1. РомановскийР.К. О матрицах Римана первого и второго рода //Докл. АН СССР. 1982. Т.267,№ 3. C.577-580.
2. РомановскийР.К. Экспоненциально расщепляемые гиперболические системы с двумя независимыми переменными // Мат. сб. 1987. Т.133, № 3. С.341-355.
3. РомановскийР.К. Об операторе монодромии гиперболической системы с периодическими коэффициентами // Применение методов функционального анализа в задачах математической физики. Киев: ИМ АН УССР, 1987. С.47-52.
4. РомановскийР.К. Усреднение гиперболических уравнений//Докл. АН СССР. 1989. Т.306, № 2. C.286-289.
5. РомановскийР.К. О матрицах Римана первого и второго рода //Мат. сб. 1985. Т.127, № 4. С.494-501.
6. ВоробьеваЕ.В., РомановскийР.К. Об устойчивости решений задачи Коши для гиперболической системы с двумя независимыми переменными // Сиб. мат. журн. 1998. Т.39, № 6. С.1290-1292.
7. АболиняВ.Э., МышкисА.Д. Смешанная задача для почти линейной гиперболи-ческой системы на плоскости //Мат. сб. 1960. Т.50, №4. С.423-442.
8. ЗеленякТ.И. О стационарных решениях смешанных задач, возникающих при изучении некоторых химических процессов //Дифференц. уравнения. 1966. Т.2, №2. С.205-213.
9. ГодуновС.К. Уравнения математической физики //М.: Наука. 1979.
10. ЕлтышеваН.А. О качественных свойствах решений некоторых гиперболи-ческих систем на плоскости // Мат. сб. 1988. Т.135, №2. С.186-209.
11. АкрамовТ.А.Качественный и численный анализ модели реактора с противотоком компонентов // Математическое моделирование каталитических реакторов. Новосибирск: Наука, 1989. С.195-214.

Библиографическая ссылка