Введение
Сегодня все больше внимания уделяется разработке новых эффективных технологий обогащения трудноизвлекаемых полезных ископаемых. Для объектов добычи золота характерно вовлечение в отработку месторождения с более низким содержанием золота и трудноизвлекаемым фракциями, как мелкого и тонкого золота, что диктует необходимость усовершенствования существующих методов и способов обогащения. Наиболее это характерно для широко используемых гравитационных методов обогащения [1–3], которые, как известно, являются менее затратными из всех существующих и экологически безопасными.
При обогащении россыпей, содержащих мелкие, тонкие классы золота, такая проблема, как извлечение полезного компонента, решается путем использования новых разработок отечественного и зарубежного производства в различных конструкциях и типах обогатительного оборудования [4–6].
Одним из них, в части реализации инновационных предложений, является крутонаклонный концентратор конструкции ИГДС СО РАН, разрабатываемый в лаборатории обогащения полезных ископаемых. Конструкция концентратора постоянно усовершенствуется, но главным является принцип его работы, который выражается в комплексном использовании разделительных процессов минеральных частиц по плотности и по крупности в объеме восходящего потока воды на тонком приповерхностном ее слое (на осадительной поверхности концентратора) [7].
В ходе разработки концентратора были спроектированы и изготовлены разные лабораторные образцы концентратора, написаны методики проведения исследований и проведены экспериментальные работы.
Основной процесс классификации происходит в рабочей зоне по принципу равнопадаемости или гидравлической классификации, а на осадительной поверхности пластин, учитывая метод поведения частиц на наклонной плоскости, под действием силы гравитации. В результате использования двух видов разделения в аппарате, одновременно происходит классификация минерального сырья по гидравлической равнопадаемости и разделение по гидравлической крупности или плотности.
Цель исследования – моделирование процессов разделения минеральных смесей на осадительной поверхности концентратора для оценки влияния режимных (формирование технологических потоков) и конструктивных параметров.
Материалы и методы исследования
Сложность процесса разделения минеральных зерен в рабочей зоне как многофакторного процесса требует применения современных методов, в том числе физико-математической модели процесса разделения минеральных смесей на осадительной поверхности концентратора. Научная новизна работы заключается в разработке физико-математической модели движения частиц в рабочей камере разработанного крутонаклонного концентратора и алгоритма определения вероятности извлечения тяжелых частиц в концентратор с использованием статистического метода.
Объектом моделирования является крутонаклонный концентратор, принципиальная схематическая конструкция которого представлена на рис. 1, состоящий из корпуса (1), загрузочного узла (2), отверстия для ввода транспортной воды (3), патрубка подачи воды для создания среды разделения (4), наклонной нарифленной поверхности (5), камеры для сбора концентрата (6), канала для удаления хвостов (7).
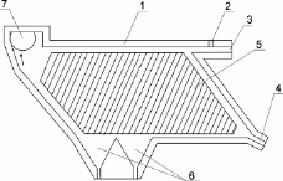
Рис. 1. Схема концентратора
Минеральное сырье подается через загрузочное отверстие в виде пульпы в концентратор. В верхней части рабочей камеры частицы распределятся по рифлям, где происходит гравитационная дифференциация в вееровидном движении частиц в зависимости от угла наклона концентратора. В зоне разделения легкие частицы увлекаются потоками воды и выводятся из рабочей камеры разгрузочным каналом, а тяжелые под действием гравитации спускаются вниз между рифлями и разгружаются в камеру сбора концентрата.
В основу физической модели заложен процесс разделения минералов, начиная с начальной стадии ввода минеральных зерен с дифференциацией их распределения по верхней части концентратора (надрифленной части концентратора) в зависимости от крупности и плотности частиц (рис. 1). Через патрубок для подачи исходного материала 6 загружается однородный поток зерен с различной плотностью. Зерна движутся под действием силы потока воды, поступающей в концентратор через патрубок 7, и силы тяжести (рис. 2). Также на них действуют силы реакции рабочей поверхности концентратора и трения.
Зерна тяжелой фракции, попадая в межрифленное пространство, не могут покинуть его вследствие действия поперечно направленного потока воды и перемещаться по наклонной плоскости, в отличие от частиц менее плотных, которые по мере нисходящего движения по наклонной плоскости будут увлекаться потоком, то есть происходит последовательная перечистка тяжелой фракции.
Согласно физико-математической модели движения частицы в концентраторе, зная физические свойства частицы (массу, форму, размер), параметры устройства (угол наклона рабочей поверхности, скорость потока воды) и параметры движения (начальные положения частицы, коэффициент силы трения), можно определить закономерности движения зерен. Это позволяет расчитывать возможные положения частицы в устройстве и разработать алгоритм определения распределения вероятности по рифлям, что дает возможность рассчитать показатели разделения минеральных частиц в концентраторе.
Диапазон угла наклона нарифленной поверхности находится в пределах 60–80º от горизонта.
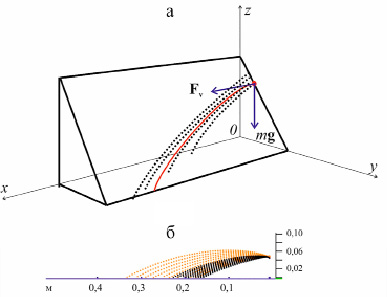
Рис. 2. Траектории движения частиц в верхней (загрузочной) части концентратора (а) и результат моделирования (б) по пескам (светлые точки) и по магнетиту (темные точки)
Уравнение движения для одной частицы с учетом силы реакции поверхности под действием однородного потока воды с определенной скоростью vv, направленного горизонтально, имеет вид
,
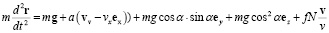где m – масса частицы, a – коэффициент силы потока воды, зависит от формы и массы частицы, vv – скорость потока воды, f – коэффициент трения о поверхность.
Разлагая по компонентам, получаем систему уравнений:
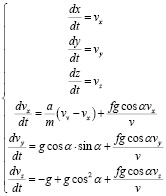
Система решается методом Рунге-Кутты.
Решение этой системы для частиц песка и магнетита (масса частицы песка равна 1 мг, частицы магнетита – 1,6 мг), которые далее будут участвовать в экспериментальной части работы, приводит к траектории (рис. 2, б) движения частиц песка и магнетита при скорости воды 2 м/с, рассчитанных по этому методу. Согласно методу, предложенному в работах [8, 9], вероятность положения частицы вдоль горизонтальной оси на уровне 0 прямо пропорциональна количеству частиц, проходящих через этот уровень за единицу времени. С этого уровня определяется количество частиц (в процентах), которые окажутся в определенных ячейках (межрифленное пространство), данного размера. При этом принято, что начальное произвольное направление скорости частиц соответствует изотропному распределению направлений начальных скоростей возможных частиц.
Частицы, попадая в верхнюю часть межрифленного пространства, движутся под действием силы тяжести и потока воды. Из-за геометрии устройства в нем частица пытается занять место в углу между рифлями и плоскостью. В этой области согласно модели происходит вихревое движение жидкости (рис. 3). Поэтому для расчета распределения частиц по массам внутри этой области, необходимо определение скорости частицы в момент входа частицы в область вихревого движения жидкости.
При ламинарном течении жидкости над рифлями в области между рифлями образуется вихревое движение жидкости (рис. 3). Образование вихревого движения можно объяснить следующим образом: на границе ламинарного и вихревого движения жидкость рассматривается как вязкая, и крайняя часть вихревого движения жидкости увлекается ламинарным течением.
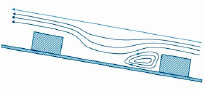
Рис. 3. Вихревое движение жидкости в области между двумя рифлями
В работе [10, с. 195] рассматривается вихревое движение жидкости в траншее, наверху которой имеется ламинарное течение жидкости. Экспериментальные и теоретические исследования показали, что в этом случае соответствует вихревое движение жидкости с постоянной завихренностью. В рассматриваемой задаче завихренность постоянная ω и направлена перпендикулярно к плоскости (рис. 3), она связана со скоростью жидкости v соотношением: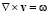 
. В первом приближении при моделировании вихревого движения частицы принимается, что жидкость в этой области устройства вращается по круговой траектории. В этом случае система имеет аксиальную и цилиндрическую симметрию, то есть задача является плоской. Несложные вычисления показывают, что при данных условиях, интегрирование уравнения 
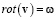дает линейное распределение скорости вдоль радиуса цилиндра. На периферии жидкость вращается со скоростью прилегающей к ней ламинарного течения, в центре этой области скорость жидкости равна нулю. Из-за геометрии устройства тяжелые зерна породы в желобе попадают в зону вихревого движения жидкости. Более тяжелые частицы занимают место около оси вращательного движения жидкости. Совершая вращательные движения под действием потока воды, зерна под действием силы тяжести (так как рабочая поверхность наклонена под углом 70⁰) сползают вниз. Траектория частиц имеет форму спирали. Периферийная часть области вихревого движения уносится потоком воды, подающейся через патрубок (3) из нижней части концентратора (рис. 1).
На рис. 4 приведен алгоритм расчета, где подпрограмма rkfixed решает систему дифференциальных уравнений методом Рунге – Кутты для многих частиц. При расчетах учитывалось то, что в уравнениях коэффициент силы потока воды и масса частицы входят как множитель a / m к скорости воды. Коэффициент a, согласно формуле Стокса, зависит от размера частицы линейно ~r, а масса пропорциональна объему частицы ~r3. Поэтому этот множитель пропорционален ~r–2. Расчеты проведены для частиц с размерами 3,5; 2,5; 1,5 мм.
По разработанному алгоритму вычисляется конечная вероятность нахождения частицы в определенной области рабочей поверхности устройства. Зная эту вероятность, можно определить количество частиц, пересекающих за некоторый промежуток времени горизонтальный уровень, граничащий с верхним краем рифлей. Таким образом, определяется распределение частиц на нарифленной части, а далее попадание их в камеры (2 камеры) накопителя тяжелых минералов в нижней части концентратора, что является равносильным показателю извлечения тяжелых минералов в моделируемом объекте.
Рис. 4. Алгоритм расчета для частиц магнетита с различной крупностью
Усредненные результаты экспериментальных исследований при различных крупностях частиц магнетита
|
№ |
Продукт |
Общий вес, г |
Песок, г |
Выход γ, % |
Магнетит, г |
Извлечение, % |
||
|
Наклон концентратора 60º поток 0,35 л/с, песок 200 г; магнетит класс +0,315 мм 10 г |
||||||||
|
1 |
Камера 1 |
15,98 |
9,68 |
7,64 |
6,3 |
63,00 |
||
|
Камера 2 |
46 |
42,33 |
21,99 |
3,67 |
36,70 |
|||
|
Хвосты |
147,23 |
147,2 |
70,37 |
0,03 |
0,30 |
|||
|
Всего |
209,21 |
199,21 |
100,00 |
10 |
100,00 |
|||
|
Наклон концентратора 60º поток 0,35 л/с, песок 200 г; магнетит класс -0,315+0,2 мм 10 г |
||||||||
|
2 |
Камера 1 |
13,39 |
10,74 |
6,42 |
2,65 |
26,24 |
||
|
Камера 2 |
46,13 |
40,3 |
22,11 |
5,83 |
57,72 |
|||
|
Хвосты |
149,11 |
147,49 |
71,47 |
1,62 |
16,04 |
|||
|
Всего |
208,63 |
198,53 |
100,00 |
10,1 |
100,00 |
|||
|
Наклон концентратора 60º поток 0,35 л/с, песок 200 г; магнетит класс -0,2 мм 10 г |
||||||||
|
3 |
Камера 1 |
6,76 |
6,04 |
3,25 |
0,72 |
7,19 |
||
|
Камера 2 |
49,25 |
44,75 |
23,68 |
4,5 |
44,91 |
|||
|
Хвосты |
151,94 |
147,14 |
73,07 |
4,8 |
47,90 |
|||
|
Всего |
207,95 |
197,93 |
100,00 |
10,02 |
100,00 |
|||
Результаты исследования и их обсуждение
Для сравнения полученных результатов с практикой разделения были проведены экспериментальные исследования извлечения тяжелых минералов. В таблице приводятся усредненные результаты экспериментальных исследований для частиц магнетита с различными крупностями.
При проведении экспериментов использовалась искусственная смесь, состоящая из 200 г речного песка и 10 г магнетита. Магнетит в качестве имитатора тяжелых минералов был выбран для удобства обработки полученных продуктов с помощью магнитной сепарации. Эксперименты проводились для частиц магнетита с различной крупностью: +0,315 мм, -0,315+0,2 мм, -0,2 мм; скорость подачи воды определялась расходометром и составляла от 0,35 до 0,42 л/с.
На рис. 5 приведены сравнения, полученные в ходе эксперимента данных с результатами теоретического расчета (по модели). По горизонтальной оси х точками 1, 2, 3 отмечены соответственно в 1 камере, во 2 камере и в хвостах, на вертикальной оси даны количества частиц песка (слева), магнетита (справа) в процентах (синий треугольник – экспериментальные данные, красный кружочек – теоретические).
Как видно из рис. 5, формы кривых (красные и синие линии) с некоторой небольшой погрешностью совпадают. График слева показывает выход песка. Как и ожидалось, в первой камере (точка 1 на горизонтальной оси) остается меньше песка, чуть больше во второй камере (точка 2), и основная часть песка уходит в хвосты (точка 3). График справа показывает извлекаемость магнетита в зависимости от крупности: а) +0,315 мм (в расчетах 0,35 мм), б) -0,315+0,2 мм (в расчетах 0,25 мм), в) -0,2 мм (в расчетах 0,15 мм). Тяжелые фракции крупностью +0,315 мм в основном остаются в первой камере (рис. 5, а), небольшая часть попадает во вторую камеру. Средние фракции крупностью -0,315+0,2 мм в основном падают во вторую камеру (рис. 5, б). Мелкие фракции крупностью -0,2 мм в основном уходят в хвосты (рис. 5, в). Таким образом, теоретическая модель достаточно хорошо описывает результаты натурного эксперимента.
Рис. 5. Сравнение экспериментальных данных с теоретическими результатами моделирования для частиц с различными крупностями: а) +0,315 мм, б) -0,315+0,2 мм, в) -0,2 мм
Заключение
Процесс разделения частиц на крутонаклонном концентраторе как мультифакторного процесса требует применения современных методов исследования.
Разработанная физико-математическая модель процесса разделения с учетом первоначального распределения частиц по разделительной поверхности и влияния образующихся вихревых движений частиц в межрифельном пространстве на основе метода ансамблей Гиббса и принципа суперпозиции систем позволяет получить близкие к экспериментальным расчетные значения.
Решение вероятностной задачи распределения частиц на надрифленной части и попадание их в камеры накопителя тяжелых минералов в нижней части концентратора равносильно показателю извлечения тяжелых минералов и хорошо коррелируется с результатами экспериментальных исследований в лабораторной модели концентратора по разделению частиц магнетита с различной крупностью (+0,315 мм, -0,315+0,2 мм, -0,2 мм) от песка.
Разработанная физико-математическая модель и алгоритм движения частиц в рабочей зоне концентратора позволит рассчитать извлечение тяжелых минералов, в зависимости от их класса крупности, в новой конструкции крутонаклонного концентратора.
Библиографическая ссылка
Матвеев А.И., Яковлев Б.В., Еремеева Н.Г., Нечаев П.Б. МОДЕЛИРОВАНИЕ ПРОЦЕССА ГРАВИТАЦИОННОГО РАЗДЕЛЕНИЯ МИНЕРАЛЬНЫХ ЧАСТИЦ В РАБОЧЕЙ ЗОНЕ КРУТОНАКЛОННОГО КОНЦЕНТРАТОРА // Успехи современного естествознания. – 2024. – № 12. – С. 99-106;URL: https://natural-sciences.ru/ru/article/view?id=38355 (дата обращения: 21.01.2025).