dQ = ÑТdS, или dS = dQ/ÑT. (1)
Этим определяется методологическое значение его применения в бетоноведении. Кроме того, скорость роста энтропии может сама по себе рассматриваться как важнейшая характеристика для прогнозирования процессов в физической системе. На основе этой характеристики можно анализировать стационарные состояния систем и изменение их свойств.
Согласно второму закону термодинамики, у всякой неизолированной бетонной системы энтропия состоит из двух слагаемых:
dS = dtS + deS, (2)
обусловленных изменением энтропии за счет внутренних dtS и внешних deS взаимодействий, причем dtS всегда ³ 0, тогда как 0 ³ deS ³ 0. Поэтому возрастание или убывание энтропии бетонной системы определяется в конечном итоге соотношением слагаемых в (2).
Если зафиксировать положение внешних тел, окружающих систему, то с течением времени любая физическая система придет в такое положение, когда её внутреннее состояние будет определяться только внешними параметрами и, не будет зависеть от начальных значений внутренних параметров. Это положение называется положением термодинамического равновесия, а время его установления - временем релаксации. В положении термодинамического равновесия все внутренние параметры системы одинаковы для всей системы, т.е. не зависят от координат и времени. С этой точки зрения процесс установления термодинамического равновесия можно рассматривать как процесс выравнивания внутренних параметров, который сопровождается соответствующими процессами переноса. Простейшим видом описания подобной связи является известный закон теплопроводности Фурье, устанавливающий зависимость между потоком теплоты и градиентом температур:
q = - l ÑT, (3)
где - q - удельный тепловой поток; l -коэффициент теплопроводности.
Термодинамическая идентичность l и S в уравнениях (1 и 3) позволяют провести анализ теплопроводности бетона по аналогии с уравнением (2). Следуя этой аналогии теплопроводность бетона в эксплуатационных условиях может быть выражена:
l(t) = l0 - Dl0(t) (4)
где l0 - теплопроводность бетона при завершении, в основном, процессов структурообразования; Dl0 - приращение, которое возникает в результате эксплуатационных воздействий за время t. Знак «минус» указывает, что релаксация теплопроводности связана с уравновешиванием конструктивных и деструктивных процессов, происходящих в бетоне, которые в целом приводят к уменьшению внутреннего напряжения и развитию необратимых деформаций.
В термодинамическом аспекте можно предположить, что скорость изменения теплопроводности пропорциональна её отклонению от равновесного значения (l^). В этом случае:
d(l-l^)/dt = -(l-l^)/t , (5)
где t - время релаксации.
Интегрируя и преобразуя, получаем:
l(t)=l0 - Dl0 е -(t)/t, (6)
Уравнение (6) можно считать общим уравнением теплопроводности бетона. Графическая интерпретация этого уравнения представлена на рис. 1.
Решение уравнения (6) сводится к минимизации l0 и t. Очевидно, что l0 представляет собой структурно - технологический, внутренний, аспект теплопроводности и должно прогнозироваться на стадии проектирования состава бетона. Время релаксации t зависит не только от природы внутреннего параметра l0, но и от характера нарушения его равновесного значения, в первую очередь за счет деструкции.
Учитывая, что теплопроводность бетона связана с энергетическим состоянием его структуры ΔU и энтропией ΔS, можно предположить, что постоянная времени релаксации определяется соотношением (DU/DS). Анализируя (DU/DS) в рамках основных уравнений термодинамики для процесса деформирования тел, получаем выражение:
DU/DS = Т + Θ grad T (7)
где Θ - объемные относительные деформации; Т- температура.
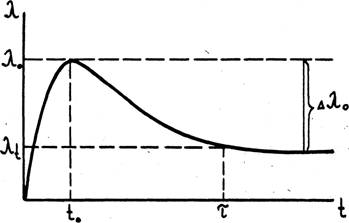
Рисунок 1. Графическая интерпретация общего уравнения теплопроводности бетона
Следовательно, релаксация теплопроводности, пропорциональна температуре эксплуатации и затуханию объёмных деформаций бетона, вызванных уровнем напряжения.
Экспериментальные исследования теплопроводности бетона (рис.2,3) подтвердили затухающий характер изменения Dl0 как функции времени и деформативности. Анализ этих результатов позволил получить уравнение изменения теплопроводности бетона во времени при фиксированном уровне напряжения:
l(t,h) =l0{1+Аt(Вt-1)+mh(1+0,93h) (1 -2 m)[1-mh(1+0,93h)(1-2m)]} (8)
где m - коэффициент Пуассона; h - уровни напряжения; t - время; А,В, - эмпирические коэффициенты, отражающие вид и качественные характеристики бетона.
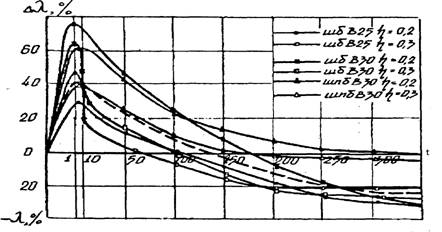
Рисунок 2. Изменение относительных приращений теплопроводности шлакобетонов во времени.
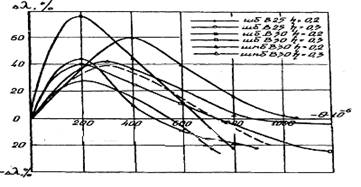
Рисунок 3. Влияние объёмных деформаций на приращения теплопроводности шлакобетонов.
С позиции термокинетической теории деформирования бетона и баланса энтропии, процесс релаксации теплопроводности также связан с увеличением энтропии.
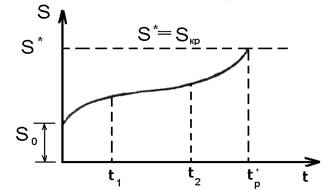
Рисунок 4. Схема роста энтропии бетона во времени при его деформировании
(S* - энтропийный критерий разрушения, t1 и t2 - границы инкубационной стадии).
Однако, в случае эксплуатации ограждающих конструкций из легкого бетона, кинетика этого процесса в основном заканчивается на «инкубационной» стадии (рис.4), когда в деформируемом бетоне зарождаются и накапливаются различного рода дефекты и повреждения. Этот процесс носит статистический характер и в каждый момент времени деформирования, заданным условиям напряжения, соответствует определенная степень повреждаемости структуры данного бетона. Приращение энтропии за счет внешнего взаимодействия затухает и в целом оно не достигает уровня «энтропийного критерия разрушения», что соответствует нижнему уровню границ микротрещинообразования легкого бетона.



