В данной статье авторы ограничились изучением и привлечением экспериментального материала, полученного другими исследователями, для анализа математических формулировок состояния локального термодинамического равновесия растворов при фазовых переходах в многолетнемерзлых горных породах.
Так, в работе [1] в качестве условия локального термодинамического равновесия для двухфазной зоны, определяющее взаимосвязь между температурой Т и концентрацией раствора С, рассматривается выражение следующего вида:
T=T0 - η (C - C0) (1)
В качестве определяющей гипотезы, теоретически допускающей ее применение, авторы предполагали, что эвтектика раствора может не достигаться, а должна обеспечиваться выбором соответствующих граничных условий [1]. В инженерной практике применение соотношения (1) давно апробировано и применяется для нейтральных растворов, а в случае применения для электролитов необходимо вводить поправочные коэффициенты. Например, часто рекомендуется применять формулу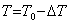 
для расчета температуры замерзания раствора. Причем для оценки ΔT считается достаточной применить выражение типа ΔT=Kf •m . Здесь Кf - коэффициент, имеющий смысл криоскопической постоянной растворителя, понимается понижение температуры замерзания раствора при растворении 1 гмоль вещества на 1 кг растворителя; m - моляльность растворенного вещества (число молей растворенного вещества на 1 кг растворителя). Например, для воды коэффициент Кf равен 1,86 К.
Воспользовавшись классическим приближением (закон Рауля) для определения понижения температуры замерзания раствора проведем небольшое исследование. Учитывая, что природные растворы могут быть сильными электролитами, вывод расчетных выражений и численные оценки будут вестись так, чтобы без существенного изменения исходных формул, иметь возможность вносить квазиклассические поправки [2].
В качестве необходимых условий термодинамического равновесия раствора постулируем:
А) Изменение импульса локального объема раствора равно нулю 
; где m - масса элементарного, локального объема раствора; 
- скорость раствора.
Б) Флуктуации термодинамических параметров системы считаем пренебрежимо малыми при рассмотрении локального термодинамического равновесия раствора при фазовых переходах
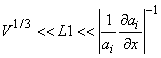
Здесь (L1)3 - элементарный физический объем; V - объем на одну частицу; ai - макроскопические параметры системы; τL2 - характерное время релаксации системы; τL1 - характерное время релаксации в объеме на одну частицу; τ - время релаксации в элементарном объеме.
В) Определяющее уравнение локального равновесия имеет вид:
.
При указанных условиях исследуем равновесие системы, состоящей из К = 2 компонент [растворимое вещество - соль (например, NaCl), растворитель - Н2О] и r = 2 фазы. Согласно правилу фаз Гиббса данная система обладает количеством степеней свободы равной 
. Следовательно, из четырех переменных Т, Р, Сж., Ств произвольные значения могут принимать только два параметра. Т.е. если заданы Сж (концентрация растворенного вещества в жидкой фазе) и Ств ( тоже в твердой фазе), то переменными величинами являются температура и давление.
Условие локального термодинамического равновесия означает равенство химических потенциалов в точке фазового перехода. Запишем это следующим образом:
(2)
где 
- химический потенциал воды; 
- химический потенциал льда.
Понятно, что для воды при отсутствии в ней растворенного вещества Сж = Ств = 0 равенство химических потенциалов будет иметь вид:
. (3)
На кривой локального термодинамического равновесия фаз температуре замерзания раствора ТЕ соответствует давление РЕ = Р(ТЕ).
Разложим химический потенциал μ в ряд Тейлора в точке замерзания раствора и удержим только первые три его члена.
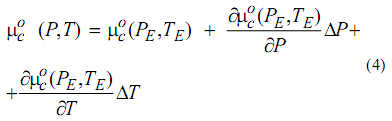(4)
Теперь, разложим условие локального равновесия (2), используя выражение (4) для химического потенциала:
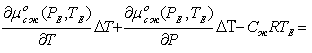
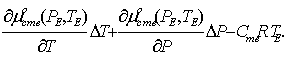(5)
Учитывая, что энергия Гиббса и химический потенциал связана между собой выражением 
, найдем:
,
. (6)
Подставим (6) в (5) получим:
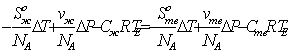(7)
Скрытая теплота в точке фазового перехода определяется через энтальпию следующим образом:
. (8)
Тогда, условие локального термодинамического равновесия (7) будет иметь вид:
(9)
При свободном замерзании раствора 
и если растворимое вещество не вымерзает градиент понижения температуры замерзания раствора определиться в виде:
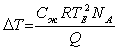. (10)
Концентрация растворенного вещества в жидкости определяется через отношение числа молекул растворителя и растворенного вещества. Отнеся теплоту плавления к 1 Кмоль, получаем:
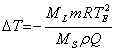. (11)
Например, если растворим 15 г соли NaCl в 1 л воды, то температура понижения замерзания раствора будет равна:
.
Водный раствор NaCl обладает свойствами электролита в зависимости от концентрации. Поэтому необходимо внести в выражение (11) поправочный множитель Дебая-Хюккеля, учитывающий взаимодействие ионов в электролите. При выводе поправки Дебая учитывалась только кулоновская часть термодинамического потенциала:
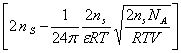. (12)
Тогда для водного раствора NaCl заданной концентрации для условий предыдущего примера получим:
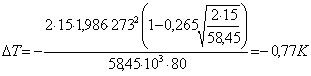
Поправка Дебая для температуры ΔТ в нашем случае дает два корня m1 = 0 и m2 = 416,2. В действительности, поправка Дебая работает только до точки экстремума (m = 184,9 и ΔТ = -3,9). Учет химической поправки может быть выполнен либо построением эмпирического термического уравнения состояния, либо расчетом фазового интеграла Гиббса.
Из условия локального равновесия непосредственно следует уравнение Гиббса для энтропии:
. (13)
Обозначим максимальную энтропию системы через величину Smax . Применим термодинамическую теорию возмущений к данной системе вблизи точки Smax . Характерное условие будет иметь вид:
.
В этом случае устойчивость энтропии системы будет определяться вариацией энтропии второго порядка δ2S , т.к. член первого порядка при приближении функции к максимальному значению обращается в нуль. Тогда, условие устойчивости имеет вид: 
.
Проанализируем уравнение Гиббса с помощью метода возмущения. Так как энтропия является аддитивной величиной, то каждую переменную уравнения рассмотрим отдельно, а общий результат суммируем. Тогда, критерий термодинамической устойчивости системы примет вид квадратичной формы:
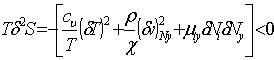(14)
где cu - теплоемкость; ρ - плотность; Χ - изотермическая сжимаемость; Ni - мольная доля компоненты i. Индекс Ny означает, что при вариации Ny состав раствора остается постоянным.
Основные условия устойчивости термодинамического равновесия подразделяются на следующие виды:
- тепловая устойчивость;
- механическая устойчивость;
- диффузионная устойчивость.
Физический смысл условий очевиден. Например, если нарушается тепловое условие устойчивости, то это приведет согласно уравнению Фурье не к затуханию, а к росту флуктуаций. Основное достоинство критерия (14) в его универсальности применения к растворам различного типа в мерзлых горных породах и грунтах.
Литература
- Петров Е.Е., Мордовской С.Д. Методы прогноза термомеханического состояния массива многолетнемерзлых горных породах. Якутск: ЯГУ, 1995. - 48 с.
- Ландау Л., Лифшиц Е. Статистическая физика. М.: Изд-во технико-теоретической литературы, 1951.- 480 с.