Теория краевых задач для вырождающихся гиперболических и смешанного типов уравнений является одним из важнейших разделов теории дифференциальных уравнений с частными производными. Интерес к таким уравнениям объясняется как теоретической значимостью получаемых результатов, так и многочисленными практическими приложениями в газовой динамике, теории бесконечно малых изгибаний поверхностей, в безмоментной теории оболочек, в магнитной гидродинамике, в теории электронного рассеивания, в математической биологии. Они имеют большое значение при математическом моделировании нефтяных пластов, фильтраций грунтовых вод, переноса тепла и массы в объекте, имеющего сложное строение, электрических колебаний в проводах и других областях.
Задачи со смещением существенно обобщают классические задачи для вырождающихся гиперболических и смешанного типов уравнений, имеют многомерные аналоги и содержат широкий класс корректных самосопряженных задач.
Цель исследования: доказать существование и единственность решения задачи со смещением для вырождающегося гиперболического уравнения.
Постановка задачи. Рассмотрим уравнение
|y|l uxx – uyy = 0, (1)
где l = m при y > 0 и l = n при y < 0, m, n –положительные постоянные, в конечной области Ω, ограниченной характеристиками AC, BC, AD, BD уравнения (1), выходящими из точек A(0, 0), B(1, 0).
Пусть Ω1 = Ω∩(y > 0), Ω2 = Ω∩(y < 0), J – интервал 0 < x < l прямой y = 0.
Задача. Найти решение уравнения (1)
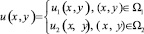
из класса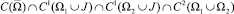 
, удовлетворяющее краевым условиям
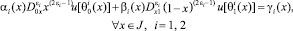(2)
и условию сопряжения
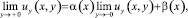(3)
где ε1 = m/(2m + 4), ε2 = n/(2n + 4);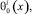 
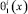– точки пересечения характеристик уравнения (1), выходящих из точки (x, 0) ∈ J, с характеристиками AC, AD, BC, BD соответственно αi(x), βi(x), γi(x), α(x), β(x) – заданные функции, причем
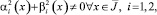
αi(x), βi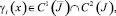(x), 
α(x),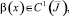 
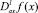– операторы дробного в смысле Римана – Лиувилля интегро-дифференцирования от функции f(х) [9].
Задача (1)–(3) относится к классу краевых задач со смещением [6]. При α2(x) = β1(x) = 0 существование и единственность решения задачи (1)–(3) были доказаны С.К. Кумыковой и Ф.Б. Нахушевой [2].
Единственность решения задачи
Пусть, как и принято, τ(x) = u(x, 0)
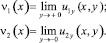
Выписывая решение задачи Коши для уравнения (1) в областях Ω1 и Ω2 [1], а затем, удовлетворив его краевым условиям (2), получим соотношения между τ(x) и νi(x), i = 1, 2
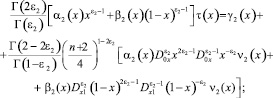(4)
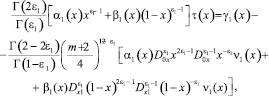(5)
принесенные на J из областей Ω1 и Ω2, где Γ(α) – гамма функция Эйлера [4].
Принимая во внимание равенства [3]
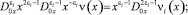
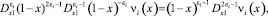
соотношения (5)–(4) перепишем в виде
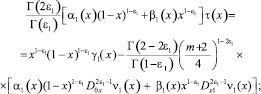(6)
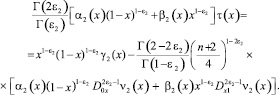(7)
Теорема. В области Ω не может существовать более одного решения задачи, если выполнено либо
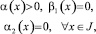(8)
либо
α(x) ≡ 1,
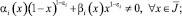(9)
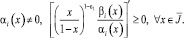(10)
Доказательство. При выполнении (8) единственность решения задачи (1)–(3) установлена в [2]. Докажем, что решение задачи единственно при выполнении условий (9), (10). Для этого покажем, что интеграл
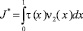
не может быть отрицательным.
Полагая γ2(x) = 0, перепишем (7) в виде
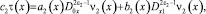
где
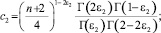
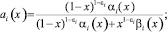
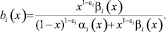
Рассмотрим интеграл
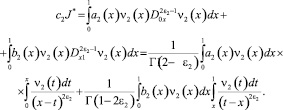(11)
Воспользуемся формулой [4] для гамма функции
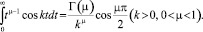
Полагая в ней k = |x – ξ|, μ = 2ε2, получим
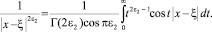
Откуда, поменяв порядок интегрирования в (11), будем иметь
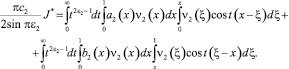
С учетом ai(1) = bi(0) = 0 , вычислениями, аналогичными [2], получим
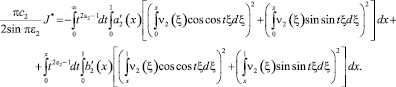(12)
Нетрудно видеть, что при выполнении условий теоремы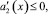 
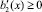и, следовательно, J* ≥ 0 .
При γ1(x) = 0 из (6) также получается неравенство
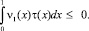
Так как при α(x) ≡ 1, β(x) ≡ 0, ν1(x) = ν2(x), то
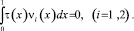
Таким образом, левая часть (12) равна нулю. Поскольку слагаемые справа неотрицательны, то они также равны нулю. В частности,
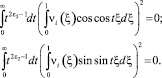
Так как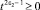 
, то
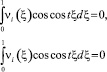
для всех t ∈ (0,∞), в частности, при t = 2πk, k = 0, 1, 2, … При этих значениях t функции sin tξ и cos tξ образуют полную ортогональную систему функций в L2.
Следовательно, νi(ξ) = 0 почти всюду, а так как они непрерывны по условию, то νi(ξ) = 0 всюду. Отсюда из (6), (7) при γi(x) = 0, i = 1, 2, заключаем, что τ(x) = 0 и, следовательно, ui(x, y) = 0 как решения задачи Коши в областях Ω1, Ω2 с нулевыми данными на J.
Существование решения задачи
Исключая τ(x) из (6) и (7), с учетом условия сопряжения (3), получим уравнение
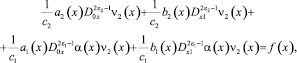(13)
где
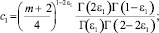
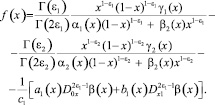
Пусть a2(x) ≠ 0. подействовав на обе части (13) оператором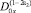 
, будем иметь:
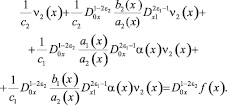(14)
Существование решения задачи исследовано в случаях m = n и n > m. При n > m уравнение (14) сведено к сингулярному интегральному уравнению [5]
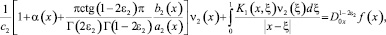(15)
а при n = m совпадает с сингулярным интегральным уравнением
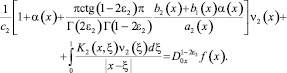(16)
Из свойств функций αi(x), βi(x), γi(x), α(x), β(x), i = 1, 2 , заключаем, что правая часть уравнений (15), (16) принадлежат классу C1(J), ,причем при x → 0 и x → 1 может обращаться в бесконечность порядка не выше 1 – 2εi. Ядра уравнений (15), (16)
.
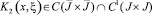Условие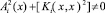 
гарантирует существование регуляризатора, приводящего уравнения (15), (16) к уравнению Фредгольма второго рода, где
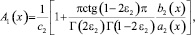
при n > m, а при n = m
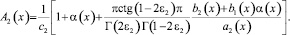
Из возможности приведения задачи к эквивалентному интегральному уравнению Фредгольма второго рода и единственности искомого решения следует существование решения поставленной задачи. По найденному ν2(x) можно найти ν1(x), а следовательно и τ(x). Решение задачи (1)–(3) может быть найдено как решение задачи Коши в областях Ω1 и Ω2.
Отметим, что задачи со смещением для уравнений гиперболического и смешанного типов с операторами обобщенного дробного интегро-дифференцирования исследовались в работах [7, 8].