Подземные хранилища газа (ПХГ) являются неотъемлемой частью единой системы газоснабжения не только России, но и соседних государств, взаимодействующих с Газпромом. Их роль весьма значительна и постоянно возрастает. Используются не только старые выработки, но строятся новые надежные ПХГ. Удобству их эксплуатации отвечает ряд соображений, возникающих [1] из сравнения с иными способами обеспечения потребления газа: они находятся вблизи объекта использования, что сказывается на времени доставки газа потребителю, позволяет регулировать сезонную неравномерность потребления газа, снижать пиковые нагрузки, обеспечивать гибкость и надежность поставок.
Вопросам обеспечения прочности и устойчивости подземных выработок [2], а также их крепей [3] уделяется существенное внимание. В настоящей работе ставится целью прогнозирование результатов механического взаимодействия полостей (ПХГ). Для ее достижения намечены и реализованы следующие задачи: выбор метода решения (МГСВ – новый энергетический метод граничных состояний в сочетании с возмущениями) [4]; постановка и решение ряда задач (формирование граничных условий (ГУ), обезразмеривание, обеспечение решения); оценка характеристик прочности и устойчивости; выработка рекомендаций.
Метод граничных состояний – эффективное средство решения многополостных задач
В МГС (методе граничных состояний) [5] под состоянием среды понимается согласованный набор ее характеристик. В случае изотропной упругости ее состояние в области V описывают [6] соотношения Коши
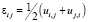 , (1.1)
, (1.1)
обобщенный закон Гука
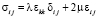 , (1.2)
, (1.2)
уравнения равновесия
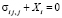 , (1.3)
, (1.3)
где ui – компонента вектора перемещения, σij, σij – компоненты тензоров напряжений и деформаций, λ, μ – параметры Ламе (в общем случае неоднородные), Xi – объемные силы, δi – символ Кронекера. Тогда внутреннее состояние есть непротиворечивый набор 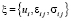 , отвечающий уравнениям (1.1)–(1.3).
, отвечающий уравнениям (1.1)–(1.3).
Внутреннее состояние ξ индуцирует соответствующее граничное состояние 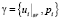 ,
, 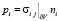 , где ni – компонента единичного вектора внешней нормали к границе ∂V. В силу теоремы Сомильяны [7], принципа возможных перемещений и линейности определяющих соотношений изоморфизм ξ↔γ является гильбертовым. Для обеспечения ортогонализации вводятся скалярные произведения:
, где ni – компонента единичного вектора внешней нормали к границе ∂V. В силу теоремы Сомильяны [7], принципа возможных перемещений и линейности определяющих соотношений изоморфизм ξ↔γ является гильбертовым. Для обеспечения ортогонализации вводятся скалярные произведения:
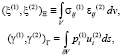
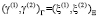
в пространствах 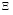 и Г, составленных из возможных реализаций состояний ξ, γ соответственно.
и Г, составленных из возможных реализаций состояний ξ, γ соответственно.
Атрибуты результирующих состояний изоморфных гильбертовых пространств представляются соответственно рядами Фурье по элементам ортонормированных базисов (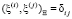 ):
):
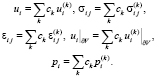 (1.4)
(1.4)
Соотношения (1.1)–(1.3) составляют задачу линейной неоднородной эластостатики, для которой из-за функционального наполнения коэффициентов Ламе общее решение отсутствует. Декомпозиция методом А. Пуанкаре приводит к последовательности линейных задач эластостатики с постоянными коэффициентами.
Решение задачи каждого приближения состоит в определении коэффициентов Фурье из информации, содержащейся в ГУ. МГС эффективно решены многие основные и смешанные задачи эластостатики для односвязных тел. В последнее время МГС эффективно развит в части решения задач для многосвязных тел. К настоящему времени – задачи для неограниченного тела с полостями и включениями: о взаимовлиянии сферических полостей (1-я основная), о взаимовлиянии сферических включений (2-я основная) [8], о взаимодействии полости и включения (основная смешанная) [8]; для ограниченного тела: сферический слой (осевая симметрия), сферический слой в шаре при различных нагружениях, сжатие кругового цилиндра, содержащего сферическую полость, задача о кубе со сферическими полостями.
Методология решения задач средствами МГС определена [4]. Выполним декомпозицию определяющих соотношений эластостатической среды методом А. Пуанкаре. Будем искать искомое состояние в виде разложения 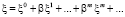 по малому параметру . Считая ГУ отнесенными к состоянию 0, приходим к последовательности задач изотропной эластостатики:
по малому параметру . Считая ГУ отнесенными к состоянию 0, приходим к последовательности задач изотропной эластостатики:
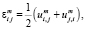
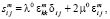
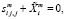
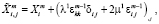 (1.5)
(1.5)
где
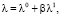
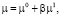
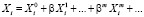 ,
,
а 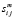 на шаге m формально выполняет роль компоненты тензора напряжений и строится по решении задачи итерации m. Тогда реальный тензор напряжений есть
на шаге m формально выполняет роль компоненты тензора напряжений и строится по решении задачи итерации m. Тогда реальный тензор напряжений есть
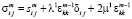 . (1.6)
. (1.6)
Одна из положительных особенностей использования МГС в контексте метода возмущений состоит в том, что поставленные ГУ достаточно удерживать лишь при итерации m = 0, а для последующих итераций достаточно решить первую или вторую основные задачи, поскольку в этих случаях построение решения сводится к рутинному подсчету квадратур. В приближении m общее решение для односвязного ограниченного либо неограниченного тела представляется решениями Аржаных – Слободянского (1.7), (1.8) соответственно:
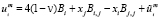 , (1.7)
, (1.7)
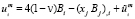 , (1.8)
, (1.8)
где 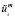 – известная величина как составляющая перемещения, обусловленная объемными силами
– известная величина как составляющая перемещения, обусловленная объемными силами 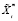 ;
; 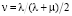 – коэффициент Пуассона, Bi – компонента произвольного гармонического вектора. Общие решения (1.7), (1.8) служат эффективно, формируя базис пространства состояний для тела.
– коэффициент Пуассона, Bi – компонента произвольного гармонического вектора. Общие решения (1.7), (1.8) служат эффективно, формируя базис пространства состояний для тела.
Выражения (1.5), (1.6) показывают, что на каждом шаге итерации при решении неоднородной задачи формально возникают фиктивные неконсервативные объемные силы. Учет объемных сил непотенциального характера реализован и состоит в восстановлении внутреннего и ему соответствующего граничного состояний, обусловленных лишь этими силами.
Постановка задач о взаимодействии сферических полостей в коре земного шара
Для организации искусственных ПХГ реально достижимым является слой осадочных пород (осадочная оболочка глубиной до нескольких километров), перемежающихся с выступами гранитной оболочки, углубляющейся до десятков километров [9]. Слои базальтовый (до 30 км) и сиалевый (50–60 км) для практических целей пока технически не достижимы. Реальным окружением для ПХГ разумно считать пласты гранита, расположенные ближе к поверхности земного шара. Модуль сдвига гранита в нормальных условиях составляет величину порядка 1,6•104 МПа, коэффициент Пуассона зависит от структуры гранита и колеблется в пределах 0,1–0,15. Для осадочных пород он наблюдается в пределах 0,15–0,38 [10]. Учитывая перемеженность фракций гранита с прочими породами у поверхности земного шара, при расчетах будем принимать значение коэффициента равным 0,15 и считать его постоянным в верхнем слое коры глубиной до 0,5 км, в то время, как модуль сдвига возрастает с ростом давления [10]; давление у подошвы земной коры (около 50 км) составляет около 13 тысяч атмосфер, следовательно, линейная оценка изменения избыточного давления в земной коре по глубине h дает зависимость p ≈ 0,26h атм. [9]. Справочные данные указывают качественно на прямую зависимость модуля сдвига от давления, но не уточняют количественную сторону дела [9], поэтому модуль сдвига и ему соответствующий модуль объемного деформирования при выбранном значении коэффициента Пуассона будем оценивать посредством параметра β в виде 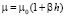 ,
, 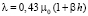 .
.
Учитывая практическую сторону организации ПХГ и рекомендованную глубину их расположения (от 100 до 1500 м) [10], рассмотрим задачу о взаимодействии двух сферических ПХГ, выполненных в гранитном слое толщиной R0 = 300 м на глубине h0 = 100 м радиусом r0 = 50 м. Анализируемую область ограничим цилиндрической поверхностью радиуса R0; ось цилиндра расположена симметрично относительно выработок, центры обеих полостей отстоят от осей на расстоянии h0. Толщина верхнего слоя до границы выработки назначена не очень значительной специально для того, чтобы отследить влияние полостей на состояние приповерхностного слоя. Напротив, нижняя грань слоя и цилиндрическая граница рассматриваемой области удалены от границ выработок на более значительные расстояния, чтобы наличие полостей мало искажало значение давления (в соответствии с принципом Сен-Венана) на искусственно выделенной границе.
В безразмерной постановке с масштабными коэффициентами по напряжениям μ0 и по геометрии R0 задача сводится к определению напряженно-деформированного состояния (НДС) для неоднородной эластостатической среды, заключенной внутри цилиндра радиуса 1 и высотой 1, простирающейся по оси z в пределах 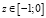 . Начало координат расположено на верхней грани, так что плоскость Oxy касается поверхности земного шара. Центры сфер радиусами 1/6 суть
. Начало координат расположено на верхней грани, так что плоскость Oxy касается поверхности земного шара. Центры сфер радиусами 1/6 суть 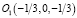 ,
, 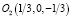 (рисунок).
(рисунок).
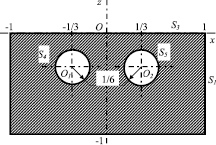
Сечение y = 0 анализируемого слоя осадочной породы с полостями
ГУ отвечают постановке первой основной задачи, а именно граница S3 свободна от нагрузки, на границе S2 действует нормальное давление p2 = 0,0005, на границе S1 давление меняется по закону –0,0005z, z < 0. Границы S4, S5 полостей предполагается загрузить тремя способами:
1) обе границы свободны от давления,
2) S4 свободна от нагрузки, по S5 действует давление p5 = 0,0016,
3) обе полости нагружены максимальным давлением p4 = p5 =0,0016.
Неоднородность механических свойств учитывалась малым параметром β: 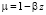 ,
, 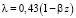 , ν = 0,15. Решение задачи проводилось средствами МГС, обвязанного методом возмущений при значениях
, ν = 0,15. Решение задачи проводилось средствами МГС, обвязанного методом возмущений при значениях 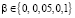 .
.
Для каждой задачи выполнялось три итерации. Сходимость решения на каждой итерации оценивалась как косвенно (отслеживание насыщения суммы Бесселя), так и напрямую через среднеквадратичную интегральную невязку решения с ГУ. Для учета НДС, обусловленного объемными силами, искусственно порождающимися в итерационном процессе метода возмущений в соответствии с (1.5), использовался алгоритм, исходящий из существования счетного базиса сил, единственной компонентой которых является моном от x, y, z, размещенный в поочередно в каждой позиции вектора X.
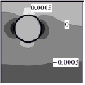
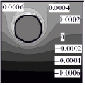
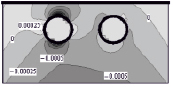
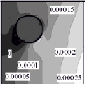
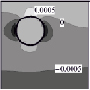
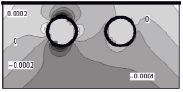
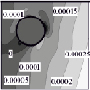
Результаты решения средствами МГС построены в аналитическом виде, но ввиду необозримости символьных выражений представлены в графической форме (табл. 1–2, линии уровня напряжений). Нулевой уровень напряжений соответствует фону (внутренность полостей), более высоким значениям соответствуют более светлые тона. На рисунках, помещенных в формат таблиц, представлены напряжения в сечении y = 0; в случае задач 1), 3), обладающих симметрией в постановке, удержано ограничение x > 0.
Таблица 1
Опорное линейное напряженное состояние (β = 0)
|
Незагруженные полости
|
Одна загруженная полость
|
Загруженные полости
|
|
|
σxx |
|
|
|
|
σyy |
|
|
|
|
σzz |
|
|
|
|
σxz |
|
|
|
Таблица 2
Возмущенное напряженное состояние (β = 0,1)
|
Незагруженные полости |
Одна загруженная полость |
Загруженные полости |
|
|
σxx |
|
|
|
|
σyy |
|
|
|
|
σzz |
|
|
|
|
σxz |
|
|
|
Анализ напряжений σxx, σyy, σzz, σxz и их сопоставление между постановками показывают:
1) радиальные (по отношению к цилиндрической форме внешней границы целика) напряжения σxx достигают своего положительного максимума в верхних полюсах сферических полостей;
2) окружные (σyy) также имеют приоритетные значения в «северных полюсах»;
3) характер осевых (σzz) напряжений существенно зависит от ГУ и взаимовлияния полостей, но по уровню уступает комбинации σxx ~ σyy, ориентированной на разрыв волокон, примыкающих к полостям;
4) сдвиговые напряжения (σxz) в окрестности полости в существенной степени определяются именно нагружением этой полости.
Эти соображения позволяют сформировать критерий, по которому можно судить об опасности образования трещин нормального отрыва в волокнах, примыкающих к полостям, а именно: в качестве коэффициента концентрации напряжений логично выбрать величину
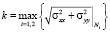 ,
,
где «северные полюсы» полостей N1,2 имеют координаты 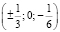 .
.
В табл. 3 сопоставлены значения коэффициента k при различных предельных случаях функционирования ПХГ и варьируемых значениях параметра β.
Таблица 3
Критерий разрушения (коэффициент концентрации напряжений k)
|
β,×10-3 |
Незагруженные полости |
Одна загруженная полость |
Загруженные полости |
|
0 |
0,35 |
1,52 |
1,70 |
|
0,05 |
0,41 |
1,57 |
1,70 |
|
0,1 |
0,46 |
1,61 |
1,70 |
Из сопоставления значений видно, что наибольшую опасность в плане возникновения разрушения представляет собой вариант, когда обе полости загружены максимальным давлением.
О корректности построенных решений можно судить по интегральной среднеквадратической невязке ГУ с построенным граничным состоянием. Соответствующая информация помещена в табл. 4. Этого достаточно для констатации корректности решения, поскольку суммарное внутреннее состояние удовлетворяет тождественно соотношениям (1.5) на каждом шаге итерации. Таким образом, сходимость итерационного процесса и достоверность решения показана во всех трех постановках.
Таблица 4
Оценка достоверности решения (невязка)
|
β,×10-3 |
Незагруженные полости |
Одна загруженная полость |
Загруженные полости |
|
0 |
0,89 |
0,91 |
0,88 |
|
0,05 |
0,90 |
0,91 |
0,88 |
|
0,1 |
0,92 |
0,93 |
0,89 |
Максимальное значение коэффициента концентрации напряжений k = 0,00170, которому с учетом масштаба по напряжениям μ0 = 1,6•104 МПа, позволяет проектировать усиливающие элементы ПХГ, локализуемые в верхних полярных шапках полостей (разумеется, с назначаемыми конструкторами коэффициентами запаса прочности).
Работа выполнена при поддержке гранта РФФИ № 16-41-480729 «р_а».