В настоящей работе на основе этой функции выведены законы теории поля. Пусть функция состояния для системы «заряженная частица - поле» имеет вид:
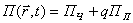 (1)
(1)
где ПЧ - функция состояния свободной частицы, ПП - функция состояния поля.
При изменении состояния системы П - функция меняется на величину dП и из условия для полного дифференциала получаем выражение для силу, действующую на частицу стороны поля [1].
![]() ,
,
где ![]() (2)
(2)
![]() (3)
(3)
Векторы поля 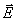 и
и ![]() задаются с точностью до преобразования калибровки.
задаются с точностью до преобразования калибровки.
![]() (4)
(4)
Преобразование калибровки есть прямое следствие преобразования функции состояния.
![]() (5)
(5)
Произвол выбора χ - функции позволяет выбрать
□ ПП =0. (6)
Этот результат так же независимо следует для свободного электромагнитного поля из принципа дальнодействия [2]. В раскрытом виде выражение (6) есть не что иное, как условие Лоренца для потенциалов свободного электромагнитного поля.
□![]()
![]() (7)
(7)
Уравнение (2) с учётом (4) позволяет получить два уравнения Максвелла для 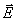 и
и ![]() .
.
![]() (8)
(8)
Взяв производные от выражения (7), соответственно по времени и по координатам с учётом обозначения (3), можно получить уравнения для скалярного и векторного потенциалов в вакууме.
□φ=0
□![]() =0
=0
Для того, чтобы получить уравнения для поля с источниками необходимо в теорию «руками» внести закон взаимодействия зарядов (закон Кулона) в дифференциальной форме, имеющей вид
![]()
Мы будем исходить не из принципа необходимости, а из принципа достаточности, для чего введем в рассмотрение функцию состояния для распределенных зарядов S. Определим:
![]() (8)
(8)
Из условия □S=0, подставляя обозначения (8), мы получаем уравнение непрерывности (закон сохранения заряда):
![]() (9)
(9)
Если величина заряда определяется из закона Кулона, то плотность тока можно определить из интегральной формы уравнения непрерывности
![]()
Отсюда следует, что закон сохранения заряда есть прямое следствие существования зарядовой функции состояния S. Примем, что уравнение для ПП-функции в точках, где имеются источники, имеет вид:
□ПП =S (10)
Взяв производную по времени от обеих частей этого уравнения и, независимо, производную по координатам этого же уравнения, мы получаем уравнение для скалярного и векторного потенциалов с источниками:
□ ![]() (11)
(11)
□ ![]() (12)
(12)
Складывая их производные от этих выражений соответственно по r и по t, получаем выражение:
□□ ![]() □
□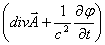 =□S=
=□S= ![]()
из которого видно, что уравнение непрерывности следует также из условия Лоренца для потенциала поля. В результате мы получили полную систему (3,11,12) уравнений для электромагнитного поля, не привлекая при этом к выводу этих уравнений первого уравнения Максвелла. Вместо него нами была использована зарядовая функция состояния и уравнение непрерывности.
Наш вывод уравнений электродинамики, основанный на введении функции состояний для поля и для распределенных зарядов источников этого поля, позволяет не только вывести сами уравнения Максвелла, но и сделать ряд важных выводов.
Об одном из них, о природе закона сохранения зарядов, сказано выше. Но, пожалуй, наиболее любопытный вывод заключается в том, что свободное электромагнитное поле в вакууме отсутствует
![]()
аналогично
![]()
Это соответствует известному факту, что фазовая скорость электромагнитной волны в пустоте энергии не несет, и напрямую следует из принципа дальнодействия [2]. Использование в ряде практических задач свойство свободных электромагнитных волн является хорошо разработанной схемой для решения практических задач в рамках теории близкодействия. Если электродинамика, основанная на принципе близкодействия, прекрасно разработана, то использование принципа дальнодействия пока еще не получило развития, хотя ряд задач в этом случае решается значительно проще и понятнее. Ведь, по сути, не длины волн определяют электромагнитные взаимодействия, а частоты колебаний зарядов источника. Заметим, что уравнение непрерывности есть следствие существования зарядовой функции состояния [2].
СПИСОК ЛИТЕРАТУРЫ:
- Журнал «Успехи современного естествознания» №7, М.: 2008, стр.9-12.
- Журнал «Современные наукоёмкие технологии» №7, М.: 2008 стр.9-12.



