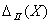Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Файлы

Кондратенко А.В. Вараксин М.Ю. Бабак Л.И.

Статья в формате PDF

144 KB

Процесс разработки фильтров СВЧ в последнее время существенно усложнился из-за возрастания сложности новых систем и необходимости более тщательного и точного проектирования. Предъявляемые требования зачастую оказываются противоречивыми, поэтому проектирование представляет собой многокритериальную задачу. Вопрос еще более усложняется из-за того, что возможности подстройки и регулировки некоторых устройств после изготовления ограничены либо полностью отсутствуют. Данные обстоятельства привели к тому, что автоматизированное проектирование стало неотъемлемым этапом разработки фильтров СВЧ. Современные системы автоматизированного проектирования (САПР) устройств СВЧ можно условно разделить на две основные группы:

1. Программы, которые базируются на электрических моделях и эквивалентных схемах. Использование данных программ целесообразно в тех случаях, когда может быть составлена эквивалентная схема, в достаточной степени соответствующая реальному устройству. При этом неидеальность используемых моделей во многих случаях можно учесть путем введения подстроечных элементов на этапе проектирования.

2. Программы, в которых задача анализа решается на электродинамическом уровне. Данная группа программ традиционно делится на две категории: 2D - моделирующие программы, предназначенные для анализа только непрерывных структур, бесконечных в одном направлении, и 3D - моделирующие программы, способные анализировать практически любую объемную структуру с высокой точностью, но требующие значительных временных и вычислительных ресурсов.

Требования к точности проектирования фильтров СВЧ высоки и, по-видимому, во многих случаях могут быть удовлетворены только в рамках многомерного электродинамического анализа. Поэтому весьма актуальным является использование такого подхода к проектированию, который бы обеспечивал высокую точность при небольших затратах временных и вычислительных ресурсов. Одним из таких подходов является использование нейронных сетей [1].

Идея использования нейронной сети заключается в том, что после затрат времени на обучение на основе совокупности характеристик устройства, полученных в результате электродинамического (ЭД) моделирования, нейромодель имитирует свойства данного устройства. При ее использовании можно значительно сократить время, необходимое для анализа и оптимизации.

Нейронное моделирование проводилось в пакете NeuroModeler 1.2.2. В качестве объекта обучения выбран трехслойный персептрон, представляющий собой нейронную сеть с тремя слоями нейронов: входным, промежуточным (скрытым) и выходным. Входными (управляемыми) параметрами сети выбраны геометрические параметры фильтра (длины резонаторов (r1, r2) и диафрагм (d1, d2)). В качестве выходных параметров нейронной сети выбрана следующая совокупность критериев:

- центральная частота полосы пропускания ( );

- ширина полосы пропускания ( );

- минимальное значение коэффициента передачи в полосе пропускания ( );

- неравномерность коэффициента передачи в полосе пропускания ( );

- максимальное значение коэффициента отражения в полосе пропускания ( );

- уровень затухания при заданных отстройках от центральной частоты ( , ).

В качестве обучающих примеров использовалась выборка, представляющая собой совокупности значений критериев, вычисленных из результатов ЭД анализа при вариациях геометрических параметров. Каждый из четырех управляемых параметров мог принимать три различных значения, таким образом, расчет проводился для 81 комбинации значений параметров. Выбор небольшого количества обучающих примеров был сделан с целью сокращения суммарного времени расчета (время, необходимое для однократного ЭД анализа характеристик фильтра с точностью не хуже 1%, составляет порядка тридцати минут).

Для получения обучающей выборки в среде программирования Delphi была написана вспомогательная программа, которая, исходя из результатов ЭД анализа, производила расчет значений критериев, подготовку данных для пакета NeuroModeler, а также предоставляла возможность тестирования обученной нейромодели. Обобщенные сведения о структуре используемой нейронной сети приведены в табл. 1.

Таблица 1. Обобщенные сведения о структуре используемой нейронной сети.

В табл. 2 представлены относительные значения максимальных ошибок  по каждому критерию, полученные в результате тестирования нейромодели на примерах участвовавших в обучении.

Таблица 2. Тестирование нейронной модели на примерах, участвовавших в обучении.

В табл. 3 представлены относительные и абсолютные значения ошибок предсказания (  и ), полученные для трех вариаций значений геометрических параметров, не участвовавших в процессе обучения.

Таблица 3. Тестирование нейронной модели на примерах, не участвовавших в обучении.

Из табл. 3 видно, что максимальные ошибки соответствуют критериям  и . Абсолютные значения ошибок могут быть сравнимы с погрешностями измерения параметров реального устройства. Таким образом, точность нейромодели после обучения можно считать достаточной для практических применений.

После тестирования нейронная модель была экспортирована из пакета NeuroModeler в виде файла с расширением С. Для анализа и оптимизации частотных характеристик фильтра нейронная модель в виде DLL-файла подключена к системе визуальных вычислений Image.

В основу системы Image положены концепции «визуальных вычислений» и «визуального проектирования» (последний термин используется применительно к разработке технических объектов) [2, 3]. Главной особенностью реализованного в данной системе подхода является то, что он позволяет получить в принципе полное множество допустимых решений задачи. Это качество особенно ценно при решении систем неравенств, задач одно- и многокритериальной оптимизации, задач проектирования технических объектов и т.д. При этом пользователю предоставляется возможность задавать значения управляемых параметров, визуально контролировать допустимые области изменения этих параметров и все выходные критерии. В результате может быть получен набор наиболее приемлемых альтернативных решений, учитывающий как формализуемые, так и неформализуемые критерии.

Для решения задачи оптимизации к значениям критериев предъявлены следующие требования:

; ;

; ; ; ; .                       (1)

Ограничения на управляемые параметры (в миллиметрах):

; ; ; .                          (2)

Совокупность ограничений (1) и (2) задает область допустимых значений (ОДЗ) D_X в четырехмерном пространстве. Двумерные проекции области D_X на различные плоскости управляемых параметров позволяют определить в принципе все допустимые значения управляемых параметров.

Предварительный анализ показал, что наибольшей чувствительностью к изменению управляемых параметров обладают критерии  и , поэтому именно для них решалась задача оптимизации. Частота настройки фильтра полагалась равной 36 ГГц.

С использованием линий уровня критериев  и  выбраны значения переменных r1(1) и r2(1), принадлежащие проекции ОДЗ на плоскость управляемых параметров r1 и r2, которые одновременно обеспечивают минимальные потери и неравномерность коэффициента передачи в полосе пропускания фильтра. Затем на плоскости оставшихся свободных параметров d1, d2 при выбранных значениях r1(1) и r2(1) выбраны значения d1(1) и d2(1). Набор значений параметров  является решением. Задача оптимизации может быть аналогично решена для любых других критериев.

Для проверки достоверности результатов, полученных в системе Image, в программе трехмерного ЭД моделирования проведен анализ фильтра. В табл. 4 приведены значения критериев, полученные в системе Image (прогнозируемые величины) и в результате электродинамического расчета, а также абсолютные и относительные значения ошибок прогнозирования, полученных по каждому критерию.

Таблица 4. Результаты сравнительного анализа.

Как видно из табл. 4, абсолютные значения ошибок для критериев   являются незначительными, а для критериев   - пренебрежимо малыми. Можно утверждать, что совокупность данных погрешностей в целом не изменяет качества фильтрации.

СПИСОК ЛИТЕРАТУРЫ

1. M. H. Bakr, J. W. Bandler, M. A. Ismail, "Neural space-mapping optimization for EM-based design," IEEE Trans. Microwave Theory Tech., vol. 48, pp. 2307-2315, December 2000.
2. Бабак Л.И. Л.Поляков А.Ю. Система визуальных вычислений Image для решения математических и технико-экономических задач//Докл. междунар. симп. СИБКОНВЕРС´99. - Томск, 1999.
3. Бабак Л.И., Поляков А.Ю. Design Problem Solver - программа для решения задач проектирования технических устройств и систем. Основные концепции// Докл. междунар. симп. СИБКОНВЕРС´97.-Томск, 1997. С. 218- 228.

Библиографическая ссылка