Работа является продолжением исследований по классической проблеме математической физики, получившей название задачи Стефана. Строится и анализируется на основе развитого одним из авторов метода [1,2] математическая модель задачи о плавлении одномерного твердого материала, учитывающая конечную скорость распространения тепла (гиперболический закон теплопроводности; см. [3]) и скачки температуры и теплового потока на границе раздела фаз; см. [4]. Возникающая при моделировании краевая задача со свободной границей после перехода к безразмерным величинам и затем - к римановым инвариантам имеет следующий вид. Ищутся константа t* > 0 , гладкая функция φ( t ) на [0,t*], φ(0) = 0, φ >0 при t >0, и гладкие функции u1(x), u2(x) в области ![]() , такие, что выполняется равенство:
, такие, что выполняется равенство:
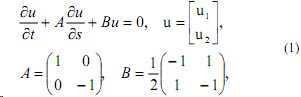
и при этом функции 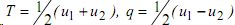 и их предельные значения на границе D удовлетворяют условиям T>0, q>0,
и их предельные значения на границе D удовлетворяют условиям T>0, q>0,
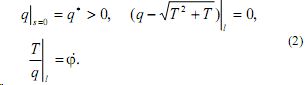
Здесь l = {x:s =φ(t)}- граница раздела фаз, T,q - безразмерные температура и тепловой поток в жидкой фазе.
Доказана однозначная разрешимость краевой задачи (1)-(2), получены оценки для константы t* и порогового значения q* , предложена итерационная процедура построения функций φ , T , q Центральным местом в обосновании является построение и анализ интегрального уравнения для предельного значения температуры жидкой фазы на границе раздела фаз.
Заметим, что с учетом φ(0) = 0 кривая l лежит при t > 0 в открытом углу между прямой s = 0 и характеристикой s = t системы (1). Это означает выполнение в данной модели физического требования: граница раздела фаз движется не быстрее фронта тепловой волны [5].
ЛИТЕРАТУРА. [1] Романовский Р.К.// Мат.сб. 1987. Т.133, № 3. С. 341-355. [2] Воробьева Е.В., Романовский Р.К. // Сиб. матем. журн. 2000.Т.41, № 3, С. 531-540. [3] Соболев С.Л. // УФН. 1997. Т.167, № 10. С. 1095-1106. [4] Соболев С.Л. // УФН. 1991. Т.161, № 3. С.5-29. [5] Лыков А.В. // Инж.-физ. журн. 1965. Т.9, № 3. С. 287-304.
Библиографическая ссылка
Романовский Р.К., Стратилатова Е.Н. Гиперболическая модель задачи о фазовом переходе // Успехи современного естествознания. 2003. № 11. С. 99-100;URL: https://natural-sciences.ru/ru/article/view?id=15324 (дата обращения: 18.01.2026).



