Моделирование процессов в химических реакторах в ряде случаев приводит к краевым задачам для гиперболических уравнений [1-5]. В частности, процесс в реакторе с кипящим слоем катализатора при реакции первого порядка (скорость реакции линейно зависит от концентрации реагирующего вещества) моделируется [1] смешанной задачей для почти линейной гиперболической системы на плоскости
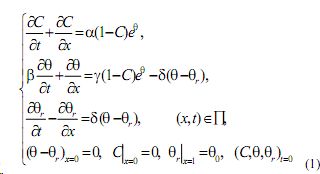
Здесь П - полуполоса (0,1) (0, ∞),θ, θr - температура в реакторе и холодильнике, Ñ - концентрация реагирующего вещества, α, β, γ, δ, θ0 - постоянные, из них первые четыре положительны, начальные функции – гладкие и удовлетворяют условиям согласования нулевого и первого порядков.
В данной работе установлено прямым методом Ляпунова достаточное условие экспоненциальной устойчивости в L2 - норме стационарного решения задачи (1) (вариант этого метода применительно к указанному классу краевых задач предложен в [5]), предварительно получено достаточное условие существования таких решений.
Теорема 1. Для существования хотя бы одного стационарного решения краевой задачи (1) достаточно выполнение неравенства
![]()
Пусть выполнено условие (2) и 12 ( z, v1,v2) - стационарное решение краевой задачи (1). Введем вектор отклонений
u = (C-z, θ - v1, θ - v2)
Будем говорить, что стационарное решение задачи (1) экспоненциально устойчиво в L2 - норме, если существует такое δ > 0 , что для решений (C, θ, θr) задачи (1) таких, что |u (x ,0)| < δ при x € при [0,1] , выполняется оценка
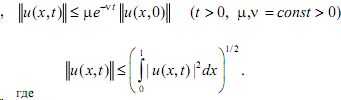
Теорема 2. Для экспоненциальной устойчивости в L2 - норме стационарного решения краевой задачи (1) достаточно выполнение неравенства
![]()
Отметим, что из (3) следует условие (2) существования стационарного решения.
В основе подхода к обоснованию лежит вариант прямого метода Ляпунова для гиперболических смешанных задач, предложенный в работе [5].
Литература
- Зеленяк Т.И. К вопросу об устойчивости решений смешанных задач для одного квазилинейного уравнения //Дифференц. уравнения. 1967. Т.3. №1. С.19-29.
- Шеплев В.С., Мещеряков В.Д. Математическое моделирование реакторов с кипящим слоем катализатора //В кн.: Математическое моделирование химических реакторов. Новосибирск: Наука. Сиб. Отд. 1984. С.44-65.
- Иванов Е.А. Управление процессом в реакторе с псевдоожиженным слоем //Там же. С.116-127.
- Акрамов Т.А. Качественный и численный анализ модели реактора с противотоком компонентов //Математическое моделирование каталитических реакторов. Новосибирск: Наука. 1989. С.195-214.
- Романовский Р.К., Воробьева Е.В., Макаро- ва И.Д. Об устойчивости решений смешанной задачи для почти линейной гиперболической системы на плоскости // Сиб. журн. индустр. математики. - 2003.- Т.6 - № 1. – С. 118-124.
Библиографическая ссылка
Макарова И.Д. Об устойчивости стационарных режимов в реакторе с кипящим слоем катализатора // Успехи современного естествознания. – 2003. – № 12. – С. 82-83;URL: https://natural-sciences.ru/ru/article/view?id=15580 (дата обращения: 26.04.2024).



