Теорема. Если a, b,c - положительные целые числа, то
an + bn ≠ cn , (1) при n ≥ 3 (1)
где n - целое положительное число.
Доказательство. Геометрической интерпретацией и анализом свойств функции
![]()
установлено, что любым x, y соответствует пара образующих чисел f , g
![]() где
где ![]()
Отсюда при независимых f,g следует:
x = f - g, y = 2 √fg (4)
Тогда (2) принимает вид:
![]()
При целых x = a, y = b, α = n, соответсвующих теореме
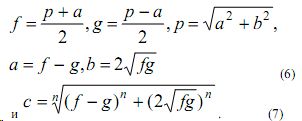
В общем случае a, b - целые числа, если f ,g - суть иррациональные числа порядка квадратного корня из суммы квадратов двух целых чисел. Числами Пифагора ( a = a pf, b = b pf ) они являются, когда квадратам целых чисел равны: а) f ,g (например,f =9, g = 4, a pf нечетно) или б) 2f, 2g,( f=24,5, g = 4,5, apf четно).
Особенность (7) состоит в том, что от характера p (иррациональное оно или целое) не зависит вид подкоренного выражения. Во всех случаях основания степеней слагаемых представлены целыми числами, и случай Пифагора в этом отношении не является особым.
Выражение (7) от радикала степени n освобождается при n = 2 (не считая, разумеется, n = 1 ), и тогда c = f + g = p . После этого при f,g соответствующих целым a,b число c может избавиться от иррациональности и стать целым только в случае чисел Пифагора (a = a pf, b = b pf, c = c pf)
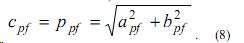
Таким образом, теорема доказана.
Из сказанного вытекает более общая теорема, в отношении которой последняя теорема Ферма является частным случаем [1]: уравнение an +bn = cn c abc ≠ 0 при n ≥1 , кроме n =1;2 , не имеет рациональных решений, то есть является иррациональной моделью взаимосвязанных чисел.
Она справедлива также для сопряженного уравнения an - bn = cn , которое с перестановкой членов ( an =bn + cn ) является прообразом рассмотренного.
Литература
- Соколов, Г.М. Функция z =α√xα + yα . Последняя (великая) теорема П. Ферма (элементарное доказательство) /Г.М. Соколов. – Йошкар-Ола, 2003. – 20с.
Библиографическая ссылка
Соколов Г.М. Образующие числа. Последняя теорема Ферма // Успехи современного естествознания. 2003. № 12. С. 130-130;URL: https://natural-sciences.ru/ru/article/view?id=15618 (дата обращения: 18.11.2025).



