Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Медведев А.В. 1

---

1 ФГБОУ ВПО «Российский экономический университет имени Г.В. Плеханова»

В статье описаны некоторые проблемы, системная концепция и инструменты моделирования и анализа задач бизнес-планирования в виде триады: математическая модель, операционный метод их исследования и автоматизированная информационно-аналитическая система. Основными особенностями комплекса являются использование алгоритмов построения производственных функций бизнес-процессов, учитывающих принятые основные бухгалтерские правила учета доходов и затрат, концептуальная ориентация на использование стандарта оптимизационных математических моделей в форме многокритериальных много- и одношаговых задач линейного программирования и соответствующих алгоритмов и методов их анализа и расчета. Делается вывод о создании полноценной системы поддержки принятия решений в сфере бизнес-планирования.

Статья в формате PDF

2476 KB

оптимизационный метод

многошаговая задача линейного программирования

автоматизированная информационно-аналитическая система

система поддержки принятия решений

1. Горбунов М.А. Вопросы математического моделирования и автоматизированной оценки эффективности инновационно-инвестиционных проектов / М.А. Горбунов, А.В. Медведев // Фундаментальные исследования. – 2014. – № 9(9). – С. 2044–2047.

2. Медведев А.В. Применение z-преобразования к исследованию многокритериальных линейных моделей регионального экономического развития. Монография / А.В. Медведев. – Красноярск: Изд-во СибГАУ имени академика М.Ф. Решетнева. – 2008. – 228 с.

3. Медведев А.В. Концепция оптимизационно-имитационного бизнес-планирования / А.В. Медведев // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 1. – Ч. 2. – С. 198–201.

4. Медведев А.В. Концепция оптимизационно-имитационного моделирования регионального социально-экономического развития / А.В. Медведев // Международный журнал прикладных и фундаментальных исследований. – 2013. – № 7. – С. 21–25.

5. Моделирование производственно-инвестиционной деятельности фирмы / Под ред. Г.В. Виноградова. – М.: ЮНИТИ-ДАНА, 2002. – 319 с.

6. Победаш П.Н. Модели оптимального управления и операционного исчисления для многокритериального анализа экономических систем: монография / П.Н. Победаш, Е.С. Семенкин. – Красноярск: Сиб. федер. ун-т, 2012. – 260 с.

7. Программа для решения многошаговой задачи линейного программирования методом последовательных приближений («Линейная динамика») / Программа для ЭВМ. Свидетельство о регистрации в Роспатенте № 2004611491 от 17.06.2004. Правообладатели: А.В. Медведев, П.Н. Победаш. 2.Конструктор и решатель дискретных задач оптимального управления («Карма») / Программа для ЭВМ. Свидетельство о регистрации в Роспатенте № 2008614387 от 11.09.2008. Правообладатели: А.В. Медведев, П.Н. Победаш, А.В. Смольянинов, М.А. Горбунов.

Использование автоматизированных средств и систем поддержки принятия решений в бизнес-планировании являются важнейшими факторами успеха в бизнесе. Они позволяют предпринимателю, бизнесмену или экономисту-аналитику давать оперативную и обоснованную оценку стоимости и разрабатывать сценарии развития своего бизнеса, экономя, в первую очередь, драгоценное время при принятии инвестиционных, производственных и финансовых решений.

Принятие решений в сфере бизнес-планирования практически затруднено из-за многообразия и сложности требующих учета бизнес-процессов – инвестиционного, производственного, финансового, управленческого и пр., а также многочисленности характеристик внешнего и внутреннего рыночного окружения бизнес-проекта. Это ставит перед принимающим решения лицом (ЛПР) сложные задачи, эффективное решение которых невозможно без использования системного подхода, под реализацией которого в данном случае будем понимать наличие следующих инструментов:

– математических моделей, адекватно отражающих содержательную сторону бизнес-процессов;

– методов и алгоритмов анализа указанных математических моделей, допускающих автоматизированную обработку извлекаемой из них информации;

– программных комплексов, численно реализующих указанные методы и алгоритмы анализа и дающих возможность ЛПР обрабатывать и представлять полученную информацию в автоматизированном режиме.

Будем называть перечисленный комплекс средств системой поддержки принятия решений (СППР).

Первоочередной задачей в планировании бизнес-процессов является оценка их экономической эффективности. В большинстве современных работ в данной области для построения критериев эффективности используются агрегированные функционалы качества (производственные функции (ПФ), функции благосостояния, полезности, отражающие различные содержательные аспекты деятельности экономических агентов – максимизацию прибыли, выпуска продукции или конечного потребления, минимизацию производственных затрат и других показателей. Указанные функционалы качества, как правило, строятся на основе использования содержательно идеализированных математических зависимостей, которые, отражая в целом теоретические закономерности экономических теорий полезности, спроса и предложения, благосостояния, зачастую не устраивают экономистов-практиков, так как реальные зависимости значений функционалов качества от используемых экономических ресурсов (труд, капитал, финансы и пр.) на практике редко совпадают с зависимостями, описываемыми указанными функциями. Кроме того, такая идеализация:

– существенно ограничивает возможности учета информации микроэкономического уровня при расчете доходных и расходных составляющих бизнес-процессов;

– не позволяет использовать понятные для целевой аудитории алгоритмы обработки и представления информации бизнес-процессов;

– затрудняет разработку удобных для целевой аудитории автоматизированных программных средств поддержки принятия решений в управлении бизнес-процессами.

Пусть деятельность производителя продукции (товаров и/или услуг) описывается, выраженными в стоимостном виде, материальными и финансовыми потоками стратегического (прибыль, инвестиции) и тактического (выручка от продажи продукции, амортизация, фонд оплаты труда, налоги, оборотные затраты, кредиты, дотации и пр.) характера. Предположим, кроме того, что организационную деятельность производителя можно разделить на три составляющие [5]:

– инвестиционная (учет потоков, обусловленных функционированием основных производственных фондов (ОПФ),

– производственная (учет выручки, затрат на амортизацию ОПФ, оплату труда, сырья и материалов, энергии и т.п.)

– финансовая (учет кредитов, налогов, сборов, дотаций и других доходно-расходных финансовых потоков).

Алгоритм преобразования ресурсов (труд (L), капитал (K), финансы (Ф)) в экономический результат (прибыль, чистую приведенную стоимость и др.) называется производственной функцией (ПФ). Построение универсальной ПФ, понимаемой в смысле ее независимости от типа (производство товаров/услуг) или специфики (отрасль хозяйства, сфера приложений) производственной деятельности, является важной задачей при ее моделировании, так как дает возможность дать численную оценку эффективности и учесть максимально большое количество бизнес-процессов. В качестве ПФ, для простоты, часто используются различные идеализированные математические функции, например, линейные (Э(K, L) = αK + βL), иррациональные (Э(K, L) = γKαL1-α, 0 < α < 1) и даже трансцендентные (например, логистическая) функции. Однако, как было упомянуто выше, это зачастую не устраивает экономистов-практиков. В этой связи ниже приводится краткий алгоритм расчета ПФ, применимый в случае оценки эффективности производства как товаров, так и услуг, согласованный с принятыми в Российской Федерации основными бухгалтерскими правилами учета доходов и затрат, который получил поддержку экономистов-практиков и апробирован при решении многочисленных задач бизнес-планирования [1, 3].

Обозначим ОП(t) – объем производства, СС(t) – собственные средства производителя, ОС(t) – оценка остаточной стоимости имущества, Д(t) – оценка доходов, Р(t) – оценка расходов, И(t) – инвестиции, П(t) – чистая прибыль,. Тогда в предположении, например, что инвестиции тратятся только на капитальный ресурс (И = К), получим следующие выкладки:

Д = F(ОП), З = F1(К, ОП) + F2(L, ОП),

П = (Д – З)×

× (1–{ставка налога на прибыль}),

ОС = F3(К),

и производственную функцию можно выразить, например, в следующем виде:

Э(K, L) = d1*П + d2*ОС – d3*И,

где d1,d2,d3 – дисконтирующие множители, учитывающие общеэкономический закон обесценения финансовых потоков во времени;

Ключевое для реализации любого бизнес-проекта требование платежеспособности производителя можно описать неравенством СС ≥ 0, где СС = П + F4(Ф) – И.

Здесь функции F, F1, F2 описывают производственную деятельность, F3 – остаточную стоимость с учетом амортизационных затрат, F4 – финансовую деятельность.

Выделим далее, вообще говоря, аксиоматическое положение, что алгоритмы расчета показателей финансово-хозяйственной деятельности фирмы могут достаточно корректно, без существенной потери точности моделирования, описываться линейными функциями F, F1, F2, F3, F4.

Это положение, в частности, является важным аргументом для дальнейшей реализации системно-аналитической концепции моделирования, так как позволяет использовать хорошо разработанные методы и алгоритмы численного анализа линейных моделей оптимизации при практически значимых размерностях искомых переменных, определяемых количеством видов продукции и содержательных ограничений в моделируемых бизнес-процессах.

Исходя из указанного положения о линейности функций F, F1, F2, F3, F4, будем строить задачу бизнес-планирования в форме многокритериальной, многошаговой задачи линейного программирования (ММЗЛП) вида:

x(t + 1) = A(t)x(t) + B(t)u(t); x(t) = a;

C(t)x(t) + D(t)u(t) ≤ h(t); u(t) ≥ 0

(t = 0,…,T – 1); (1)

,

,

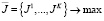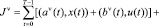
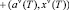где u(t) = [ul(t)] и x(t) = [xi(t)] – соответственно управляющий и фазовый векторы; матрицы A(t) = [aij(t)]; B(t) = [bil(t)]; C(t) = [ckj(t)]; D(t) = [dik(t)]; векторы a(t) = [ai(t)]; b(t) = [bl(t)]; s(t) = [si(t)]; h(t) = [hk(t)]; (i, j = 1,…,n; l = 1,…,r; k = 1,…,m; t = 0,…,T); Jν – ν-тый целевой критерий (ν = 1,…,K); K – количество критериев; r, m, T – размерность управляющего вектора, число ограничений и временных шагов соответственно; (α0,β0) – скалярное произведение векторов α0, β0; n – количество видов продукции.

В соответствии с основными учитываемыми бизнес-процессами, разделим фазовые и управляющие переменные, а также ограничения в (1) на инвестиционные, производственные и финансовые. В таблице отражена информация о взаимодействии ограничений и переменных в математических моделях экономических систем, многочисленные реализации которых описаны в работах [2, 6]. Тонированные клетки в таблице указывают, какие переменные задействуются в соответствующих ограничениях математических моделей.

Mатрица взаимодействия «ограничения-переменные»

Переменные в таблице имеют следующий содержательный смысл. УИ – инвестиции в текущий момент времени на приобретение комплекта основных производственных фондов (ОПФ), ФИ – накопленные инвестиции в ОПФ; УП – суммарная стоимость реализованной продукции в текущий момент времени, ФП – накопленные амортизационные отчисления, стоимость реализованной продукции; УФ и ФФ – стоимостное выражение (соответственно, в текущий момент и накопленных) потоков кредитов, депозитов, дотаций и других финансовых инструментов. Ограничения, описывающие функционирование производителя, имеют следующий содержательный смысл. Уравнения: динамика фазовых переменных ФИ, ФП, ФФ. Неравенства: ОИ – по суммарному объему инвестиций, ОП – по фондоотдаче ОПФ и по спросу на продукцию, ОФ – по суммарному стоимостному выражению объемов финансовых инструментов.

В работе [2], в частности, обоснована возможность математически корректного превращения задачи (1), путем применения к векторам x(t) и u(t) (доопределенным нулевыми компонентами на бесконечном горизонте планирования) z-оператора:

,

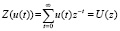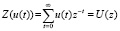(2)

в многокритериальную статическую, z-параметрическую задачу линейного программирования:

(k)c1×2n·X2n×1(z) → max,

AL×2n·X2n×1(z) ≤ bL×1, (k = 1,…, K) (3)

где L – количество ограничений (требования платежеспособности, ограниченность выручки спросом или фондоотдачей ОПФ, ресурсные ограничения и пр.), описывающих конкретный вид производственной деятельности, bL×1 – вектор-столбец правых частей ограничений, c1×2n – вектор-строка коэффициентов целевой функции, AL×2n – матрица коэффициентов ограничений. Отметим, что здесь z = 1 + r, где параметр r имеет естественный экономический смысл ставки дисконтирования инвестиционного проекта.

Отметим, что в задаче (3) принципиально сохраняется классификация переменных и ограничений таблицы, но модифицируется их структура (устраняется деление переменных на фазовые и управляющие), а также содержательная трактовка. А именно, инвестиционные переменные трактуются как суммарная стоимость ОПФ (суммарные инвестиции), а производственные переменные – как суммарная стоимость произведенной продукции на всем горизонте планирования. Кроме того, задача (3) сохраняет некоторые основные качественные свойства исходной динамической задачи (1): оптимальные пропорции инвестиций, выпусков продукции, структуру, параметрические зависимости Парето-множеств и т.п. [2]. Помимо указанного преимущества, применение операционного метода позволяет значительно упростить процедуру доказательства существования решения исходной динамической задачи. Полученная статическая задача допускает эффективный численный анализ и может быть решена для практически значимых размерностей, определяемых в экономических системах, прежде всего, количеством видов производимой продукции и учитываемых ограничений.

Использование указанных в таблице переменных, наряду с возможностью определения их оптимальных значений, позволяет:

● рассчитывать основные показатели финансово-хозяйственной деятельности фирмы: потоки прибыли, амортизации, оплаты труда, кредитов, штрафов, основные виды налогов и сборов и т.п.;

● описывать ограничения функционирования производителя, связанные с его производственными, инвестиционными и финансовыми возможностями: платежеспособность, ограниченность выпуска спросом на продукцию и возможностями ОПФ, кредитно-депозитные, страховые, дотационные и другие ограничения.

Описанный подход к моделированию процессов бизнес-планирования, в части использования математического класса задач, алгоритмов расчета доходных и расходных бизнес-потоков, классификации переменных, применения операционного метода и других элементов концепции, позволил построить и проанализировать многочисленные модели экономических систем (см. обзоры [3, 4]). При этом, с учетом линейности моделей (1), (3), возникает реальная возможность на практике разрабатывать пакеты программ для автоматизированного ввода-вывода и оптимизационного анализа информации об основных бизнес-процессах в формате, устраивающем конечного пользователя – экономиста-практика, финансового аналитика, предпринимателя.

Большинство используемых в настоящее время программных продуктов в сфере бизнес-планирования (ProjectExpert, Альт-инвест, ИНЭК-Аналитик и др.) базируются на имитационных моделях деятельности предприятий, аналитической основой которых выступают системы дифференциальных, разностных или алгебраических уравнений и неравенств, описывающих бизнес-потоки и ограничения их функционирования. Имитационные модели характеризуются высоким уровнем детализации материальных и финансовых потоков предприятия, однако, не решая задач оптимального управления, обладают следующими, существенными для бизнес-планирования, недостатками:

1) не предназначены для получения оптимальных значений показателей эффективности и, тем самым, оценки потенциала деятельности предприятий;

2) как правило, требуют большого количества численных реализаций параметров модели только для того, чтобы «нащупать» квазиоптимальные значения переменных и показателей эффективности, не гарантируя, вообще говоря, даже приближения к ним.

Напротив, использование оптимизационных моделей (1),(3), позволяет решать важные задачи в сфере экономического планирования и прогнозирования бизнес-процессов, не доступные при использования имитационных моделей, и, в первую очередь, задачи определения потенциалов бизнес-потоков. Модели (1),(3) легли в основу решателя программного комплекса [7], имеющего встроенные блоки занесения и контроля входной информации, графического, многопараметрического и многокритериального анализа. Основные результаты использования [7] приведены в обзорах [3, 4].

Описанный в данной работе подход успешно реализован при анализе бизнес-проектов как товарного производства (в том числе инновационного), так и производства услуг коммерческого характера. В настоящее время разработанная система поддержки принятия решений развивается в направлении конечного пользователя – предпринимателя, бизнес-аналитика, управленца регионального уровня – дополняясь блоками автоматизированной предобработки (автоматизированного внесения информации в пакет), а также постобработки полученной при решении информации.

Таким образом, полученный опыт реализации системного подхода к решению и анализу задач бизнес-планирования, включающий их математическое моделирование в форме ММЗЛП, теоретический и численный анализ, автоматизированную информационно-аналитическую систему на основе программного комплекса [7], дает основание говорить о практической реализации комплексной оптимизационной системы поддержки принятия решений в бизнес-планировании.

Библиографическая ссылка