В процессе движения механизмов переменной структуры (МПС) изменяются числа подвижных звеньев, степени свободы, виды и классы механизма. Это позволяет использовать их в качестве манипуляционных устройств для выполнения сложных технологических процессов и механизмов ударного действия. Отрицательной стороной МПС является появление дополнительных ударных нагрузок в момент изменения структуры механизма [1].
Математической моделью механизма переменной структуры является дифференциальное уравнение с разрывными коэффициентами, в частности, приведенный момент инерции является кусочно-непрерывной и положительно определенной функцией положения. В работах Джолдасбекова У.А., Уалиева Г.У., Антонюка Е.М., Абдраимова С., Ярунова М. и др. рассмотрены некоторые задачи структуры, кинематики и динамики кулачково-рычажных механизмов переменной структуры, применяемые в горнодобывающей и текстильной промышленности. В этих механизмах структура меняется за счет упругих звеньев и связей, наличием выстоя некоторых звеньев шарнирно-стержневых механизмов различных классов. Определение законов движения таких механизмов связано с решением дифференциальных уравнений движения с конечно-разрывными коэффициентами. В основном, в многозвенных механизмах переменной структуры правая часть уравнения – обобщенная сила – представляет непрерывную функцию положения и времени. Задача заключается в определении закона движения звена приведения механизма переменной структуры в окрестности точки разрыва инерционных параметров. Предлагаем новую методику определения закона движения звена приведения механизмов переменной структуры с нелинейными функциями положения с одной степенью свободы, движение которого описывается уравнением
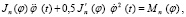 (1)
(1)
Допустим, что в положении φ = φk механизм меняет структуру, т.е. φk – является координатой точки разрыва функции Jn(φ). Производная J’n(φ) понимается в обобщенном смысле [2]. Поэтому, обобщенная функция, соответствующая функции J’n(φ), имеет вид
J’n(φ) = ΔJδ(φ – φk),
где ΔJ – конечный разрыв приведенного момента инерции,
δ(φ – φk) – функция Дирака.
Теперь уравнение (1) записывается в виде:
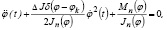 (2)
(2)
В данной работе сделана попытка распространения метода переменного масштаба времени [2] для данного дифференциального уравнения второго порядка.
Введем замену
y(φ) = U(z),
где z = ψ(t)
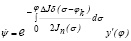 ,(2’)
,(2’)
Тогда нелинейное уравнение движения преобразуется в линейное
U’’(z) + U(z) = 0 (3)
Допустим, что U(z) и ψ(z) дважды непрерывно дифференцируемые функции, тогда имеем
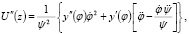 (4)
(4)
Подставив выражение (4) в уравнение (3), имеем
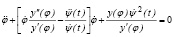 (5)
(5)
Сравнивая уравнения (5) и (2), получим
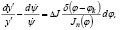 (6)
(6)
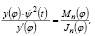 (7)
(7)
Интегрируя выражения (6) и полагая, что постоянная интегрированная равна нулю, получим
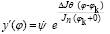 ,
,
где
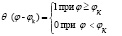
функция Хевисайда.
Подставив
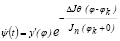 (8)
(8)
в уравнение (7), имеем
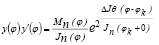
Интегрируя уравнение (8) и предположив, что y(0) = 0, получим
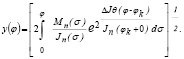 (9)
(9)
Как известно, решение уравнения (3) имеет вид
y(φ) = c1cos ψ(t) + c2sin ψ(t) (10)
Покажем, что (10) удовлетворяет уравнение (2).
Действительно, из (10) получим
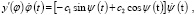
Отсюда, учитывая (8), имеем
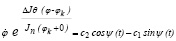
Продифференцируя это выражение по t [3], получим
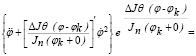
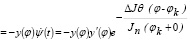
или
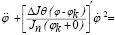
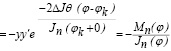 .
.
Найдем теперь обобщенную производную
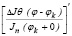 .
.
По свойству обобщенной функции имеем
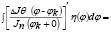
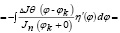
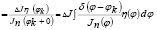
Следовательно,
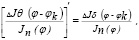
Отсюда приходим к уравнению (2)
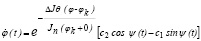 ,
,
здесь ψ(t) определяется из уравнения (2’), а y(φ) из уравнений (9).
Произвольные постоянные определяются из начальных условий (11): 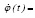
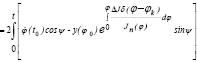 dt
dt
где
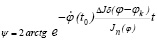
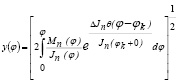
Таким образом, в положении, когда механизм меняет свою структуру, т.е. в окрестности точки разрыва инерционных характеристик [4], угловую скорость звена приведения можно вычислить по выражению (11).
Библиографическая ссылка
Уалиев З.Г., Уалиев Г., Уалиева И.М. ДИНАМИЧЕСКИЙ АНАЛИЗ МЕХАНИЧЕСКИХ СИСТЕМ ПЕРЕМЕННОЙ СТРУКТУРЫ // Успехи современного естествознания. 2015. № 1-8. С. 1361-1363;URL: https://natural-sciences.ru/ru/article/view?id=35403 (дата обращения: 16.02.2026).



