Несмотря на многочисленные работы по дегидроксилации минералов, детального понимания и теоретического анализа процесса дегидроксилации до сих пор нет [2, 3, 5–13].
Ранее нами в статье [14] с позиций квантовой механики рассмотрен механизм дегидроксилации минералов. Процесс дегидроксилации представлен как процесс локализации протона в системе «два атома кислорода и протон между ними». Такое перемещение протона обусловлено его переходом в возбуждённое состояние. При нагреве в минерале происходит увеличение энергии протона, в связи с этим растёт прозрачность среднего барьера.
Недостаточно изучен вопрос об изменении интенсивности полосы валентных колебаний ОН. Таким образом, существует необходимость поиска ряда количественных характеристик в системе ОН…О.
Была выбрана модель из двух источников с параболической зависимостью потенциальной энергии U. Две потенциальные зависимости (U1 и U2), характеризуют воздействие двух рассматриваемых атомов на протон, при этом учтено смещение минимумов потенциальных энергий данных источников на величину ΔU = U2 min – U1 min. Определена координата промежуточного барьера, разделяющего потенциальные ямы, его высота.
Локализация протона, связанного с одним из атомов кислорода, определяется его волновой функцией. Поведение микрочастицы соразмерно волновому уравнению Шрёдингера, полностью определяющего её движение.
Вероятность локализации частицы в пространстве определяется её волновой функцией, а квадрат её модуля даёт значение плотности вероятности нахождения частицы в данной области.
Вероятность обнаружения микрочастицы вблизи второго атома кислорода мала. Однако, наличие второго потенциального барьера, меняет данную вероятность. Также понятно, что при увеличении энергии протона (т.е. при его переходе в возбуждённое состояние) растёт прозрачность среднего барьера вследствие туннельного эффекта. Изменение вероятности нахождения протона вблизи второго потенциального источника соответствует процессу дегидроксилации рассматриваемой системы.
Общая потенциальная энергия системы двух близко расположенных осцилляторов U(x) имеет промежуточный барьер ΔU с координатой
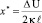. (1)
Выражение (1) соответствует пересечению потенциальных функций гармонических осцилляторов U1 (x) и U2 (x), имеющих вид:
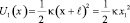, (2)
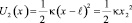. (3)
Высота промежуточного барьера, разделяющего потенциальные ямы, определяется выражением:
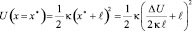(4)
или
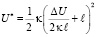. (5)
Локализация протона, связаная с одним из атомов кислорода, определяется его волновой функцией ψ(x).
Для первого изолированного атома с потенциальной энергией U1 (x) запишем:
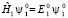. (6)
Здесь волновая функция ψ является решением стационарного уравнения Шрёдингера, для второго атома
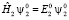. (7)
Функци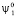и 
и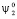 
– волновые функции, которые соответствуют двум близко расположенным изолированным потенциальным источникам с невозмущёнными энергетическими уровнями.
Отказавшись от описания движения частицы с помощью траекторий, получаемых из законов динамики, и определив вместо этого волновую функцию, необходимо ввести в рассмотрение уравнение, эквивалентное законам Ньютона и дающее рецепт для нахождения ψ в частных физических задачах. Таким уравнением является уравнение Шрёдингера [6, 7]:
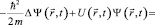
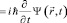(8)
или
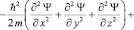
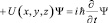. (9)
В квантовой механике вводят оператор Гамильтона –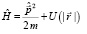 
квантово-механический оператор, соответствующий функции Гамильтона в классической механике:
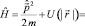
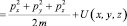. (10)
В представлении Шрёдингера эволюция системы описывается зависимостью от времени вектора состояния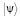 
системы [1, 4]:
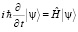. (11)
Если классическая функция Гамильтона не зависит явно от времени, то она является интегралом движения и значение её совпадает с энергией системы. Соответственно гамильтониан системы в этом случае является оператором энергии. Уравнение (11) при этом имеет частные решения в виде стационарных состояни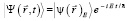й 
или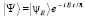 
. Вектор состояния 
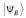не зависит от времени и является собственным вектором гамильтониана 
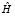, соответствующим значению энергии E:
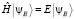. (12)
Данное уравнение определяет спектр энергии системы.
Для нашей задачи гамильтониан имеет вид:
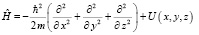
или
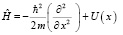. (13).
С учётом (2) и (3) перепишем (13) в виде:
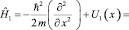
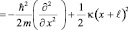. (14)
и
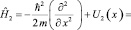
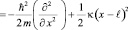. (15)
Функция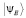 
определяет квантовое состояние и должна быть однозначна, конечна и непрерывна. В системе, занимающей реальный объём, решение имеется не для любых значений энергии. Допустимые значения энергии Ei являются дискретными величинами, при этом набор этих значений (собственные значения оператора Гамильтона) образует энергетический спектр.
При сближении двух источников их волновые функции и энергетический спектр взаимно нарушаются. Важной задачей при этом является нахождение новых энергетических уровней и возмущённых волновых функций, характеризующих взаимодействие рассматриваемых объектов. Результирующая волновая функция ψ исследуемой системы в соответствии с законами квантовой механики может быть найдена как линейная комбинация невозмущённых волновых функци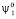й 
и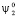 
изолированных друг от друга источников:
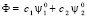. (16)
Уравнение (12) примет вид:
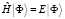. (17)
Энергетический спектр такой системы определяется соответственно стандартным выражением:
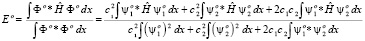. (18)
После ввода упрощающих обозначений
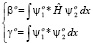(19)
получим:
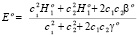. (20)
Используя метод вторичного квантования [1], основанный на том, что состояния микрочастиц характеризуют набором чисел – числами заполнения, определим искомые величины. При этом вместо волновых функций частиц в координатном представлении вводятся волновые функции в представлении чисел заполнения различных состояний одной частицы. Удобство метода вторичного квантования в том, что он позволяет единообразно описывать системы с различным числом частиц, как с конечным фиксированным (в задачах физики конденсированных сред), так и с переменным. Переходы между различными состояниями (например, из состояния k в состояние q одной частицы при этом описываются как уменьшение числа заполнения, соответствующего одной волновой функции на единицу (Nk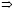 
Nk – 1), и увеличение числа заполнения другого состояния на единицу (Nq 
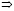Nq + 1). Вероятности этих процессов зависят не только от элементарной вероятности перехода, но и от чисел заполнения участвующих в процессе состояний.
С учётом (6) и (7) и (14) и (15) решим уравнение второго порядка (20), определив соответствующие коэффициенты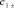 
и 
:
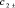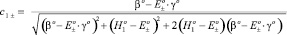(21)
и
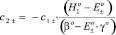. (22)
Также можно рассчитать новые значения энергии волновой функции и для возбуждённых уровней. В основном и первом возбуждённом состояниях выражения волновых функций протона и значений его энергий имеют вид для n = 0 и n = 1 соответственно:
, 
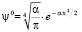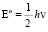(23)
и
, 
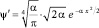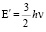, (24)
где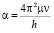 
и ν – частота, μ – приведённая масса осциллятора.
Из (2), (3) и (23) получим в рассматриваемом случае:
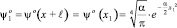(25)
и
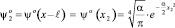. (26)
Для волновых функций, соответствующих возбуждённым состояниям, запишем с учётом выражения (24):
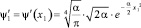(25)
и
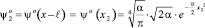. (26)
Также определяются и другие параметры задачи: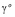 
, 
, 
, 
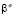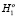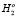и соответственно γ’, β’ и 
, 
.
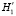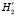Введём параметр η, определяемый следующим равенством:
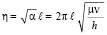. (27)
Здесь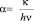 
, так как частота осциллятора и его приведённая масса μ связаны соотношением:
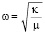. (28)
В результате расчётов получим уравнения, связывающие частоту ν изолированного источника с безразмерным параметром η, задаваемым выражениями (28) и (29) и характеризующим ширину потенциального барьера.
Из (1)–(3) получим:
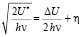(29)
или
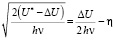. (30)
Уравнения (21) и (22) позволяют определить степень локализации протона вблизи соответствующих атомов кислорода, вычисляя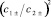 
– отношение квадратов коэффициентов общей волновой функции системы.
Задавая различные значения ?U и η, можно найти положение энергетических уровней и степень их локализации.
Последующий анализ зависимости интенсивности полос поглощения в рассматриваемых системах, с учётом полученных формул, приводит к выводу о том, что интенсивность полос ОН уменьшается с ростом температуры. В рамках модели, в которой протон гидроксильной группы находится в «двойной потенциальной яме», удовлетворительно объясняется уменьшение интенсивности полос поглощения гидроксилов при повышении температуры.
Таким образом, предложенная модель позволяет выявить основные черты механизма дегидроксилации в минералах.
Библиографическая ссылка
Шишелова Т.И., Липовченко Е.Л. КВАНТОВО-МЕХАНИЧЕСКИЙ РАСЧЁТ ДЕГИДРОКСИЛАЦИИ МИНЕРАЛОВ // Успехи современного естествознания. – 2015. – № 12. – С. 177-181;URL: https://natural-sciences.ru/ru/article/view?id=35770 (дата обращения: 20.04.2024).