Зеленые насаждения являются неотъемлемой составляющей не только природных, но и городских экосистем и выполняют весьма важные экологические функции: cредообразующие; санитарно-гигиенические; рекреационные; эстетические.
В озеленении г. Красноярска достаточно широко на протяжении нескольких десятилетий используется тополь бальзамический (Populus balsamifera). Деревья этого вида распространены во всех районах города, в парках, во дворах, вдоль автомобильных дорог. Встречаются как чисто тополиные посадки, так и в смешении с другими древесно-кустарниковыми растениями. В связи с большим количеством пуха, который является бичом города в летнее время, со старением деревьев, их интенсивным ростом в городе производится массовая обрезка деревьев [1, 2]. Тополь достаточно часто используется как вид-индикатор для оценки здоровья среды города, но в работах не указывается, для обрезанных или необрезанных деревьев рассчитывается интегральный показатель флуктуирующей асимметрии (ФА) [3]. Так как в г. Красноярске присутствует большое количество тополей, подвергшихся обрезке, было интересно оценить стабильность их развития, используя метод флуктуирующей асимметрии.
Цель исследования
Оценить жизненное состояние в городской среде тополя бальзамического (Populus balsamifera), подвергавшегося обрезке.
Материалы и методы исследования
В качестве пробной площади был выбран остров Татышев, расположенный на реке Енисей в черте г. Красноярска. Его протяжённость составляет около 6 км вдоль течения реки и 1,5 км поперек. На острове присутствует большое количество обрезанных и необрезанных тополей, произрастающих в одинаковых условиях, что позволяет провести сравнительный анализ стабильности их развития. Для исследования была взята центральная часть острова.
Предварительная, визуальная оценка жизненного состояния бальзамических тополей с обрезанной и необрезанной кроной проводилась с помощью шкалы категорий состояния деревьев, приведенной в Санитарных правилах в лесах РФ (2011 г.) [4].
Для оценки взаимосвязи состояния деревьев с их морфометрическими показателями использовали метод флуктуирующей асимметрии. Было исследовано 30 случайно выбранных одновозрастных деревьев, подвергшихся обрезке 3 года назад. С каждого дерева было собрано по 10 листьев, пригодных для анализа, на высоте 180–200 см. Листья собирались по кругу. Так же определение ФА было проведено для 30 необрезанных деревьев.
Для каждого листа определяли по пять билатеральных признаков: 1 – ширина половины листа; 2 – длина второй жилки; 3 – расстояние между первой и второй жилкой в центральной части листа; 4 – расстояние между первой и второй жилкой на периферии листа; 5 – угол между главной и второй жилкой. Измерения проводились в период, когда завершается интенсивный рост листьев [5].
Флуктуирующая асимметрия (ФА) рассчитывалась по формуле
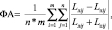 (1)
(1)
где Lлij и Lпij соответственно левый и правый признак – j, исследуемого объекта – i.
Для оценки характера асимметрии используемых метрических билатеральных признаков, использовали статистические методы анализа. Для определения характера распределения признаков и их разности использовались критерии Колмогорова – Смирнова (К-С), описательная статистика, графические методы. Для выявления направленной асимметрии использовали F-тест и двухвыборочный t тест с одинаковыми дисперсиями для величин признаков с правой и левой стороны листа.
Обработка результатов проводилась при помощи пакета анализа «Статистика Version10».
Результаты исследования и их обсуждение
Визуальная оценка жизненного состояния бальзамических тополей показала, что 27 из 30 обрезанных тополей (90 %) не имеют видимых признаков ослабления, а оставшиеся 3 дерева (10 %) можно отнести к ослабленным. Из 30 тополей, не подвергавшихся обрезке, 25 (83,3 %) не имеют видимых признаков ослабления, а (16,7 %) можно отнести к ослабленным.
Элементом феногенетической изменчивости, например, тополя, является флуктуирующая асимметрия (ФА) листовой пластины. Основными критериями ФА являются ее независимость и случайность, поэтому она не должна иметь четко выраженной направленности. Другими словами одна половинка листа должна изменяться независимо от второй. В связи с этим необходимо выявить характер асимметрии, то есть исключить такие ее виды, как направленная асимметрия (НА) и антисимметрия (АС), для этого необходимо оценить характер распределения, используемых билатеральных признаков и отсутствие достоверных различий между их значениями справа и слева.
Для исключения АС необходимо оценить нормальность распределения, используемых признаков. Проверку распределения используемых билатеральных признаков проводили, используя К-С при D > 0,08 и p < 0,05 распределение отличается от нормального. При идеальном нормальном распределении величины асимметрии и эксцесса должны равняться 0, а значение медианы (Ме) и среднего совпадать. В нашем случае распределение можно отнести к нормальному, если величина асимметрии (А) не превышает 0,25, а эксцесса (Е) – 2,59 (для выборки объемом n = 300 и уровня значимости p = 0,05).
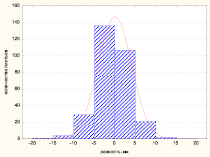
Характер распределения значений ширины листовой пластины слева и справа и их разности для обрезанных тополей представлен на рис. 1.
Характер распределения для значений левой, правой половины практически одинаков (рис. 1, а). По величине критерия К-С D = 0,0.064, p < 0,2. Для ширины листовой пластины слева значения А = –0,17, Е = 0,11, среднее значение признака Xср,л = (62,9 ± 0,40) мм, медиана Ме = 64 мм; для распределения ширины листовой пластинки справа – А = –0,21, Е = 0,40, Xср,пр = (62,9 ± 0,39) мм, Ме = 64 мм. Таким образом, распределение значений ширины листовой пластины слева и справа можно считать нормальным островершинным с незначительной левой асимметрией. Распределение разности между шириной листовой пластины слева и справа (рис. 1, б) подтверждает флуктуирующий характер изменения признака, так как также подчиняется нормальному значению, со средним значением Xср = (0 ± 0,11) мм, Ме = 0 (А = –0,04, Е = 1,1, D = 0,07, p < 0,11 ).
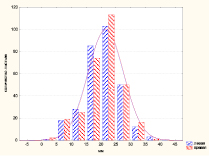
Распределение значений второго признака – длина второй жилки и ее разности с левой и правой сторон листовой пластины для обрезанных тополей представлено на рис. 2.
Для длины второй жилки листьев значения слева А = –0,17, Е = 1,05, К-С D = 0,077, p < 0,11; справа – А = –0,14, Е = 1,35; К-С D = 0,078; p < 0,1, то есть оба распределения данного признака также можно отнести к нормальному закону распределения. Среднее значение длины второй жилки с правой стороны листовой пластинки Xср,пр = (74,3 ± 0,40) мм, Ме = 75, для левой – Xср,л = (74,2 ± 0,43) мм, Ме = 75. Распределение разности длины второй жилки листьев слева и справа (рис. 1, б) подтверждает флуктуирующий характер изменения признака, так как подчиняется нормальному значению, со средним значением близким к 0 Xср = (0,08 ± 0,23) мм, Ме = 0 (А = –0,10, Е = 0,66, D = 0,072, p < 0,10).
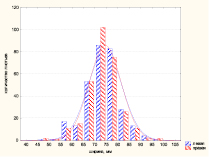
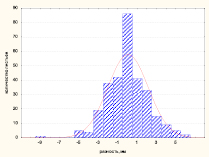
а) б)
Рис. 1. Распределение значений ширины листовой пластины (а) и разности между шириной слева и справа (б)
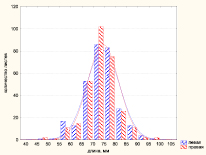
а) б)
Рис. 2. Распределение значений длины второй жилки листовой пластины (а), и значений ее разности слева и справа (б)
а) б)
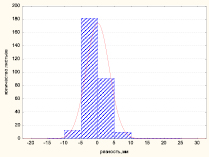
Рис. 3. Распределение значений расстояния между первой и второй жилкой в центральной части листа (а) и их разности (б)
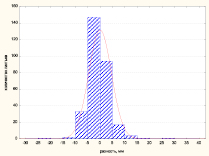
а) б)
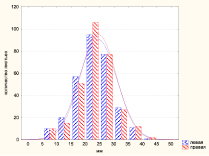
Рис. 4. Распределение значений четвертого признака – расстояние между первой и второй жилкой на периферии листа (а) и разности слева и справа (б)
Распределение значений третьего признака – расстояние между первой и второй жилкой в центральной части листа и разницей ее значений представлено на рис. 3.
Для расстояний между первой и второй жилкой в центральной части листа значения слева А = –0,23, Е = 0,62, К-С D = 0,0697, p < 0,15; справа – А = –0,40, Е = 0,42, К-С D = 0,076; p < 0,11; данный признак так же, как и предыдущие, можно считать нормально распределенным. Среднее значение расстояний между первой и второй жилкой в центральной части листа с правой стороны листовой пластинки Xср,пр = (21,6 ± 0,33) мм, Ме = 22 с левой – Xср,л = (21,6,2 ± 0,34) мм, Ме = 22. Распределение разности между первой и второй жилкой в центральной части листа с левой и правой стороны листа (рис. 1, б), подтверждает флуктуирующий характер изменения признака, так как подчиняется нормальному значению, со средним значением Xср = (0,10 ± 0,19,) мм, Ме = 0 мм (А = –0,25, Е = 2,06, D = 0,077, p < 0,10).
Распределение значений четвертого признака – расстояние между первой и второй жилкой на периферии листа и разности значений слева и справа для тополей, подвергавшихся обрезке, представлены на рис. 4.
По величинам асимметрии и абсцесса распределение четвертого признака наиболее близко к нормальному по сравнению со всеми ранее проанализированными признаками. Для значений признака слева А = 0,03, Е = 0,06, К-С D = 0,06, p < 0,15; справа А = 0,008, Е = 0,52, К-С D = 0,0697, p < 0,15. При этом можно отметить, что для значений признака слева и справа характерно повышенное рассеивание больших переменных, то есть в данном распределении присутствует незначительная правая асимметрия. Среднее значение расстояний между первой и второй жилкой на периферии листа с правой стороны листовой пластинки Xср,пр = (24,4 ± 0,36) мм, Ме = 25 мм, с левой – Xср,л = (24,2 ± 0,38) мм, Ме = 24 мм, а сами распределения соответствуют нормальному закону. Распределение разности между первой и второй жилкой на периферии листа с левой и правой стороны листа (рис. 1, б), также подчиняется нормальному распределению со средним значением Xср = (0,16 ± 0,03) мм и Ме = 0 (А = –0,26, Е = 2,75, D = 0,076, p < 0,10).
Распределение значений пятого признака – угол между главной и второй жилкой и разности его значений слева и справа для обрезанных тополей приведено на рис. 5.
Для распределении значений угла между главной и второй жилкой листовой пластинки значения показателей распределения равны слева А = –0,21 Е = –0,99, К-С D = 0,080, p < 0,05; справа – А = –0,26, Е = –0,14, К-С D = 0,087, p < 0,05. Среднее значение угла между главной и второй жилкой с правой стороны листовой пластинки Xср,пр = (59,8 ± 0,23)0, Ме = 600 с левой – Xср,л = (59,8 ± 0,32)0, Ме = 600. По критерию согласия К-С оба распределения данного признака нельзя отнести к нормальному закону распределения, при этом по величине эксцесса, асимметрии, равенстве моды, медианы и среднего значения распределение можно считать нормальным. Распределение разности значений угла слева и справа (рис. 1, б) подчиняется нормальному, со средним значением Xср = (0,02 ± 0,03)0, Ме = 00 (А = 0,26, Е = 2,7, D = 0,076, p < 0,10).
Проведенный анализ показал, что для четырех исследуемых признаков можно исключить антисимметрию, на основании статистических критериев К-С, значений асимметрии, эксцесса и совпадения средних значений с медианами распределений. Для всех признаков с левой и правой стороны листовой пластины наблюдается слабая левая асимметрия и островершинное нормальное распределение. Исключением является пятый признак – угол между главной и второй жилкой, распределение величин которого можно отнести к нормальному с определенными допущениями. Распределение разности значений всех признаков с левой и правой стороны листа подтверждает флуктуирующий характер их изменения.
Для выявления наличия или отсутствия направленной асимметрии использовали F-тест на равенство дисперсий двух выборок величин признака с правой и левой стороны листа. Результаты проведенного анализа представлены в таблице.
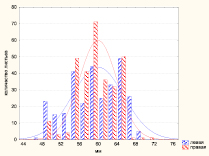
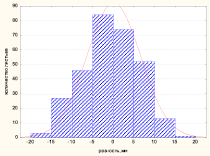
а) б)
Рис. 5. Распределение значений пятого признака – угол между главной и второй жилкой (а) и разность значений слева и справа (б)
Результаты F-теста и t теста на равенство дисперсий двух выборок величин признака с правой и левой стороны листа при уровне значимости p < 0,05
|
Признак |
Fст |
Fкр |
p |
tст |
tкр |
tкр-одностороннее |
|
ширина половины листа |
1,01 |
1,21 |
0,20 |
0 |
1,96 |
0,5 |
|
длина второй жилки |
1,12 |
1,21 |
0,15 |
0,14 |
1,96 |
0,44 |
|
расстояние между первой и второй жилкой в центральной части листа |
1,02 |
1,21 |
0,42 |
0,21 |
1,96 |
0,42 |
|
расстояние между первой и второй жилкой на периферии листа |
1,09 |
1,21 |
0,21 |
0,3 |
1,96 |
0,39 |
|
угол между главной и второй жилкой |
1,86 |
1,21 |
4,1*10-8 |
0,05 |
1,96 |
0,49 |
Для четырех метрических билатеральных признаков: ширина половины листа; длина второй жилки; расстояние между первой и второй жилкой в центральной части листа; расстояние между первой и второй жилкой на периферии листа; значение критерия Фишера, найденное экспериментальным путем Fст меньше критического значения Fкр при уровне значимости p < 0,05 (таблица). То есть отклонения с правой и левой стороны листовой пластины для каждого признака относятся к одной выборочной совокупности, то же самое подтверждает и двухвыборочный t-тест с одинаковыми дисперсиями. Для выборочных совокупностей значений угла между главной и второй жилкой с левой и правой части листовой пластины значение Fкр меньше критерия Фишера, найденного экспериментальным путем при уровне значимости p < 0,05 (таблица), то есть нельзя говорить о равенстве дисперсий двух совокупностей. В связи с этим использовали двухвыборочный t-тест с одинаковыми дисперсиями, который позволил подтвердить случайный характер изменений значений угла между главной и второй жилкой с левой и правой стороны листовой пластины, так как tкр-одностороннее < tкр (таблица). Проведенный статистический анализ метрических билатеральных признаков позволил исключить наличие НА для листьев тополя бальзамического (Populus balsamifera), подвергавшегося обрезке.
Заключение
Исследование пяти билатеральных признаков листьев тополей подвергшихся обрезке позволило для четырех из них исключить направленную асимметрию (НА) и антисимметрию (АС) и подтвердить флуктуирующий характер их вариаций. Из расчетов был исключен пятый признак – угол между главной и второй жилкой, так как его распределение отличается от нормального.
Рассчитанный средний интегральный показатель флуктуирующей асимметрии листьев 30 тополей, не подвергшихся обрезке ФАнеобр = (0,0373 ± 0,002), что соответствует 1 баллу шкалы оценки состояния видов-индикаторов по величине отклонений от симметрии. Для 30 тополей, подвергавшихся обрезке, ФАоб = (0,038 ± 0,002) тоже соответствует 1 баллу по этой шкале (ФА < 0,055) [5, 6] и позволяет оценить состояние тополей произрастающих на острове Татышев как условно нормальное, что так же подтверждает их визуальная оценка. Достоверных различий между полученными значениями, интегрального показателя для деревьев, подвергавшихся и не подвергавшихся обрезке, нет. Таким образом, обрезка тополей не отразилась на стабильности их развития, и обрезанные тополя можно использовать в качестве вида – индикатора здоровья окружающей среды.
Исследование выполнено при финансовой поддержке гранта РГНФ № 16-12-24023 «Методология моделирования и прогнозирования сценариев развития «зеленой экономики» и биоэкономики регионов в условиях активного хозяйственного освоения ресурсов Арктической зоны».
Библиографическая ссылка
Попельницкая И.М., Попов А.О. ФЛУКТУИРУЮЩАЯ АСИММЕТРИЯ ЛИСТЬЕВ ТОПОЛЯ БАЛЬЗАМИЧЕСКОГО (POPULUS BALSAMIFERA L.) В ГОРОДСКОЙ СРЕДЕ // Успехи современного естествознания. 2017. № 12. С. 72-78;URL: https://natural-sciences.ru/ru/article/view?id=36608 (дата обращения: 19.10.2025).
DOI: https://doi.org/10.17513/use.36608



