В горно-разведывательной отрасли не всегда удается применять традиционные методы для выявления местонахождения магнитных горных руд в силу удаленности объектов исследования, сложности и экономической дороговизны, неоднородности состава и т.д. [1; 2]. Поэтому к настоящему времени в Карачаево-Черкесской Республике (КЧР) не исследованы магнитные горные породы.
Для магнитных горных пород как предмета исследований условия образования в них различных намагниченностей являются весьма специфичными.
Наряду с этим следует учитывать также «немагнитные» внешние воздействия, оказывающие решающее влияние на приобретение различных видов намагниченностей.
Все это вместе приводит к возникновению особых видов намагниченностей, отличных от идеальной.
Целью данной работы является получение периодических электромагнитных полей, для того чтобы выявить местонахождение полезных ископаемых, в частности магнитных руд (КЧР).
Материалы и методы исследования
Для достижения данной цели разложили периодическую функцию в ряд Фурье, члены которого представляют собой гармонические колебания с частотами, кратными основной, и с амплитудами и фазами, различными для каждого члена и зависящими от характера разлагаемой функции.
Далее, используя теорему о наложении полей, рассмотрели каждую гармоническую составляющую в отдельности в зависимости величины М от времени:
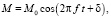 (1)
(1)
где f – частота колебаний;
δ – начальная фаза.
Решение задачи заключается в нахождении M0 и δ как функций координат в комплексном виде:
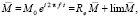 (2)
(2)
где 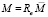 или
или 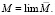
Тогда уравнения для переменного поля являются линейными и однородными:
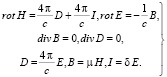 (3)
(3)
Величину 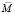 в уравнении (2) использовали в виде:
в уравнении (2) использовали в виде:
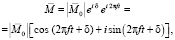 (4)
(4)
где 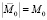 – вещественная часть.
– вещественная часть.
Полученную формулу (4) подставляли в систему уравнений (3), отделяя вещественную часть от мнимой, а также учитывая комплексные величины и дифференцируя по t, получили:
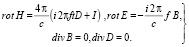 (5)
(5)
И на основании (4) имеем:
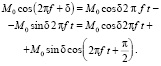 (6)
(6)
Формула (6) является суммой двух колебаний, одного с нулевой фазой и амплитудой, равной вещественной части 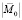 , и другого – отличающегося от первого по фазе
, и другого – отличающегося от первого по фазе 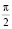 и с амплитудой, равной мнимой части M0.
и с амплитудой, равной мнимой части M0.
Далее рассмотрели, как меняется величина и направление вектора М, имеющего составляющие:
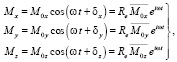 (7)
(7)
где 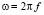 – круговая частота;
– круговая частота;
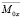 ,
, 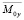 ,
, 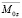 – комплексные амплитуды.
– комплексные амплитуды.
Результаты исследования и их обсуждение
Разлагая 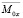 ,
, 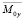 ,
, 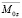 на вещественные и мнимые части, получили:
на вещественные и мнимые части, получили:
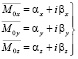 (8)
(8)
или
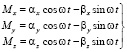 , (9)
, (9)
где
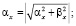
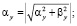
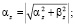
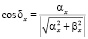 ;
;
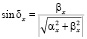 .
.
Из последних формул следует, что
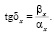 (10)
(10)
Обозначая
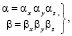 (11)
(11)
и на основании формулы (9) можно переменный вектор М рассмотреть как сумму двух векторов:
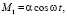 (12)
(12)
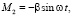 (13)
(13)
где M1 и M2 представляют собой линейные колебания с одинаковой частотой, но с разностью фаз 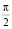 .
.
Известно, что два линейных колебания разных направлений, фаз и амплитуд, но одинаковой частоты при сложении дают эллиптическое колебание. Единичный вектор нормали этой плоскости равен:
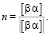 (14)
(14)
Если в формуле (14) α = 0 и β = 0 мы имеем неопределенность, если α ⃦ β, то имеем линейное колебание.
Квадрат векторов М из (9) равно:
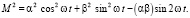 (15)
(15)
Учитывая в формуле (15), что
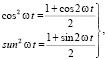 (16)
(16)
получили:
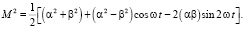 (17)
(17)
Далее, приравнивая 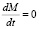 , получили:
, получили:
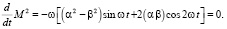 (18)
(18)
Если α2 = β2 и (αβ) = 0 одновременно, то имеем круговые колебания, как результат сложения двух взаимно перпендикулярных колебаний с одинаковыми амплитудами и с разностью фаз 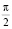 . Во всех остальных случаях уравнение (18) имеет определенное решение [3]:
. Во всех остальных случаях уравнение (18) имеет определенное решение [3]:
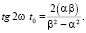 (19)
(19)
Необходимым условием максимума является:
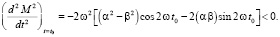 (20)
(20)
Из формулы (20) определяли:
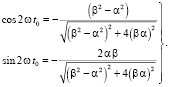 (21)
(21)
Тогда получим для 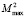 выражение:
выражение:
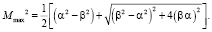 (22)
(22)
Обозначая величину большой полуоси через m, получили:
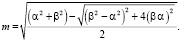 (23)
(23)
А малую полуось, обозначая через m' и учитывая, что 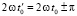 , получили:
, получили:
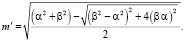 (24)
(24)
Для удобства вычисления допустили:
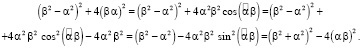 (25)
(25)
Аналогично можно вычислить и другие элементы, определяющие пространственные колебания.
Таким образом, определив αx, βx, αy, βy в плоскости XY, получили колебания с составляющими:
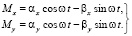 (26)
(26)
Тогда:
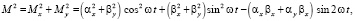 (27)
(27)
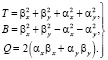 (28)
(28)
С учетом последней формулы выражение (27) принимает вид:
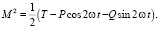 (29)
(29)
Условие максимума для выражения (29) имеет вид:
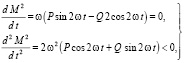 (30)
(30)
Первое условие дает нам:
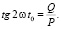 (31)
(31)
А второе показывает, что для максимума взяли решение соответствующее:
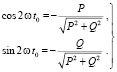 (32)
(32)
Подставляя формулы (32) и (31) в (29), получили:
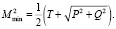 (33)
(33)
Выражение (33) есть фаза для составляющей большой оси:
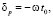 (34)
(34)
а фаза для малой оси соответственно равна:
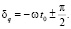 (35)
(35)
Причем если вектор обходит эллипс против часовой стрелки, то по оси z имеет знак (+), а в противоположном направлении соответственно знак (–) [4].
Измеряя электромагнитные величины, можно вычислить поле по формуле (9) во всех измеренных точках в любой момент времени [5–6].
Исследования показали, что одна и та же среда по отношению к полям различной частоты характеризуется различными параметрами, являющимися функциями частоты. А присутствие нескольких частот дает наложение полей, поэтому мы пользовались фильтрами частот.
Полученную математическую модель мы использовали на практике для выявления новых месторождений полезных ископаемых на природных объектах КЧР, методом электрического зондирования.
В избранном регионе устанавливали: автокомпенсатор электроразведки (АЭ-72), батарею, две катушки с проводом для разноса питающих электродов, и на расстоянии 2 м друг от друга заземляли два приемных провода (МN). А вдоль линии (MN) заземляли питающие электроды (АВ) на расстоянии 3 м от центра и измеряли величину тока в питающей линии и напряжения на питающих приемных электродах (рис. 1).
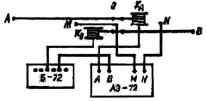
Рис. 1. Схема установки электрического зондирования
И по формуле:
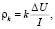
где 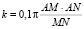 – коэффициент установки, определяли ρk.
– коэффициент установки, определяли ρk.
Увеличивая разносы питающих электродов, последовательно в геометрической прогрессии и для каждого разноса рассчитывали ρk и строили кривые электрического зондирования (рис. 2). После переносили аппаратуру, оборудование на новую точку – и так для каждого региона проводили измерения. Результаты исследования регионов КЧР приведены в таблице.
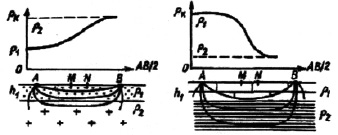
а) б)
Рис. 2. Двухслойные кривые электрического зондирования с ρ1 < ρ1 (а) и с ρ1 > ρ1 (б)
Результаты исследования регионов КЧР
|
№ п/п |
Регион |
№ образцов |
Возраст породы |
Название породы |
|
1 |
Верхне-Маринский, Карачаевский район, КЧР |
3/1066 |
γπPZ3 |
Железняк |
|
2 |
Правобережье р. Марухи, Зеленчукский район, КЧР |
2/1033 |
γπPZ3 |
Гранит-аплит |
|
3 |
Урупо-Власинчихинский комплекс, Зеленчукский район, КЧР |
9/1051 |
νPR-PZ1 |
Карбонат |
|
4 |
Учкуланское ущелье, Карачаевский район, КЧР |
19/1047 |
PZ1Kr |
Габбро |
Выводы
– Впервые исследованы и получены периодические электромагнитные поля для выявления полезных ископаемых, в частности магнитных горных пород (КЧР).
– Определены круговые колебания электромагнитных волн как результат сложения двух взаимно перпендикулярных колебаний с одинаковыми амплитудами и с разностью фаз π/2.
– Определена величина вектора магнитного поля H как сумма двух колебаний, одного с нулевой фазой и амплитудой, равной вещественной части |M0|, и другого, отличающегося от первого по фазе π/2 с амплитудой, равной мнимой части M0.
– Вычислены необходимые условия максимума и минимума для вектора М, а также определена его величина и направление.
– При помощи полученной математической модели выявлены полезные ископаемые в горных регионах КЧР.
Библиографическая ссылка
Урусова Б.И., Узденова Ф.А., Лайпанов У.М. ПЕРИОДИЧЕСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ, ПРИМЕНЯЕМЫЕ В ЭЛЕКТРОРАЗВЕДКЕ МАГНИТНЫХ ГОРНЫХ РУД // Успехи современного естествознания. 2019. № 3-2. С. 223-228;URL: https://natural-sciences.ru/ru/article/view?id=37097 (дата обращения: 19.01.2026).



