Рассмотрим математическую модель совместного существования двух биологических видов типа «хищник- жертва», называемую моделью Лотки- Вольтера. Пусть есть двабиологических вида, которые совместно обитают визолированной среде. Будем дляопределенности называть ихкарасями ищуками. Караси ищуки живут внекотором изолированном пруду. Среда предоставляет карасям питание внеограниченном количестве, ащуки питаются лишь карасями. Обозначим: у- число щук, х- число карасей.
Со временем число карасей ищук меняется, нотак какрыбы впруду много, тоне будем различать 1020 карасей или1021 ипоэтому будем считать хи унепрерывными функциями времени t. Будем называть пару чисел (х,у) состоянием модели. Рассмотрим, какменяется состояние (х, у) стечением времени. Пусть x’- скорость изменения численности карасей. Если щукнет, точисло карасей увеличивается итем быстрее, чембольше карасей. Будем считать, чтоэта зависимость линейная : x’ ~ε1 x, причем коэффициент ε1 зависит только отусловий жизни карасей, ихестественной смертности ирождаемости. Скорость изменения y’ числа щук(если неткарасей), зависит отчисла щукy. Будем считать, чтоy’~ε2 y, если карасей нет, точисло щукуменьшается (у нихнет пищи) иони вымирают. Вэкосистеме скорость изменения численности каждого вида пропорциональной егочисленности, нотолько скоэффициентом, который зависит отчисленности особей другого вида.
Так, длякарасей этот коэффициент уменьшается сувеличением числа щук, адля щукувеличивается сувеличением числа карасей. Будем считать этузависимость также линейной. Тогда получим систему издвух дифференциальных уравнений: x’ = ε1 x- γ1yx, y’ = -ε2 y+ γ2 xy.
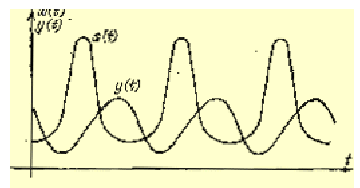
Эта система уравнений иназывается моделью Вольтерра-Лотки. Числовые коэффициенты ε1, γ1, ε2, γ2 называются параметрами модели. Очевидно, чтохарактер изменения состояния (x, y) определяется значениями параметров. Изменяя параметры ирешая систему уравнений модели можно исследовать закономерности изменения состояния экологической системы. Именно этопозволит вамсделать наша модель, которая находит решение уравнения Вольтерра- Лотки ивыводит кривые x(t) иy(t) награфик. Вкачестве примера нарисунке построены кривые изменения численности карасей xи щукy взависимости отвремени tдля некоторых типичных значений параметров. Максимумы кривых чередуются, причем максимумы щукотстают отмаксимума карасей. Этоотставание разное дляразных экосистем типа «хищник- жертва», но, какправило, много меньше периода колебаний.
В таблице показаны прогнозируемые результаты, полученные нами припомощи изученной модели. Этоколичество разведенной рыбы вКарельском водохранилище, приучете, чтопо нормам рыбоводства наодну тонну хищников приходится 2,5 тонны жертв.
|
2000 год |
2005 год |
2009 год |
|
|
Количество хищных рыб(т) |
16 |
18 |
17,5 |
|
Количество кормовых рыб(т) |
42 |
47,25 |
46 |
Библиографическая ссылка
Н.А. Петренко КОНТРОЛЬ ЧИСЛЕННОСТИ ВОДНЫХ ОБИТАТЕЛЕЙ ПРИ ПОМОЩИ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ // Успехи современного естествознания. 2010. № 10. С. 45-46;URL: https://natural-sciences.ru/ru/article/view?id=9079 (дата обращения: 17.01.2026).



