Вопрос надёжности программных средств имеет важнейшее значение. В настоящее время надёжность аппаратных средств, влияет на надёжность системы в целом меньше, чем надёжность программного обеспечения. Это связано с рядом причин: 1. Уровень технологий достаточно развит в плане создания высоконадёжных микросхем и вычислительных комплексов; 2. Стоимость серийно выпускаемых устройств снизилась значительно, что позволяет создавать резервные устройства, в качестве дублирующих.
Программные средства достаточно дороги, поскольку требуют высококлассных специалистов для их создания и, как правило, единичных экземпляров. Это не позволяет осуществлять полное резервирование программного продукта.
Вопрос получения надёжных алгоритмов программных средств, при современном бурном их распространении весьма актуален. Известны различные методы исследования и создания надёжных программных продуктов /1, 2/. В работе /3/ разработан метод исследования надёжности алгоритмов программного обеспечения на основе тензорной методологии. Тензорная методология позволяет не только исследовать, анализировать алгоритмы программного обеспечения с точки зрения надёжность, но синтезировать оптимальные схемы алгоритмов по критерию надёжности. В данном случае рассмотрим применение тензорного анализа к алгоритмам программного обеспечения ортогональной структуры рис. 1.
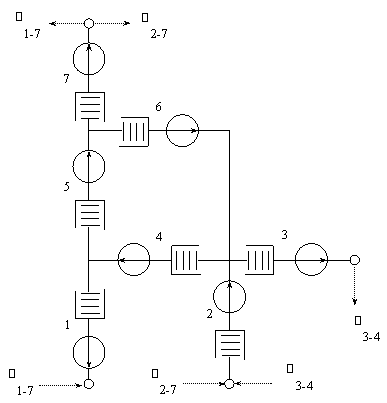
Рис.1. Исходный алгоритм ортогональной структуры
Суть тензорного метода заключается в том, что исходный алгоритм преобразуется в новую схему алгоритма, когда все блоки разнесены на большое расстояние, то есть, разорваны рис. 2. Исследования производят алгоритма простой схемы рисунок 2, а затем результаты переносят на исходный алгоритм рис. 1 по определённым правилам.
Тензорный анализ прост в вычислениях и сводится к простому умножению матриц /3/.
Важным достоинство метода является возможность анализировать большое схемы алгоритмов, на основе диакоптики. Метод обладает решением в прямом и обратном порядке, что позволяет от простой схемы рис. 2 перейти к сложной структуре наилучшей из всех возможных вариантов соединения с точки зрения её надёжности.
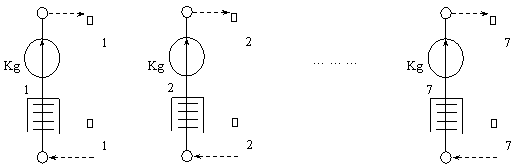
Рис. 2. Структура примитивной узловой схемы алгоритма из семи ветвей.
СПИСОК ЛИТЕРАТУРЫ:
- Русаков М.А., Р.Ю, Царев, С.А. Шабалин. Современные методы надежностной оценки сложных программных систем. - СПб.: Инфо-да, 2005 г.
- Ковалев И.В. Надежность архитектуры программного обеспечения телекоммуникационных технологий. - Международная науч. конф. Telematica´2001. Санкт-Петербург, 2001 г.
- Тензорная методология исследования надёжности алгоритмов программного обеспечениясистемдования социальных: Научное издание / Золотухин В.В., Колесов К.В., Петров М.Н.// Под ред. проф. М.Н. Петрова - Красноярск: НИИ СУВПТ, 2007 г. - 206 с.
Работа представлена на III научную международную конференцию «Фундаментальные исследования», Доминиканская республика, 10-20 апреля 2008 г. Поступила в редакцию 09.04.2008.



