В традиционной электродинамике хорошо известно строгое, но неявное решение данной задачи [1]. При этом электрон в поле плоской волны осциллирует и дрейфует [2], а также ускоряется в направление распространения волны. Последнее движение обусловлено явлением передачи заряду той части импульса поля волны, которая связана с энергией поля излучения электрона. Сила этого процесса равна усредненной силе реакции излучения <fS>, а её физической причиной выступает магнитная сила Лоренца [1].
В рамках модернизированной классической электродинамики появляется сдвиг фаз между E и H=B/μ0, вытекающий из базисных уравнений такого поля [3]. Поле плоской, однородной линейно поляризованной волны для частот ωτ<<1 будет
(1)
где τ - постоянная времени: параметр новых уравнений Максвелла.
Сдвиг фаз между E и H приводит к непосредственному влиянию магнитной силы Лоренца на поступательное движение заряженной частицы. Здесь изучается характер движения нерелятивистского электрона в поле (1) в лабораторной системе отсчета. Силой fS пренебрегаем, уравнение движения заряда q с массой m будет:
(2)
Переходим к обыкновенному уравнению относительно скорости vz
(3)
Уравнение (3) имеет аналитическое решение [4]. Пренебрегая изменением фазы волны
ψ = ω[t-z/c]=ω[t(1-v/c)-z(t0)/c] ≅ w[t-z(t0)/c]
и заменяя переменные
,
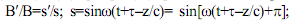
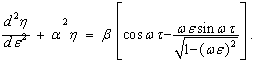(4)
Заметим, что в точках ω tk = (πk-ωτ+ωz/c), в которых s(tk) = 0, будет существовать решение уравнения (3), если удовлетворяется условие
Общее решение (4) известно
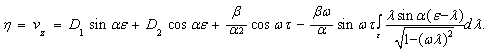(5)
Рассмотрим пример с нулевой начальной скоростью частицы при t=t0; vz(t0)=vx(t0)=0, тогда
из (2) az(t0)=0. Подставляя их в (5), имеем:
, (6)
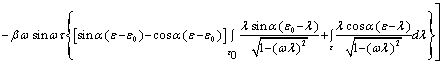(7)
Подставляя (7) во второе (2), получаем
,
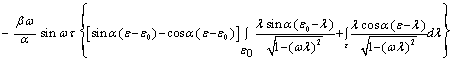(8)
,
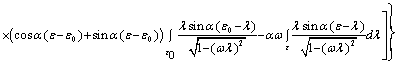(9)
где 
Выражения (6)-(9) правомерны при (v/c)<<1, это требует α/ω<< 1, поэтому, заменяя λ= - (cosφ)/ω, имеем:
;
.
Учитывая условие распространения волн ωτ<<1, приближенные выражения будут
, (10)
Вывод. В новой электродинамике (для традиционной τ=0), согласно (10), электрон в поле ЭМ волны колеблется в поперечном направлении с частотой ω, в продольном направлении - с частотой 2ω, а также дрейфует с постоянной скоростью, значение которой зависит и от начальных условий, и от начальной фазы волны ω(t0-z/c). В продольном направлении электрон также равномерно ускоряется силой
Проведем её сравнение с радиационной силой <fS>, и с продольной градиентной пондеромоторной силой <fРZ>, которая правомерна для неоднородной волны. Первая определяется в [1], вторая - в [5], тогда для радиоимпульса длительностью tu имеем:
, 
, 
.
Здесь: П1 - величина вектора Пойтинга волны, σ - полное сечение рассеяния и Р2 -мощность излучения электрона, τ0 = (r0/c)< τ, r0 - классический радиус электрона.
СПИСОК ЛИТЕРАТУРЫ:
-
Ландау Л.Д., Лифшиц Е.М. Теория поля, том. 2. - М.: Наука, 1973.- 504 с.
-
Болотовский Б.М., Серов А.В. Особенности движения частиц в электромагнитной волне // Успехи физических наук. - 2003. - Т. 173. - №6. - С. 667-678.
-
Меньшов Е.Н. Математическое моделирование электромагнитного поля: Деп. в ВИНИТИ от 25.10.2002, №1842 - В 2002. - 9 с.
-
Камке Э. Справочник по обыкновенным дифференциальным уравнениям: Пер. с нем. С.Ф. Фомина. - М.: Наука, 1976. - 576 с.
-
Федоров М.В. Электрон в сильном световом поле. - М.: Наука, 1991. - 223 с.