Системы управления, в том числе и когнитивные, опираются на представление о причинно-следственных связях и логику детерминизма, введённую ещё Аристотелем [2, 29 - 32]. Но уже Аристотель выявил, что введение детерминированных причинно-следственных связей с необходимостью приводит к фатализму, когда настоящее событие полностью предопределяет (является причиной) будущего следствия, и в свою очередь так же предопределено прошлой причиной, следствием которой является. Понимая это, Аристотель в своей силлогистики отказался от применения детерминистического описания будущих событий и применял детерминизм только для описания настоящих и прошлых событий. Столь нелогичный факт в логике привёл в XX веке к созданию модальных и многозначных логик, теории нечётких множеств, которые тем или иным путём пытались, оставаясь на детерминистических позициях, решить вопрос с логически корректным определением будущих событий.
Ни отказ от принципа детерминизма (который зарекомендовал себя в естественных науках), ни отказ от логики (булева логика широко применяется в автоматических и программно-управляемых устройствах), которые показали свою адекватность и работоспособность, не является удовлетворительным решением вопроса об определении будущих событий.
При рассмотрении логического фатализма возникают два вопроса. Первый вопрос. Почему логический вывод однозвенный? Именно однозвенность логического вывода и приводит к возникновению "нечувствительности" логического вывода к направлению между настоящим и будущим, настоящим и прошлым (их логическая эквивалентность). Второй вопрос. Почему причиной будущего события является единственное событие в настоящем, а не их совокупность? Именно единственность причины для данного следствию и является причиной фатализма. Как только причиной будущего события станет хотя бы два следствия прошлых причин, логический фатализм исчезает и появляется вариабильность будущих событий без нарушения строгости логического вывода. В результате можно предложить следующую схему (см. рисунок).
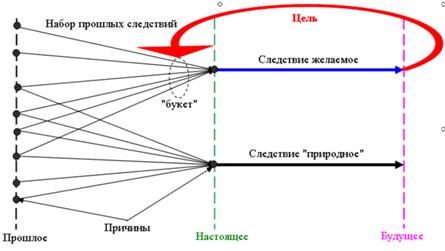
Рисунок. Вариант преодоление логического фатализма Аристотеля при формировании будущих событий
На рисунке точками обозначены причины, из которых формируются будущие следствия, векторы показывают переход от причин к следствиям. В данной схеме возникает логически строгая возможность, зная требуемые цели, целенаправленно собирать прошлые следствия в группы, чтобы сформировать причину будущего желательного события. Работу по сбору прошлых следствий в группы может производить как живой организм (благодаря биологическому механизму приспособления и адаптации), так и автоматическое устройство (обычные или самонастраивающееся).
Если предположить, что каждое следствие прошлых причин является величиной векторной, то в настоящем мы будем иметь не скалярный набор следствий, а векторное их поле, к которым применимы операции векторного сложения. Группируя эти векторные наборы в различные "букеты", мы тем самым обеспечим достижение заранее выбранного результата различными путями, с различными затратами ресурсов и временными характеристиками, различными векторами направленности будущих результатов. Будущий результирующий вектор "букета" является полной векторной суммой всех составляющих "букет" векторов. Построение многокорневого дерева решений в этом случае позволяет оценить полноту (необходимость и достаточность) собранных в "букет" следствий прошлых причин, для формирования причины будущего желаемого события.
Использование векторных величин вместо скалярных при сборе следствий в "букет" позволяет оценить энергию связи, которую необходимо приложить для того, чтобы удержать "букет" в собранном виде до тех пор, пока нужное следствие не запуститься и не станет самодостаточным (самостоятельным) в своём развитии.
Если воспользоваться потоковыми представлениями, а не векторными [3], то замена каждого вектора следствия потоком расширяет возможности по определению энергии связи собранных в "букет" следствий и позволяет учесть нелинейные характеристики взаимодействия потоков. Потоки, объединяемые в единый "букет", находясь в малой окрестности друг друга, могут как ослабляться, так и усиливаться. При этом возможны качественные системные эффекты, когда эффект суммы собранных в "букет" потоков превышает сумму эффектов каждого из потоков в отдельности.
То, что физические процессы имеют свойство группироваться, выявили исследователи циклов [1]. Этот же эффект подтвердился и на уровне микромира. В макромире наглядной иллюстрацией этого свойства служит распределение автомобилей по шоссе. Если посмотреть на шоссе сверху, то видно, что автомобили по нему движутся динамически формирующимися группами различного размера. Группы постоянно меняют свою конфигурацию, создаются (возникают), растут, уменьшаются, пульсируют в своих размерах, распадаются. Конкретные автомобили постоянно переходя из одной группы в другую. Между автомобилями нет прямых функциональных связей, но в группе они индуцировано вынуждены двигаться с одинаковой скоростью. Причина в том, что большинство автомобилей имеет примерно одинаковые характеристики, и у них недостаточно мощности, чтобы обогнать впереди идущую машину или этому мешает встречных поток автомобилей и автомобиль вынужденно остаётся на некоторое время в динамически сформировавшейся группе. Именно такие динамически формирующиеся "букеты" причин и запускают будущие следствия. В примере с автомобилями одни "букеты" являются причинами аварий в определённых местах шоссе («проклятые места»), или наоборот, способствуют равномерному распределению машин по шоссе. Исследование мест динамической группировки событий позволяет выявить локальные неоднородности процессов. А усилия по целенаправленному формированию в таких местах нужных «букетов причин» способствует запуску желательных будущих событий и исключения нежелательных. Тем самым преодолевается логический фатализм процесса (потока).
СПИСОК ЛИТЕРАТУРЫ:
- Владимирский Б.М., Темурьянц Н.А. Влияние солнечной активности на биосферу-ноосферую. Гелиобиология от А.Л. Чижевского до наших дней. М.: МНЭПУ, 2000. - 374 с.
- Карпенко А.С. Логика Лукасевича и простые числа. М.: Наука, 2000. - 319 с.
- Тупик Н.В. Общественные системы как поток / Сборник материалов научно-практи-ческой конференции "Управление ииновациями - 2007", М.: Доброе слово, ИПУ РАН, 2007, с.54 - 56.



