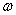кожуха транспортера, в котором спирально-винтовая пружина вращается около своей оси с постоянной угловой скоростью 
. Постоянный угол наклона винтовой линии пружины к плоскости поперечного сечения пружины равен 
.
К движущейся частице приложены силы:
- сила тяжести;
- нормальная реакция поверхности трубы транспортера;
- нормальная реакция поверхности проволочного витка пружины;
- сила трения частицы о поверхность трубы;
- сила трения частицы о поверхность проволочного витка пружины.
Направление сил за исключением силы трения частицы о поверхность трубы являются заданными. Угол θ между нормальной реакцией поверхности проволочного витка пружины и осью, перпендикулярной к винтовой линии, характеризует геометрические характеристики пружины, цилиндрического кожуха и размер частиц сыпучего материала в транспортере и определяется по формуле:
,
где r - внутренний радиус цилиндрического кожуха; r1 - радиус частицы; r2 - радиус пружины; d - диаметр проволоки.
Для определения направления силы трения необходимо знать положение касательной к траектории движения частицы по поверхности трубы транспортера, поскольку она направлена по этой касательной в сторону, обратную направлению скорости ее движения. Следовательно, направление данной силы трения будет меняться с изменением направления скорости движения частицы.
Отнесем движущуюся частицу материала к цилиндрическим осям координат 
, приняв левую системы отсчета. Тогда дифференциальные уравнения движения частицы в проекциях на оси координат можно записать, при условии, что 
:
,
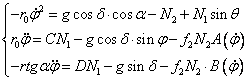где
,
,
,
.
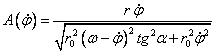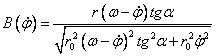