Настоящая работа имеет самое прямое отношение к проблеме создания так называемого вибрационного летательного аппарата. Это устройство представляет собой несимметричный корпус W, относительно которого совершает незатухающие, не обязательно гармонические, рабочее тело B (рисунок 1) [1,5].
Рисунок 1. Схема вибрационного летательного аппарата.
Качественно, если масса корпуса много меньше массы рабочего тела, подъемную силу F такого устройства можно оценить по формуле
![]() , (1)
, (1)
где a и T - амплитуда и период колебаний, соответственно, S -площадь сечения корпуса, r - плотность среды, cx - коэффициент аэродинамического сопротивления, соответствующий движению корпуса вниз, d - параметр асимметрии корпуса, представляющий собой, по существу, отношение величины cx к коэффициенту сопротивления, соответствующего движению корпуса вверх. Совершенно очевидно, что для увеличения подъемной силы необходим выбор параметров корпуса с максимально возможными значениями коэффициента сопротивления и параметра асимметрии. Это же требование вытекает и из строгого расчета [2]. Считается, что даже для полусферы параметр асимметрии составляет величину не менее 5 [6]. Это, впрочем, относится только к достаточно большим скоростям движения зонтообразного тела относительно среды и к статическому режиму, когда скорость воздуха относительно тела во время измерений остается неизменной. Первые серьезные испытания вибрационного способа полета оказались неудачными [3]. Одной из причин этого, как выяснилось, является низкое значение параметров асимметрии зонтообразных тел. Поэтому, измерение параметров асимметрии зонтообразных тел достаточно актуально для разработки и прогнозирования параметров вибрационного летательного аппарата.
Измерения силы сопротивления в аэродинамической трубе сложны, дорогостоящи и неоднозначны [4]. А для данной задачи вообще достаточно воспользоваться методом, основанным на точном измерении времени падения тела в среде с сопротивлением.
На рисунке 2 показаны результаты измерения времени падения t тонких лавсановых конусов с высоты h=0,67м для трех значений отношения площади боковой поверхности конуса SC к площади основания S.
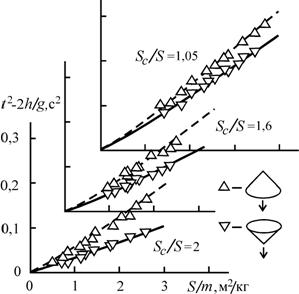
Рисунок 2. Зависимости времени падения конусообразных тел от отношения площади сечения к массе при различных площадях боковой поверхности SC. Точки - экспериментальные результаты, кривые - решение уравнения (2).
Точность измерения интервала времени составила величину не хуже 0,02с. Такой способ представления экспериментальных результатов выбран не случайно. Дело в том, что при квадратичном сопротивлении зависимость времени падения от массы тела m и площади сечения S определяется решением уравнения
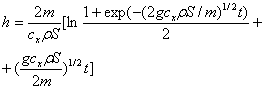 , (2)
, (2)
где r - плотность воздуха, g -ускорение свободного падения. Отсюда следует, что при фиксированном значении высоты время падения должно зависеть только от отношения S/m. В измерениях участвовали тонкие лавсановые конусы, падающие как острием вверх, так и вниз. Представленные на рисунке 2 результаты соответствуют изменениям площадей сечения тел более чем в 5 раз, масс - в 10 раз. При этом минимальное значение площади равнялось 0,02м2, а минимальная масса падающего тела - 0,02кг.
Следует обратить внимание на следующее обстоятельство. Падение всех конусов острием вниз происходит примерно с одним и тем же коэффициентом сопротивления. Его среднее значение - сx=2,7±0,3. Следующий факт: это значение незначительно отличается от коэффициентов сопротивления, соответствующих падению конусов острием вниз. Другими словами, даже при двукратном превышении площади боковой поверхности над площадью основания конуса параметр асимметрии составляет величину всего лишь 1,75. Коэффициенты сопротивления определялись из условия наилучшего соответствия зависимости t(S/m) полученным экспериментальным данным. Зависимость параметра асимметрии d от отношения площадей показана на рисунке 3.
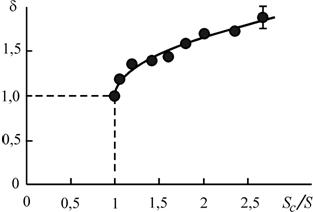
Рисунок 3. Параметры асимметрии конусообразных тел. Точки - экспериментальные результаты, сплошная кривая - зависимость (3).
Приближенно параметры асимметрии могут быть описаны выражением
![]() , (3)
, (3)
где b=0,65.
Это далеко не все, что можно извлечь из экспериментальных значений коэффициентов аэродинамического сопротивления. Например, можно определить оптимальный размер конусообразного корпуса вибрационного летательного аппарата. Действительно, подстановка полученного выражения (3) в (1) дает
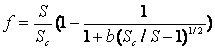
и позволяет определить оптимальное отношение S/SС. Здесь f=2T2F/p2a2cxrSC и представляет собой приведенную подъемную силу вибрационного летательного аппарата. Фиксированное значение площади боковой поверхности корпуса означает фиксированное значение массы вибрационного летательного аппарата. Поэтому имеет смысл рассмотреть зависимость приведенной подъемной силы от отношения площадей S/SС. Такая зависимость показана на рисунке 4 и демонстрирует, что приведенная подъемная сила максимальна при S/SС ≈ 2/3. При этом параметр асимметрии составляет d ≈1,5, причем f ≈ 0,2.
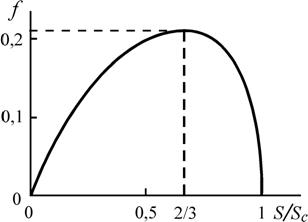
Рисунок 4. Зависимость приведенной подъемной силы f от отношения площади сечения к площади боковой поверхности конусообразного корпуса вибрационного летательного аппарата.
Например, при a=0,1м, T=0,1c и S=1м2 подъемная сила должна в лучшем случае составлять величину F≈5,2Н. Разумеется, это -завышенное значение. Однако теперь становится понятным, расчет критического режима вибрационного полета для больших параметров асимметрии [2] лишен смысла. Едва ли параметр асимметрии может составить величину больше 3. Попытки увеличить это число ведут к неоправданному утяжелению системы.
СПИСОК ЛИТЕРАТУРЫ
- Герасимов С.А. //Прикл. мех. и техн. физ. 2003. Т. 44. № 6. С. 44-48.
- Герасимов С.А., Удалова Е.С. //Техника и технология. 2005. № 1. С. 17-20.
- Герасимов С.А. //Естеств. и техн. науки. 2005. № 6. С. 128-132.
- Горлин С.М., Слезингер И.И. Аэромеханические измерения. - М.: Наука, 1964. - 720 с.
- Нагаев Р.Ф., Тамм Е.А. //Машиноведение. 1980. № 4. С. 3-8.
- Стрелков С.П. Механика. - М. Наука, 1975. - 560 с.



