Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Автором [1] показано, что работа подъема тела массы m в однородном поле силы тяжести на высоту h всегда больше потенциальной энергии . Нельзя поднять тело массой m силой тяги F_T, равной силе тяжести P=mg. В этом случае тело будет находиться в условиях статического равновесия, или в состоянии левитации (квазиневесомости). Любой противоестественный процесс (например, подъем тела вверх) требует затрат энергии больше, чем получаемая энергия (потенциальная), т.е. КПД процесса подъема всегда меньше единицы: , где  - работа подъема тела. В то же время естественный процесс свободного падения в вакууме соответствует закону сохранения энергии: , где  - работа, совершаемая силой тяжести при падении тела,  - кинетическая энергия тела в момент удара о Землю.

Чтобы поднимать тело вверх, необходимо приложить силу тяги , где  назовем силой левитации. Тело будет подниматься вверх с ускорением . За время t высота подъема будет равна . Работу, совершаемую силами F_T и P, будем определять в соответствии с методами, рассмотренными в работах [2,3,4], с использованием импульсов сил . Если сила постоянна, то импульс . Работа (производство энергии) может быть вычислена через импульс силы: . Тогда для нашего случая будем иметь

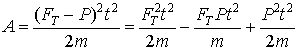                   (1)

Из выражения (1) выделим положительную работу , совершаемую силой тяги  и отрицательную  работу , совершаемую силой тяжести P=mg:

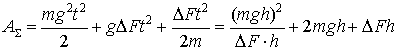                  (2)

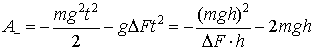                                       (3)

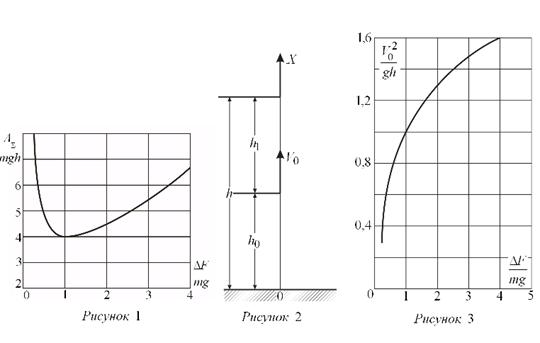
Выражение (2) имеет минимум, равный  при . На графике (рис. 1) показана зависимость работы , совершаемой силой тяги F_T, выраженной в долях потенциальной энергии , от величины соотношения . Сумма выражений (2) и (3) дает величину кинетической энергии, приобретенной телом на высоте h: . Чтобы остановить тело на высоте h, необходимо затратить работу торможения, равную этой кинетической энергии. Можно минимизировать работу подъема, создав на некоторой высоте h₀<h (рис. 2) скорость V₀, обеспечивающей подъем тела по инерции до высоты h при снятии на высоте h₀ силы тяги . Тогда затраты работы  сил  подъема  будут происходить только при движении до высоты h₀. Графически задача представлена на рис. 2. На высоте h₀ тело приобретает скорость V₀, затем силу тяги F_T отключают и остаток пути  тело пролетает по инерции, обладая запасом кинетической энергии , откуда . Скорость V₀ определяется из соотношений:

и .

Тогда выражение  можно представить в виде:

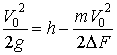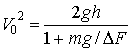      или                                             (4)

зависимость безразмерного комплекса  от соотношения  представлена на графике (рис. 3) и в таблице 1.

Таблица 1

В пределе при  комплекс  стремится к 2. Из равенства  определяется соотношение

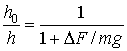                                       (5)

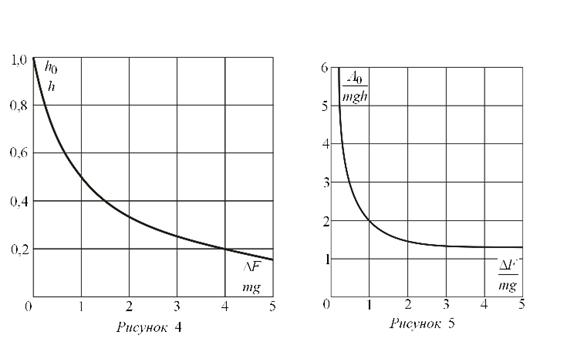
графическое представление которого показано на рис. 4.

Работа A₀, совершенная силой тяги F_T для  подъема на высоту h₀, будет определяться выражением

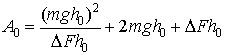                                      (6)

Зависимость безразмерного комплекса  от параметра  представлена на графике (рис. 5).

Из анализа соотношений (5) и (6) и графиков на рис. 4 и рис. 5 следует, что при  величина высоты h₀, на которой необходимо прикладывать силу тяги F_T, асимптотически стремится к нулю, а работа, совершаемая силой тяги F_T, на участке от X=0 до X=h₀, , т.е. только в этом предельном случае ( ) работа, затрачиваемая на подъем на высоту h, стремится к минимальному значению, равному потенциальной энергии .

СПИСОК ЛИТЕРАТУРЫ:

1. Иванов Е.М. Работа и энергия в классической механике и первый закон термодинамики. ДИТУД-УлГТУ, Димитровград, 2005.
2. Иванов Е.М. Работа в классической механике. // Современные наукоемкие технологии, №5, стр.12, 2005.
3. Иванов Е.М. Работа при движении тел с трением. // Фундаментальные исследования, №6, стр.10, 2005.
4. Иванов Е.М. Определение работы и работа силы трения. // Успехи современного естествознания, №8, стр.10, 2005.