Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Работу вычисляют по формуле: dA=FdS  или A=FS. Но эта формула применима только для силы вызывающей изменение кинетической энергии тела. Для других сил (трения, упругой деформации, центростремительных) работу нужно вычислять по формуле: , где  - импульс силы.

Work calculate under the formula: dA=FdS or A=FS . But this formula is applicable only for force of kinetic energy of a body causing change. For other forces (friction, elastic deformation, centripetal) work needs to be calculated under the formula: , where  - a pulse of force.

Из школьного курса известна формула для вычисления работы

 или                       (1)

полученная для результирующей силы, определяемой II законом Ньютона

                    (2)

В [1] это делается так. Переписывают уравнение (2) в следующем виде:

                        (2а)

Затем умножают правую часть на V, а левую на

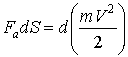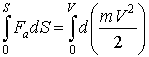 и                      (1а)

Для постоянной силы после интегрирования получают

 и                      (1в)

Последнее равенство комментируют так: «Изменение кинетической энергии материальной точки при её перемещении между двумя положениями равно работе, совершенной при этом силой».

I. Это утверждение справедливо только для случая свободного падения тела в однородном поле тяжести. Распространение его на другие случаи движения приводит к неправильному физическому смыслу: чтобы тело приобрело кинетическую энергию , надо затратить эквивалентную работу , т.е. коэффициент полезного действия процесса . Однако в природе таких процессов нет, всегда . Эта ошибка возникла потому, что в динамике нельзя использовать понятие материальной точки. Известно [2], что если на тело подействовать внешней силой, то прежде, чем оно придет в движение, произойдет деформация тела, возникнут силы упругости, т.е. часть работы внешней силы будет затрачена на работу упругой деформации. Силы (и работа)  деформации будут существовать до тех пор, пока тело движется с ускорением. После снятия нагрузки в деформированном теле возникают упругие колебания, которые вследствие дисперсии и внутреннего трения быстро затухают, переходя в теплоту (внутреннюю энергию). Таким образом, внешняя сила кроме работы разгона (создание кинетической энергии) всегда совершает и работу упругой деформации. Поэтому КПД всегда меньше единицы. Отметим, что задачи свободного падения тела и его подъем вверх не эквивалентны [12,13]. При свободном падении на тело действует одна массовая (объемная) сила - сила тяжести, и тело находится в недеформированном состоянии. При подъеме же тела вверх на него действуют две силы: объемная сила тяжести  и поверхностная подъемная сила F, под действием которых тело находится в деформированном состоянии. Таким образом, при подъеме вверх затрачивается дополнительная энергия на работу деформации тела [12].

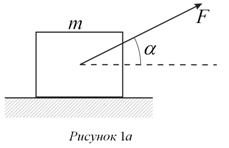
II. Далее кто-то предложил рассмотреть случай силы F, действующей на тело под некоторым углом к горизонту (рис.1а) и по аналогии с (1) записал формулу

 или                  (3)

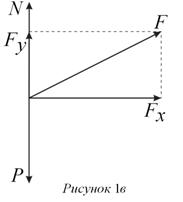
Отсюда и пошло определение работы как скалярного произведения двух векторов F и Ds. Однако формула (3) возникла в результате физической ошибки. Просто для случая (рис.1а) не была найдена результирующая сила F_a, входящая во второй закон Ньютона и, соответственно, в формулу (1). На тело m кроме силы F, действует ещё сила тяжести  и сила реакции опоры N (рис.1б), а результирующая всех сил , а . Если учесть ещё силы упругой деформации и силы трения, то результирующая сила F_a будет определяться более сложным выражением, чем , но это не означает, что для определения работы надо «изобретать» ещё одну, отличную от (3), формулу для вычисления работы. Формула для вычисления работы, затрачиваемой на изменение кинетической энергии тела, одна и только одна, и в ней не должно быть никакого ! Из-за этого  возникло много недоразумений. Так, утверждают, что если сила F перпендикулярна перемещению dS, то сила никакой работы не совершает, как и в случае, когда перемещение отсутствует - dS=0. Однако эти утверждения ошибочны, просто для вычисления работы нужна другая формула. Ведь формула (1) получена для работы результирующей силы F_a и не определяет работу других сил, входящих во II закон Ньютона (2). Утверждение о том, что какая-то сила не совершает работу - физический нонсенс. Если сила F действует на тело m в течении некоторого времени t, то эта сила всегда совершает работу (производит энергию), даже если dS=0 или .

III. Далее кто-то предложил для вычисления работы силы трения F_TP использовать формулу (1), заменив в ней индексы:

 или                (4)

Иначе, как математическим «беспределом», это назвать нельзя! Ведь вывод формулы (1) основан на преобразованиях (2а), (1а) и (1в) и связан с введением понятия кинетической энергии, а формула (4) записана без математического вывода, т.е. незаконно.

IV. Если на тело m действует горизонтальная сила F, то часть её расходуется на преодоление силы трения F_TP, а оставшаяся часть F_a на изменение кинетической энергии, т.е. . Кто-то предложил работу силы F рассматривать как арифметическую сумму работ сил F_a и F_TP

                       (5)

Проведем численный расчет для анализа справедливости формулы (5). Действие силы будем определять импульсом силы: . Для постоянной силы . Пусть на тело массы m=10 кг действует горизонтальная сила F=100 Н в течение времени  с, т.е. действует импульс силы I=1000 Н·с. Коэффициент трения скольжения . Расчет произведем для двух случаев: с трением и без трения. Расчет сведем в Таблицу 1.

Таблица 1.

Из таблицы следует, что один и тот же импульс силы  Н·с, воздействуя на одно и то же тело m=10 кг, производит разное количество энергии (работы): 50 и 40 кДж. Куда же «исчезла» энергия? Следует усомниться в справедливости выражений (4) и (5). Это рассмотрено в работах [9-11, 14, 15]

V. Формулы (1) и (1в) можно преобразовать, если использовать соотношение

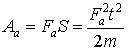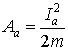. Тогда  или         (6)

Таким образом, работу  можно рассчитывать по импульсу силы, без использования пути S, определяя работу как энергетический комплекс .

VI. Вернемся к формуле (2а). Она гласит: «Приращение количества движения (импульса тела ) равно изменению импульса силы ». Интегрируя (2а) для случая постоянной силы, получим . Возведя в квадрат и разделив на обе части равенства, получим

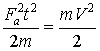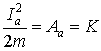 или             (7)

Таким образом, энергетический комплекс  может быть использован для вычисления работы, совершаемой импульсом силы и в случае отсутствия перемещения (dS=0 ) и в случае силы, перпендикулярной перемещению. Так, для случая движения тела с трением, рассмотренном в разделе IV, имеем  Н. Тогда работа будет равна

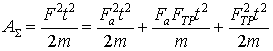              (8)

В численном виде получим  кДж, т.е. получили такую же работу, как и в случае движения без трения. Отметим, что работа силы трения состоит из двух частей:  - работа при ускоренном движении и  - работа при равномерном движении.

VII. Известно, что работа сил трения переходит в теплоту, т.е. происходит повышение внутренней энергии  контактных слоев трущихся тел. Тогда выражение (8) можно представить в следующем виде:

             (9)

где  - производство энергии импульсом силы,  работа, затрачиваемая импульсом силы F_a на разгон тела m,  - изменение внутренней энергии.

Таким образом, выражение (9) представляет собой не что иное, как I закон термодинамики в применении к механическим процессам. Само же выражение (8) записано на основе суммы векторов импульсов сил , которую можно переписать с использованием теоремы косинусов:

                  (10)

Разделив обе части равенства (10) на 2m, получим баланс энергий в виде равенства (8), которое следует использовать вместо равенства (5).

VIII. В курсах физики при рассмотрении так называемых «потенциальных» полей при перемещении тела заряда из точки 1 в точку 2 рисуют несколько произвольных траекторий и утверждают, что работы перемещения одинаковы, т.к. 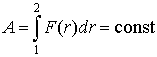, а работа по замкнутому контуру .

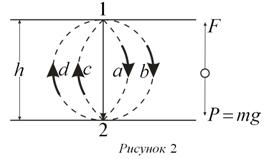
Рассмотрим однородное поле силы тяжести (рис.2), в котором силовые линии направлены сверху вниз (например, прямая 1-2). Под действием сил поля тело будет двигаться только по вертикальной линии 1-2, при этом потенциальная энергия  переходит в кинетическую . Если тело перемещается по криволинейной траектории (например, 1а2 или 1в2), то для этого необходимо ещё действие других (сторонних) сил, которые совершают дополнительную работу.

Для перемещения тела в обратном направлении (по прямой 2-1) необходимо приложить силу , т.к. невозможно поднять тело вверх силой, равной силе тяжести (будет статическое равновесие). Поднимая тело силой , мы совершаем равноускоренное движение. Время перемещения , а затрачиваемая работа будет равна

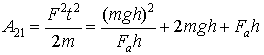                (11)

Эта работа имеет минимум, равный  при . Отрицательная работа, совершаемая силой тяжести при подъеме тела вверх, по модулю равна первым двум слагаемым выражения (11). При  она равна , а разность положительной (11) и отрицательной работ, равная , затрачивается на создание кинетической энергии .

IX. Автором [6-8] впервые было введено понятие работы поворота. Из закона инерции Галилея (I закон Ньютона) следует [3]: всякое тело оказывает сопротивление при попытках привести его в движение или изменить модуль или направление его скорости. Это свойство тел называется инертностью. Чтобы преодолеть сопротивление, необходимо приложить усилие, т.е. совершить работу. Однако до сих пор работа поворота не была определена.

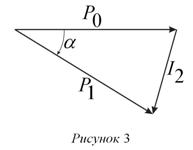
Пусть брусок массы m движется прямолинейно со скоростью V₀ по гладкой поверхности, т.е. он обладает импульсом (количеством движения) . Изменим направление движения без изменения модуля скорости на некоторый угол . Для этого нанесем по одному из концов бруска сверхкороткий удар в виде действия мгновенной силы , т.е. передадим единичный импульс силы  (рис.3), где  - дельта-функция Дирака [5]. Из векторной суммы  с помощью теоремы косинусов находим , т.к. по модулю . Тогда работу поворота тела массы  при постоянной скорости V₀ на угол  от первоначального направления движения можно записать в виде

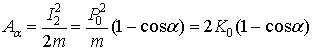;         (12)

где . Для углов поворота, больших чем , например , учитывая периодичность функции косинуса, надо к работе поворота на угол  добавить работу . Формулу (12) можно использовать для вычисления работы центростремительных сил при равномерном движении тела (заряда) по окружности [6-8].

СПИСОК ЛИТЕРАТУРЫ:

1. Матвеев А.Н. Механика и теория относительности. М.: Высшая школа, 1986.
2. Элементарный учебник физики. Том I. Под ред. акад. Ландсберга Г.С. М.: Наука, 1972.
3. Сивухин Д.В. Общий курс физики. Том I. Механика. М.: Наука, 1989.
4. Стрелков С.П. Механика. М.: ГИТТЛ, 1956.
5. Арсенин В.Я. Математическая физика. М.: Наука, 1966.
6. Иванов Е.М. Работа центростремительных и гироскопических сил//Вестник ДИТУД, №1, Димитровград, 2003, с.66.
7. Иванов Е.М. Работа центростремительных и гироскопических сил//Успехи современного естествознания, №9, 2004.
8. Ivanov E.M. Work of centripetal and gyroscopic forces. // European Journal of Natural History, № 1, 2006, P.80.
9. Иванов Е.М. и энергия в классической механике и I закон термодинамики // Фундаментальные исследования, №8, 2005, С.11.
10. Иванов Е.М. Работа при движении тел с трением // Фундаментальные исследования, №6, 2005, С.10
11. Иванов Е.М. Определение работы и работа силы трения // Успехи современного естествознания, №8, 2005, С.10
12. Иванов Е.М. Работа подъема тела в однородном поле тяжести // Современные наукоемкие технологии, №3, 2005, С.9
13. Иванов Е.М. Работа падения тела в однородном поле тяжести // Современные проблемы науки и образования, №4, 2006, С.11
14. Иванов Е.М. Как вычислить работу // Успехи современного естествознания, №11, 2005, С.9
15. Иванов Е.М. Об аддитивности работ в классической механике. // Успехи современного естествознания, №12, 2005, С.10