Проблема исследований: Применение адаптивных средств защиты информации (АСЗИ) позволит повысить эффективность защиты информации от НСД. В то же самое время обеспечение надежности функционирования спецпроцессоров (СП) АСЗИ является одной в ряду наиболее важных задач.
Решение проблемы:
При хранении, передаче и обмене электронной информацией в сетях и системах возникают проблемы обеспечения ее конфиденциальности и целостности. Решить данную задачу можно за счет применения адаптивных средств защиты информации. Применение алгебраических систем, определяемых в расширенных полях Галуа, является одним из наиболее перспективных направлений в построении АСЗИ. В таких системах основными криптографическими преобразованиями являются сложение, умножение и возведение элементов по модулю порождающего полинома g(z). Применение полиномиальной системы классов вычетов (ПСКВ) позволяет повысить не только скорость проведения криптографических преобразований, но и обеспечить высокую надежность работы СП АСЗИ.
Согласно [1-3] в данной алгебраической системе полином A(z), удовлетворяющий условию 
где 
, представляется в виде вектора
, (1)
где 
, 
- минимальные многочлены расширенного поля 
, 
.
Тогда операции сложения, вычитания и умножения можно свести к операциям, проводимым над соответствующими остатками, что повышает быстродействие. Кроме того операции проводятся над малоразрядными операндами, что позволяет сократить аппаратурные затраты.
Однако применение ПСКВ позволяет не только повысить скорость обработки данных, но и обеспечить высокую надежность работы СП [1-3]. Если на диапазон возможного изменения кодируемого множества полиномов наложить ограничения, то есть выбрать k из n оснований ПСКВ (k<n ), то это определит рабочий диапазон
, (2)
Многочлен X(z) будет считаться разрешенным, если он принадлежит рабочему диапазону 
. Если полином не принадлежит этому диапазону, то он содержит ошибки.
Для коррекции ошибок в немодулярных кодах широко используются позиционные характеристики [3]. Среди множества алгоритмов определения позиционной характеристики непозиционного кода полиномиальной системы класса вычетов особое место принадлежит алгоритму обнаружения ошибки, базирующемуся на процедуре расширения оснований ПСКВ.
, (3)
где Bi(z) - ортогональный базис по i-ому основанию; i=1,...,k.
Для расширенной системы оснований 
справедливо
, (4)
где 
- ортогональный базис в расширенно системе оснований; 
- ранг, 
- рабочий диапазон.
Если положить условие, что 
, то
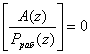. (5)
Тогда, подставив в равенство (4) выражение (5) получаем
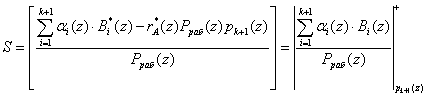, (6)
где S - номер интервала.
Исходя из условия взаимной простоты оснований имеем
(7)
Так как 
, то выражение (4) можно представить
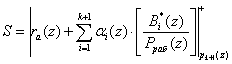. (8)
Положив, что 
, получаем
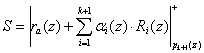. (9)
Если S=0, то значение . В противном случае
, (10)
где 
.
Тогда
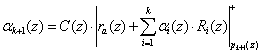. (11)
Затем значение остатка по контрольному основанию, вычисленное согласно (11), сравниванию с остатком, полученным в процессе работы СП АСЗИ. Если данные значения совпадают, то это свидетельствует о том, что исходная комбинация ПСКВ не содержит ошибки. В противном случае - комбинация ПСКВ содержит ошибку, вызванную отказом оборудования СП.
Применение алгоритма расширения оснований позволяет исправлять однократные ошибки, возникающие в результате отказов работы спецпроцессора криптографических преобразований.
СПИСОК ЛИТЕРАТУРЫ:
- Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов/ Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2005. - 276 с.
- Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронных сетей для исследования ортогональных преобразований в расширенных полях Галуа/Нейрокомпьютеры: разработка, применение. №6, 2003. с.61-68с.
- Элементы применения компьютерной математики и нейроинформатики /Н.И. Червяков, И.А. Калмыков И.А., В.А. Галкина, Ю.О. Щелкунова, А.А. Шилов; Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2003. - 216 с.