Проблема исследований: В ближайшем будущем роль компьютерных систем будет всемерно усиливаться. При этом возникают новые задачи по разработке и созданию адаптивных средств защиты информации (АСЗИ) в вычислительных сетях от несанкционированного доступа (НСД).
Решение проблемы:
В последние годы наблюдается тенденция все более всестороннего применения алгебраических систем, определяемых в расширенных полях Галуа, при построении адаптивных средств защиты информации. Это обуславливает возможность использования следующих криптографических преобразований:
- сложение элементов по модулю порождающего полинома g(z);
- умножение элементов поля по модулю порождающего полинома g(z);
- возведение элементов в степень по модулю g(z).
Применение полиномиальной системы классов вычетов (ПСКВ) позволяет повысить эффективность данных систем с точки зрения обеспечения высокой скорости работы криптографического устройства.
Если в качестве оснований алгебраической системы выбрать минимальные многочлены ![]() поля
поля ![]() , то полином A(z), удовлетворяющий условию
, то полином A(z), удовлетворяющий условию ![]() где
где ![]() , представляется в виде вектора
, представляется в виде вектора
![]() , (1)
, (1)
где ![]() ,
, ![]() .
.
Для двух полиномов, принадлежащих полному диапазону A(z) = ![]() и B(z) =
и B(z) = ![]() , справедливо [1,2]:
, справедливо [1,2]:
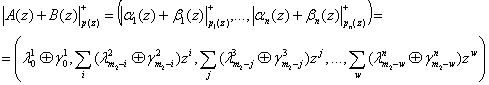 , (2)
, (2)
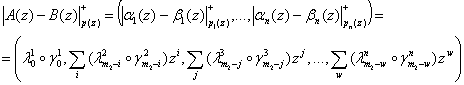 , (3)
, (3)
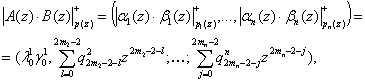 (4)
(4)
где ![]() - линейная свертка;
- линейная свертка; ![]() ,
, ![]() .
.
Следовательно, ПСКВ может быть использована при реализации криптографических преобразований.
Пусть для выработки М-последовательности задан порождающий полином ![]() , а для реализации криптографических преобразований в поле GF(27) - порождающий полином
, а для реализации криптографических преобразований в поле GF(27) - порождающий полином ![]() . Тогда для одновременного обеспечения информационной скрытности и высокой скорости работы спецпроцессора АСЗИ будут использоваться 7-разрядные элементы поля GF(27). В этом случае сформированная последовательность символов в виде двоичных векторов длиной 7 бит является псевдослучайной последовательностью (ПСП) элементов конечного поля GF(27). Так как сформированная последовательность является последовательностью элементов мультипликативной группы расширенного поля Галуа GF(27), то к ним возможно применение криптографических преобразований.
. Тогда для одновременного обеспечения информационной скрытности и высокой скорости работы спецпроцессора АСЗИ будут использоваться 7-разрядные элементы поля GF(27). В этом случае сформированная последовательность символов в виде двоичных векторов длиной 7 бит является псевдослучайной последовательностью (ПСП) элементов конечного поля GF(27). Так как сформированная последовательность является последовательностью элементов мультипликативной группы расширенного поля Галуа GF(27), то к ним возможно применение криптографических преобразований.
Пусть криптографические преобразования определяются выражением
![]() . (2)
. (2)
В таблице представлено состояние первых 15 ячеек памяти генератора двоичной ПСП, задаваемой порождающим полиномом ![]() .
.
Таблица 1
|
№ |
Ячейки памяти генератора М-последовательности |
||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
2 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
Так как для реализации (2) необходимо две ПСП элементов поля GF(27), то значение первой ПСП снимаем с первой по седьмую ячеек, согласно выражения
![]() , (3)
, (3)
а значение второй ПСП с восьмой по четырнадцатую ячеек генератора М-последовательности
![]() . (4)
. (4)
Тогда имеем следующие элементы поля GF(27) на первых двух тактах работы генератора:
1 такт g11(z)=0110001=z5+z4+1 ; g21(z)=1100110=z6+z5+z2+z ;
2 такт g12(z)=1100011=z6+z5+z+1; g22(z)=1001100=z6+z3+z2;
Пусть в качестве открытого текста используется 7-битовая последовательность
s(z)=0000011=z+1.
Проведем преобразования согласно (2). Получаем
![]()
В качестве ПСКВ выберем алгебраическую систему, определяемую основаниями: ![]() ;
; ![]() ,
, ![]() . Тогда рабочий диапазон составляет
. Тогда рабочий диапазон составляет ![]() . Представим исходные последовательности в коде ПСКВ и проведем соответствующие преобразования:
. Представим исходные последовательности в коде ПСКВ и проведем соответствующие преобразования:
Операнды |
|
α1(z) |
α2(z) |
α3(z) |
α4(z) |
α5(z) |
|
s(z)=z+1 |
х |
0 |
z+1 |
z+1 |
z+1 |
z+1 |
|
g11(z)=z5+z4+1 |
1 |
0 |
z3+z2+z+1 |
z+1 |
z2 |
|
|
|
+ |
0 |
0 |
z3+z2+z |
z2+1 |
z3+z2 |
|
g21(z)=z6+z5+z2+z |
0 |
z+1 |
z2+1 |
z |
z3+z2 |
|
|
|
|
0 |
z+1 |
z3+z+1 |
z2+z+1 |
0 |
Таким образом, имеем
![]()
Следовательно, применение ПСКВ позволяет обеспечить следующие преимущества [1,3]:
- операции выполняются над остатками независимо по каждому из модулей pi(z), что позволяет повысить быстродействие вычислительной системы;
- операции проводятся над малоразрядными операндами, что позволяет не только повысить быстродействие системы, но и сократить аппаратурные затраты.
СПИСОК ЛИТЕРАТУРЫ:
- Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов /Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2005. - 276 с.
- Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Бережной В.В. Математическая модель нейронных сетей для исследования ортогональных преобразований в расширенных полях Галуа /Нейрокомпьютеры: разработка, применение. №6, 2003. с.61-68с.
- Элементы применения компьютерной математики и нейроинформатики /Н.И. Червяков, И.А. Калмыков И.А., В.А. Галкина, Ю.О. Щелкунова, А.А. Шилов; Под ред. Н.И. Червякова. - М.: ФИЗМАТЛИТ, 2003. - 216 с.



