Математическому моделированию процессов конкуренции и сотрудничества двух фирм на различных рынках посвящено довольно много научных работ, в основном использующих аппарат теории игр и статистических решений. В качестве примера можно привести работы таких исследователей, как Курно, Стакельберг, Бертран, Нэш, Парето, основные результаты которых приведены в [1-2,5].
В настоящей работе авторами предпринята попытка математического моделирования конкурентной борьбы с точки зрения экономической динамики с привлечением аппарата теории оптимального управления.
Изменение объемов продаж конкурирующих фирм с течением времени может быть описано следующей системой дифференциальных уравнений [4]:
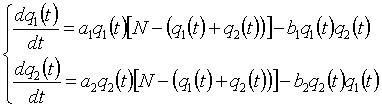(1)
с начальными условиями 
. (2)
Здесь и далее использованы следующие обозначения:
q1(t) - объем продаж фирмы I;
q2(t) - объем продаж фирмы II;
N - объем рассматриваемого сегмента рынка сбыта;
a1, b1, a2,b2 -положительные коэффициенты, характеризующие степень влияния различных факторов на изменения объема продаж первой и второй фирмы соответственно [4].
Замена переменных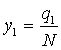 
, 
, 
; 
, 
, 
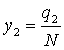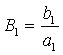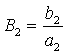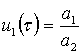приводит исходную задачу Коши к безразмерному виду:
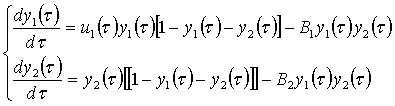(3)
Функция 
характеризует степень воздействия внутренней среды первого предприятия на рост объемов продаж по отношению к аналогичной величине конкурента.
Неизбежно возникает вопрос о минимизации управленческого воздействия первого предприятия, необходимые для достижения к известному моменту времени T заранее запланированной рыночной доли 
, ответ на который может быть, по мнению авторов, получен из решения следующей задачи оптимального управления, которая и является предметом исследования данной работы: найти такое программное управление 
, которое доставляет минимум целевому функционалу
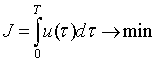, (4)
удовлетворяет системе дифференциальных уравнений с граничными условиями (3) и ограничениями на состояние системы и управление:
, 
, 
, 
, 
, где 
. (5)
Здесь 
- желаемая рыночная доля первого предприятия в этот же момент времени, а значение 
выбиралось из следующих соображений: пусть предприятие для достижения поставленной цели располагает ресурсами Q, а величина 
может трактоваться как скорость расходования ресурсов предприятия. Следовательно, 
. Следует, однако, отметить, что это далеко не единственный способ выбора этой величины.
Алгоритм численного решения задачи (4)-(5) основан на отмеченной рядом исследователей [5] глубокой связью между задачами оптимального управления и математического программирования. С этой точкой зрения задача оптимального управления для непрерывной системы образует бесконечномерную задачу математического программирования в бесконечномерном пространстве. Основным достоинством данного подхода является возможность применения хорошо развитого аппарата численного решения задач математического программирования к теории оптимального управления.
Следуя указанному подходу [5], переформулируем задачу в дискретной форме. Временной интервал 
разбивается на n равных временных интервалов, целевой функционал (4) заменяется интегральном суммой, а задача Коши (3) -конечно-разностной аппроксимацией, основанной на интерполяционных уравнениях Адамса [5].
В результате получаем задачу нелинейного программирования, в которой целевому функционалу соответствует целевая функция, а уравнение состояния превращается в 2n ограничений в форме равенств.
Ограничения на состояние системы и управления трансформируются в ограничения в форме неравенств задачи математического программирования:
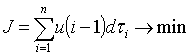(6)
,
,
(
)
; 
; 
; ; 
;
; . (7)
Здесь:
; 
; 
.
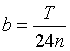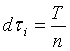Задача решалась численно с помощью надстройки «Поиск решения» пакета Microsoft Office Excel 2003 по встроенному алгоритму нелинейной оптимизации Generalized Reduced Gradient (GRG2), разработанному Леоном Ласдоном (Leon Lasdon, University of Texas at Austin) и Аланом Уореном (Allan Waren, Cleveland State University).
В результате в каждой точке находились 
, y1(i), y2(i), а также значения целевого функционала J.
Точность полученного решения оценивалась «апостериори» путем подстановки найденного программного управления u=u(t) в (3) с последующим численным интегрированием системы ОДУ методом Рунге-Кутта четвертого порядка [3].
Некоторые результаты численных расчетов приведены на рис.1-3. При построении графиков использовались следующие значения параметров модели: 
; n=20; 
; 
; 
.
Значение T варьировалось в пределах от 2 до 3.
Анализ рис. 1 позволяет сделать вывод об адекватности построенной математической модели и достаточной точности аппроксимации исходной задачи оптимального управления (3)-(5) задачей нелинейного программирования (6)-(7).
Об этом свидетельствует тот факт, что непрерывные кривые, построенные по результатам численного интегрирования задачи Коши (3) практически совпадают с точками, соответствующими решению конечно-разностной задаче нелинейного программирования.
Рис. 2 указывает на то, что во всех случаях поведение оптимального программного управления 
обнаруживает следующую характерную особенность: до определенного момента времени 
, после чего резко падает до нуля. По результатам численных экспериментов 
.
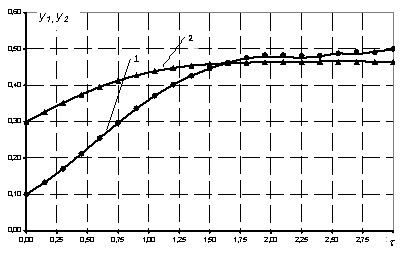
Рис.1. Оптимальная динамика объема продаж фирмы I и фирмы II для T=3. Сплошные линии соответствуют результатам контрольного интегрирования методом Рунге-Кутта.
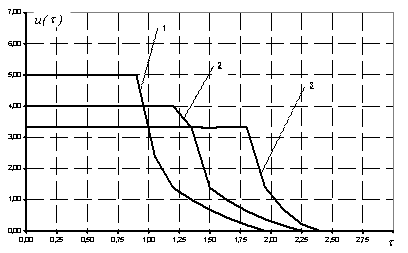
Рис.2. Зависимость оптимального управления от времени для случаев T=2,0 (кривая 1), T=2,5 (кривая 2), T=3,0 (кривая 3). Выделенные ресурсы Q=10,0.
Рис.3. Зависимость оптимального значения целевого функционала J от ресурсов Q для T=2.
Это позволяет сделать практически важный вывод о том, что оптимальная стратегия предприятия по достижению желаемой рыночной доли в условиях дуополии заключается в приложении максимальных усилий именно на начальном участке, после чего, начиная с момента времени , можно значительно уменьшить интенсивность расхода ресурсов.
Зависимость оптимального значения целевого функционала J, от выделенных ресурсов Q представлена на рис. 3. Убывающий характер этой зависимости объясняется тем, что с увеличением Q возрастает , а значит, и интенсивность использования ресурсов на начальном, «стартовом» участке траектории динамической системы. А поскольку именно этот участок является наиболее важным с точки зрения достижения желаемого результата, в конечном итоге это приводит к интегральному эффекту экономии ресурсов.
СПИСОК ЛИТЕРАТУРЫ:
- Бережной Л.И. Теория оптимального управления экономическими системами: Учебное пособие. - СПб.: ИВЭСЭП, Знание,2002. 64 с.
- Ванько В.И., Ермошина О.В., Кувыркин Г.Н. Вариационное исчисление и оптимальное управление: Учеб. для вузов. 2-е изд./ Под ред. В.С. Зарубина, А.П. Крищенко.-М.: Изд-во МГТУ им. Баумана, 2001. 488 с.
- Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. Томск: МП «Раско», 1991. 272 с. ил.
- Просвиров А.Э. Копылов А.В., Динамическая модель конкуренции двух фирм на однородном рынке // Успехи современного естествознания, №8, 2003. стр. 29-33.
- Табак Д., Куо Б. Оптимальное управление и математическое программирование, перев. с англ. М., Наука, 1975. 280 с.