Введение
При моделировании микроускорений с помощью действительной части фрактальной функции Вейерштрасса-Мандельброта (ФВМ) [1]:
(1)
важно грамотно провести отождествление параметров функции (1) и реальных условий процесса возникновения поля микроускорений внутри КА.
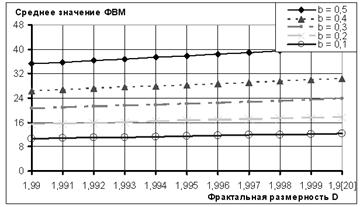
Рисунок 1. Динамика изменения среднего значения ФВМ
Этой теме, равно как и возможности использовании ФВМ в виде (1) при тождественно равной нулю случайной фазе, посвящен ряд работ [2-5], с которыми можно ознакомиться для понимания решаемой задачи. В работе [4] были получены корреляционные зависимости между средним значением ФВМ (1) и фрактальной размерностью D (рис. 1).
Как видно из рис. 1, они практически линейны. Этот факт доказывается с помощью коэффициента детерминации, который при оценке качества моделирования корреляционных зависимостей рис. 1 во всех случаях превышает 0,999 (рис. 2).
Как видно из рис. 1, они практически линейны. Этот факт доказывается с помощью коэффициента детерминации, который при оценке качества моделирования корреляционных зависимостей рис. 1 во всех случаях превышает 0,999 (рис. 2).
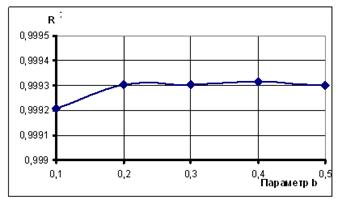
Рисунок 2. Зависимость коэффициента детерминации от параметра b при моделировании корреляционных зависимостей рис.1 линейной моделью парной регрессии
Постановка задачи
Для построения функциональной зависимости между фрактальной размерностью ФВМ D и средним значением ФВМ (1) с помощью линейной модели парной регрессии вида:
(2)
требуется исследовать влияние параметра b ФВМ на коэффициенты 
и 
правой части (2), исходя из полученных ранее корреляционных зависимостей рис. 1.
Основные результаты работы
Как видно из рис. 1, оба исследуемых коэффициента с ростом b изменяются. Для аппроксимации корреляционной зависимости и b (рис. 3)
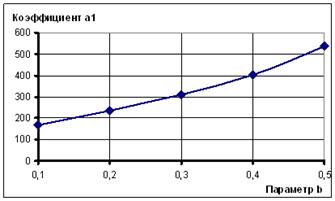
Рисунок 3. Корреляционная зависимость коэффициента а1 от параметра b
Была сначала построена линейная модель:
(3)
и с помощью метода наименьших квадратов (МНК) оценены коэффициенты 
и 
, которые получились равными:
;
. Таким образом, наилучшая с точки зрения МНК линейная зависимость коэффициента от b имеет вид:
(4)
Затем была предпринята попытка улучшить качество аппроксимации за счет учета квадратичного члена, заменив зависимость (3) на квадратичную вида:
, (5)
для которой также с помощью МНК были оценены коэффициенты:
;
;
. Таким образом, наилучшая с точки зрения МНК квадратичная зависимость коэффициента от b имеет вид:
(6)
И, наконец, был произведен учет кубического члена с помощью зависимости:
, (7)
При этом коэффициенты, найденные с помощью МНК, оказались равными:
;
;
;
.
Таким образом, наилучшая с точки зрения МНК кубическая зависимость коэффициента от b имеет вид:
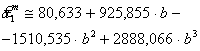(8)
Качество построенных зависимостей (4), (6) и (8) проверялось с помощью коэффициента детерминации (рис. 4) и критерия согласия 
-Пирсона (рис. 5).
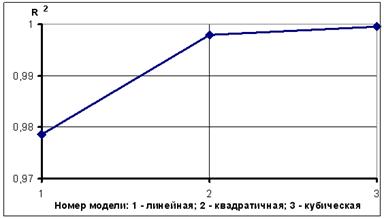
Рисунок 4. Изменение коэффициента детерминации при усложнении формы модели зависимости коэффициента а1 от параметра b
Усложнение модели связано, прежде всего с высоким качеством аппроксимации корреляционных зависимостей рис. 1 моделью (2). Значения коэффициентов детерминации для линейной и квадратичной моделей составили 0,979 и 0,998 соответственно, что ниже значений коэффициентов детерминации, рассчитанных при моделировании (рис. 2). И только модель (8) позволяет с уверенностью сделать вывод о том, что потерь качества при замене коэффициента на правую часть (8) не будет, т.к. значение коэффициента детерминации составляет 0,9995.
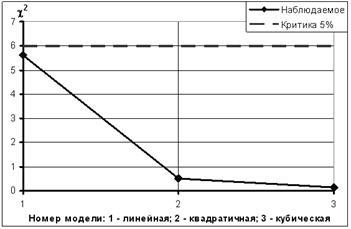
Рисунок 5. Динамика изменения наблюдаемого значения критерия согласия при усложнении модели
Критерий согласия еще более наглядно показывает улучшение качества моделирования при усложнении формы модели. Критическое значение критерия для рассматриваемых двух степеней свободы равно 5,99147 (5 %-й уровень значимости). Наблюдаемое значение критерия для линейной модели (4) составляет 5,613, что очень близко к критическому, несмотря на высокое значение коэффициента детерминации. Для квадратичной модели (6) величина наблюдаемого значения критерия сокращается более, чем в десять раз: 0,505 и почти в четыре раза сокращается еще для кубической модели (8): 0,130.
Таким образом, проверка качества построенных моделей (4), (6) и (8) показала, что лишь последняя из них достаточно точно описывает динамику изменения коэффициента 
в модели (2).
Следующим этапом является исследование зависимости другого параметра модели (2) от b. При замене корреляционных зависимостей рис.1 на функциональные вида (2) была построена зависимость изменения при различных значениях b. Эта зависимость приведена на рис. 6.
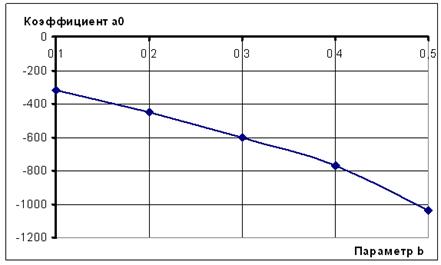
Рисунок 6. Корреляционная зависимость коэффициента а0 от параметра b
Аналогично схеме построения зависимости от b, сначала была исследована линейная зависимость, подобная (3). С помощью МНК подобраны коэффициенты этой модели:
(9)
Затем были подобраны лучшие с точки зрения МНК коэффициенты квадратичной зависимости, подобной (5):
(10)
и кубической зависимости, подобной (7):
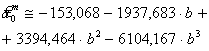(11)
Качество построенных моделей (9), (10) и (11) оценивалось с помощью коэффициента детерминации (рис. 7) и критерия согласия -Пирсона (рис. 8).
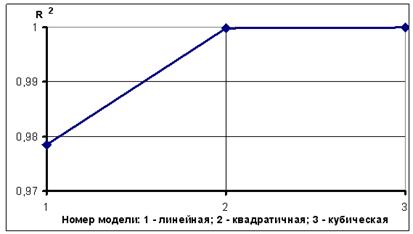
Рисунок 7. Изменение коэффициента детерминации при усложнении формы модели зависимости коэффициента а0 от параметра b
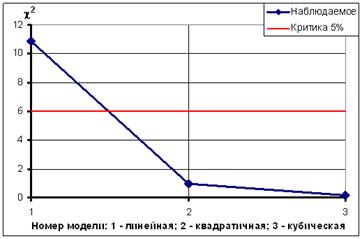
Рисунок 8. Динамика изменения наблюдаемого значения критерия согласия при усложнении модели
Таким образом, в результате данной работы построена модель зависимости среднего значения ФВМ от параметров функции:
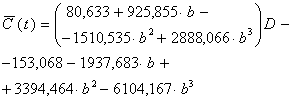
Причем, данная модель объясняет более 99,9% дисперсии корреляционных зависимостей рис.
СПИСОК ЛИТЕРАТУРЫ
- Седельников А.В., Бязина А.В., Антипов Н.Ю. Использование функции Вейерштрасса-Мандельброта для моделирования микроускорений на борту КА //Сборник научных трудов X Всероссийского научно-технического семинара по управлению движением и навигации ЛА. Самара. 2002. с. 124-128.
- Седельников А.В., Корунтяева С.С., Чернышева С.В. Анализ влияния параметров функции Вейерштрасса-Мандельброта на ее закон распределения //Современные наукоемкие технологии. - 2005 г. - № 9. - с. 43-46.
- Седельников А.В., Бязина А.В., Иванова С.А. Статистические исследования микроускорений при наличии слабого демпфирования колебаний упругих элементов КА //Научные чтения в Самарском филиале РАО. - Часть 1. Естествознание. - М.: Изд. УРАО. - 2003. - 137 - 158.
- Седельников А.В., Корунтяева С.С., Подлеснова Д.П. Исследование динамики изменения среднего значения фрактальной функции Вейерштрасса-Мандельброта как случайной величины //Фундаментальные исследования. - № 4. - 2006. - с. 84-87.
- Седельников А.В., Корунтяева С.С., Чернышева С.В. Выявление коридора значений параметров фрактальной функции Вейерштрасса-Мандельброта, при которых справедлив нормальный закон распределения функции //Современные наукоемкие технологии. - № 1. - 2006. - с. 85-87.