Рассмотрим в плоскости z полубесконечную область S. Функция
![]() , (1)
, (1)
где:
![]() комплексные числа,
комплексные числа, ![]() действительные числа, является частным случаем отображающей функции, приведенной в работе [1], при k=0. Она осуществляет конформное отображение нижней полуплоскости ImZ<0 на область S.
действительные числа, является частным случаем отображающей функции, приведенной в работе [1], при k=0. Она осуществляет конформное отображение нижней полуплоскости ImZ<0 на область S.
Пусть некоторый участок границы L области S, занимаемой упругим телом, получил смещение, причем, g1(t) и g2(t) - граничные значения компонент смещения. Необходимо определить напряженное состояние в области S.
Рассмотрим известное граничное условие, приведенное в работе [2]:
![]() , (2)
, (2)
где: ![]() и μ - упругие постоянные;
и μ - упругие постоянные; ![]() - граничные значения голоморфных в нижней полуплоскости функций
- граничные значения голоморфных в нижней полуплоскости функций ![]() , причем
, причем
![]() ,
,
где C - произвольная постоянная.
Будем считать, что при больших значениях | t | заданные функции подчинены условию
![]() ,
,
где G - произвольная комплексная постоянная.
Кроме того, полагаем, что ![]() удовлетворяет условию Гельдера, включая бесконечно удаленную точку.
удовлетворяет условию Гельдера, включая бесконечно удаленную точку.
Используя граничное условие (2), ему сопряженное и свойства интегралов типа Коши, получим
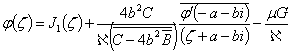 ; (3)
; (3)
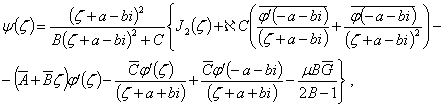 (4)
(4)
где
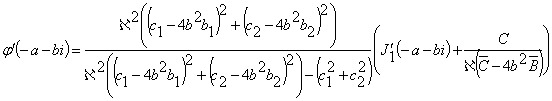 (5)
(5)
![]()
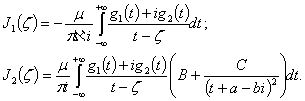 (6)
(6)
Для определения компонент напряжения необходимо воспользоваться формулами
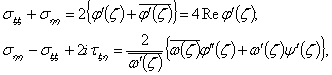 (7)
(7)
правые части которых могут быть вычислены при помощи формул (3) и (4).
После этого компоненты деформации определяются по формулам
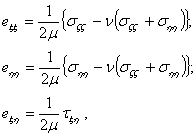 (8)
(8)
Рассмотрим пример.
Пусть отрезок ![]() оси
оси ![]() подвержен равномерному вертикальному смещению p, а остальная часть границы свободна от каких-либо внешних воздействий.
подвержен равномерному вертикальному смещению p, а остальная часть границы свободна от каких-либо внешних воздействий.
Отделив действительную часть от мнимой части в выражении (1), получаем при ![]() параметрические уравнения
параметрические уравнения
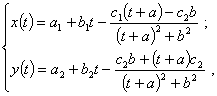 (9)
(9)
описывающие кривые, являющиеся границами односвязных областей, отображаемых функцией (1).
Итак, ![]() .
.
Формулы (3) и (4) при этом приобретают вид
![]() (10)
(10)
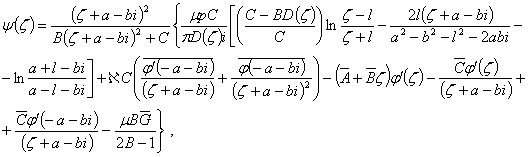 (11)
(11)
где: ![]() .
.
Условимся, что под выражением ![]() будем понимать приращение функции
будем понимать приращение функции ![]() при непрерывном изменении t в интервале
при непрерывном изменении t в интервале ![]() .
.
Подставляя выражения (1), (5), (6), (10), (11) в (7) и (8), получаем в замкнутом виде формулы для компонент напряжения ![]() и деформации
и деформации ![]() , дающие решение задачи для рассматриваемого случая.
, дающие решение задачи для рассматриваемого случая.
Полученные выражения при принятых выше условиях являются голоморфными в нижней полуплоскости функциями, поскольку этим свойством обладают функции, входящие в правую часть соотношения (7).
СПИСОК ЛИТЕРАТУРЫ:
- Богомолов А.Н. Расчет несущей способности оснований сооружений и устойчивости грунтовых массивов в упругопластической постановке / А.Н.Богомолов. - Пермь: ПГТУ, 1996.
- Мусхелишвили Н. И. Некоторые основные задачи математической теории упругости / Н.И.Мусхелишвили. - М.: Наука, 1966.



