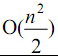Неуклонное расширение круга современных приложений при решении важных трудоемких задач по обработке многомерных сигналов звуковой локации, космической астрономии, сейсмографии, связи, медицинской электроники и другие проблемы требуют колоссальных объемов математических расчетов над большими массивами данных в реальном масштабе времени, выполнение которых невозможно без использования высокопроизводительных и надежных средств вычислительной техники. Все это ставит перед исследователями новые проблемы, связанные, прежде всего, с постоянным ужесточением требований к производительности и отказоустойчивости алгоритмических и аппаратных средств цифровой обработке сигналов (ЦОС). Одним из основных алгоритмов ЦОС является цифровая фильтрация, которая может быть реализована с помощью вычисления свертки, с помощью алгоритмов дискретного преобразования Фурье, алгоритма Винограда преобразования Фурье, теоретико-числового преобразования, а также их различных модификаций и быстрых реализаций. Помимо алгоритмов, использующих частотное представление сигнала, широко используются алгоритмы, работающие в пространственных координатах, такие как линейные и нелинейные преобразования и алгоритмы, основанные на изучении статистической модели шума. Однако следует заметить, что не всегда удается решить обратную задачу, т.е. отделить полезный сигнал от шумовой составляющей. Применение статистических алгоритмов осложняется необходимостью построения точной модели шума для конкретного случая, что тоже удается сделать далеко не всегда.
В данной работе предлагается использовать интегральное преобразование сигнала для получения его энергетической характеристики, с последующей трансформацией сигнала в зону понижения шумов.
Суть метода заключается в анализе сигнала с точки зрения распределения его энергии по всевозможным областям, на которых определен сигнал. Для данного анализа на координатной сетке строиться гиперповерхность. Точка на координатной сетке определяет область сигнала, а значение гиперповерхности в данной точке определяет энергию сигнала, содержащуюся в соответствующей области сигнала.
Процедура восстановления исходного сигнала из гиперповерхности является нелинейной фильтрацией, и основана на трансформации сигнала в точки с наибольшей энергией. Экспериментально подтверждено, что данная трансформация фильтрует сигнал от импульсной и аддитивной шумовых составляющих значительно лучше, чем наиболее распространенные на сегодняшний день методы фильтрации, такие как метод скользящего окна, метод медианной фильтрации и др. [1].
Однако алгоритм метод оптимального среднего является крайне тяжелым алгоритмом с точки зрения вычислительной сложности, к тому же, циклы данного алгоритма не могут быть параллельно выполнены на многопроцессорном вычислительном комплексе, из-за сцепления по переменным в телах циклов. В связи с чем, был проведен анализ его вычислительного ядра. Результатом данного анализа явилась модифицированная версия алгоритма с меньшей вычислительной сложностью, а также параллельной структурой. Модифицированный алгоритм лишен сцепления по переменным между внутренними вычислительными циклами, что позволяет эффективно выполнять программу, реализующую данный алгоритм, в среде вычислительного кластера с помощью технологий MPI или OpenMP.
Таблица 1. Сравнительная характеристика исходного и модифицированного алгоритмов
|
Алгоритм |
Вычислительная сложность |
Размерность простантства итераций |
Возможность параллельного исполнения циклов |
Возможность параллельного исполнения инструкций внутри циклов |
|
Исходный |
|
3 |
Нет (по всем измерениям) |
Нет (по всем измерениям) |
|
модифицированный |
O (n) |
2 |
Да (по всем измерениям) |
Да (по всем измерениям) |
СПИСОК ЛИТЕРАТУРЫ:
- Мезенцева О.С. Андреев А.А. Сравнительный анализ методов фильтрации шума в дискретных сигналах // НТЖ «Автоматизация, телемеханизация и связь в нефтяной промышленности». - М.: 2007. -№2. - с.22-28.