В современных педагогических исследованиях широко используется системный подход, в котором в качестве субстанции приняты понятия: «педагогическая система», которая описывает структуру, связи, организацию объекта; «педагогический процесс», который описывает - что происходит в исследуемом, а «педагогическая технология» - как это происходит (Г.Н. Александров и др.).
Преследуя цель повышения качества подготовки специалистов, следует активно осуществлять управление педагогическим процессом получения и освоения знаний студентами. Универсальной характеристикой педагогического процесса является педагогическое взаимодействие. В последние годы в связи с достижениями психологии общения акцент смещается на проектирование способов учебного диалога: диалог между преподавателем и студентом, студентов друг с другом, группы студентов и преподавателя. Диалог призван улучшать усвоение учебного материала, влиять на мотивационную сферу познавательной деятельности студентов и, следовательно, на контрольно-оценочную сферу.
Особую роль в познании играет когнитивная психология, которая исследует познавательные процессы приема, сохранения, переработки, воспроизведения и использования информации (Р.Солсо). Организация познавательной деятельности студентов принадлежит преподавателю. Педагогические задачи могут быть решены и решаются посредством повышения активности студентов только под его руководством. Психологические исследования свидетельствуют, что лишь на треть процесс обучения обусловлен способностями обучаемого, а на остальные две трети - его эмоциональным состоянием. Продуктивное эмоциональное состояние интериоризации студентов должен создать преподаватель. Существуют разные методы. Одним из действенных является проблемное обучение. Психологические, методологические, дидактические основания проблемного обучения проанализированы В.И. Идиатулиным.
Для оценки результатов обучения студентов с 2003 года в ТулГУ используется балльно-рейтинговая система по всем дисциплинам учебных планов всех форм профессионального высшего образования. Эта система предполагает проведение мероприятий текущей и промежуточной аттестации, и она не только способствует повышению внешней мотивации студентов к систематическому, успешному усвоению дисциплин, но и выявляет качества предлагаемых образовательных услуг, их соответствие (и несоответствие) международным стандартам и обнаруживает степень эффективности педагогического процесса.
Можно предположить, что высокий уровень знаний студентов совпадает с высокой долей контактов преподавателя со студентами, инициированных самим преподавателем, владеющим приемами формирования различных структур интеллектуальных процессов (алгоритмических, полуалгоритмических, полуэвристических, эвристических) (Л.Н.Ланда, К. Банг) и иными основами проблемного обучения. В этом случае для описания учебного процесса можно воспользоваться описанием случайных процессов, протекающих в системе массового обслуживания. Случайный процесс, протекающий в системе массового обслуживания, состоит в том, что система в случайные моменты времени переходит из одного состояния в другое. Учебное занятие рассматривается как случайный процесс с непрерывным временем. Переход системы из одного состояния в другое осуществляется скачком, в момент, когда осуществляется какое-либо событие (в данном случае - коммуникация между студентом и преподавателем). Например, дискретная система X, где различные состояния системы соответствуют различному числу коммуникаций: X0- ни одной коммуникации, X1 - одна коммуникация; Xk - k коммуникаций; Xn - все n участвовали в коммуникативном общении. Для такой системы характерны необратимые переходы. Упрощенно можно представить каждый этап учебного занятия как поток однородных событий (заявок на обслуживание) и описать его свойства с помощью теории массового обслуживания как стационарный пуассоновский поток [1].
На произвольном участке времени длиной 
число событий, попадающих на данный временной участок, распределено по закону Пуассона с математическим ожиданием
, (1)
где λ - плотность потока, (среднее число коммуникаций между преподавателем и студентом, приходящееся на единицу времени)
Вероятность того, что за время произойдет ровно m событий, равна
(2).
Для данной системы можно записать закон распределения с заданной плотностью
при 
(3).
При рассмотрении практических и семинарских занятий можно предположить, что поток событий не стационарен из-за возможных усложнений коммуникаций (возникших дискуссий, постановки новых проблем). Мгновенная плотность потока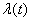 
на временном участке 
, (4)
где m(t) - математическое ожидание числа событий на участке (0,t). Число событий, попадающих на участок длины
,(5),
где 
- математическое ожидание числа событий на участке от t0 до 
, равное
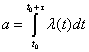(6).
Закон распределение будет иметь вид:
(7).
Педагогический эксперимент и анализ данной модели проводили в ТулГУ на кафедре «Физика» естественнонаучного факультета по дисциплинам «физика» в группах инженерных специальностей, а также на кафедре «Мировая экономика и право» экономического факультета по дисциплинам: «Правовое регулирование внешней экономической деятельности предприятий» и «Таможенное и валютное регулирование».
Заключение: Предлагаемая модель в качестве вероятностного описательного средства универсальна, и ее можно адаптировать к условиям каждой конкретной дисциплины и формы обучения. Данная модель позволяет лучше постичь наблюдаемое в педагогическом процессе, а именно увидеть корреляцию между результатами оценок знаний по балльно-рейтинговой системе и применением рациональных педагогических действий проблемного обучения.
СПИСОК ЛИТЕРАТУРЫ:
- Вентцель Т.Е. Теория вероятностей: Учеб. Для вузов. - 7-е изд. стер. - М.: Высш. шк., 2001 - 575с: ил.
- Горбунова О.Ю. Лахатова М.И. Повышение эффективности учебного процесса на примере физического практикума с учетом педагогического взаимодействии «преподаватель-студент» «Физика в системе инженерного образования стран ЕврАзЭС» и совещания заведующих кафедрами физики технических ВУЗов России, стр. 83- 85 М, 2007.