Известные математические модели процессов воспламенения и горения реагирующих сред основаны на рассмотрении сопряженных теплофизических и термокинетических явлений в пограничном слое. При этом, основными механизмами реализации данных процессов являются составляющие конвективного и диффузионного переноса тепловой энергии (энтальпии) в среде с учетом неравновесных источников внутреннего тепловыделения и химической кинетики. Уточнение физической сущности процессов теплопроводности и химической кинетики, определяющих явления воспламенения и горения реагирующих конденсированных сред (РКС), представляется одним из наиболее сложных разделов аналитической и вычислительной тепломеханики и термохимии.
Предложен дивергентный вид системы одномерных дифференциальных уравнений в частных производных, определяющих характеристики процессов теплопереноса и химической кинетики n-го порядка в пограничном слое РКС:
![]() (1)
(1)
где A(x,t), B(x,t), C(x,t) - векторы-столбцы искомых функций состояния, составляющих переноса и активности внутренних источников.
Ω (x,t) - функция скорости реакции в источнике (кинетический множитель Аррениуса).
В основе существующих математических схем и аппроксимаций системы уравнений (1) положены различные варианты метода конечных разностей: алгоритмов явной схемы «предиктор-корректор», явной схемы Адамса - Бэшфорта и неявной итерационной схемы.
В результате проведенного анализа особенностей получаемых решений было выявлено, что явные схемы не обеспечивают необходимой устойчивости решения в окрестности точки перехода от режима инертного прогрева к воспламенению, что частично устраняется введением дополнительных сглаживающих процедур и значительным снижением шага интегрирования. Для реализаций неявных схем, данное сглаживание является избыточным (проявляются известные диффузионные свойства неявных аппроксимаций), что также негативно сказывается на точности получаемых решений.
Предложена схема вычислительного решения системы неоднородных уравнений (1), использующая метод расщепления. Вычислительный цикл схемы включает три последовательно выполняемых этапа внутри единичного шага по времени.
1. На данном этапе изменяются величины Tin и βin , относящиеся непосредственно к i-ой ячейке - составляющих компонентов векторов А и С (1), без учета потоков конвективного и диффузионного переноса. Внутреннее тепловое состояние ячейки является замороженным:
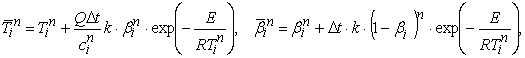 (2)
(2)
2. На данном этапе проводится вычисление эффектов переноса - составляющих компонентов вектора B (1), учитывающих обмен между ячейками (i; i+1) и (i-1; i):
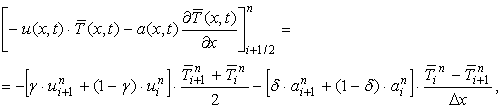 (3)
(3)
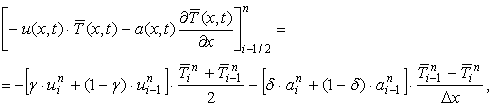
![]() (4)
(4)
![]()
где ![]()
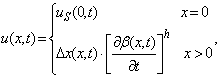
3. Здесь происходит перераспределение тепловой энергии в пространстве реагирующей среды в момент времени tn+1. На новом временном слое, исходные уравнения аппроксимируются следующим образом:
![]() (5)
(5)
Компоненты векторов В и С определяются с учетом решений первого этапа (2).
Проведены исследования и показана сходимость схемы решения (2-5) уравнений (1) для широкого диапазона краевых условий процессов воспламенения и горения РКС.



