Представляет интерес исследование возвратно-поступательных колебаний характерных для демпферов возвратно-поступательного движения, когда непрерывно изменяются во времени частоты и скорости движения.
Для упрощения анализа исследования, используя общепринятые допущения [1], пренебрегаем продольным краевым эффектом. В системе координат, расположенной на индукторе, первичное поле не меняется во времени и 
. Напряженность магнитного поля имеет одну составляющую по оси Z. Принятая конструкция демпфера такова, что движение возможно только вдоль оси X. При дальнейшем анализе электромагнитных процессов принимаем скорость движения вторичного элемента по периодическому закону
,
где 
- среднее значение скорости; 
- заданная периодическая функция.
При этом вектор скорости имеет только одну пространственную составляющую, которая изменяется по гармоническому закону
,
где 
- максимальная скорость подвижной вторичной среды; xm - амплитуда колебаний; ω2 - частота колебаний вторичной среды.
Тогда 
, так как в этом случае 
и 
.
При этом амплитуда и частота колебаний неизменны, а вторичный элемент движется по гармоническому закону
,
где X - координата, определяющая положение вторичного элемента;
Принятая форма записи координат и скорости соответствует тому, что в начальный момент времени подвижный вторичный элемент находился в положении равновесия и мгновенно получил максимальную скорость, например, в результате удара.
Так как первичное магнитное поле в зазоре изменяется по гармоническому закону по оси , то все вторичные электромагнитные величины также изменяются по гармоническому закону т.е.
,
где 
- амплитуда индукции вторичного магнитных полей.
Тогда получим 
.
При этом целесообразно перейти к относительным единицам, используя следующие соотношения 
; 
; 
; 
; 
.
Следовательно,
, (1)
где 
- магнитное число Рейнольдса или безразмерная средняя скорость (частота) движения; 
- средняя частота движения (вращения); 
- частота движения, выраженная в долях частоты колебаний. Также можно показать, что 
, где 
- безразмерная амплитуда колебаний.
Обычно краевые эффекты незначительны при 
и, кроме того, поперечные прорези во вторичной среде также уменьшают их влияние. Поэтому дополнительно можно принять допущение о том, что длина сплошного вторичного элемента по оси y бесконечна, и краевые явления отсутствуют. Тогда
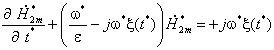. (2)
В начальный момент вторичное магнитное поле отсутствует, т.е. 
. Тогда решение (2) может быть найдено в следующем виде
,
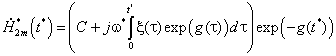где C - постоянная интегрирования, определяемая начальными условиями:
.
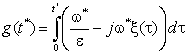В случае, если скорость изменяется по гармоническому закону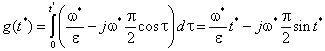 
решение (2) тогда может быть найдено в следующем виде
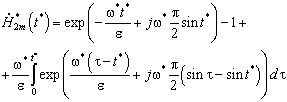. (3)
За период напряженность поля изменяется дважды. Смена направления не сказывается на величине поля, однако при смене направления происходит существенное снижение поля вихревых токов, которое постепенно нарастает до значения поля в режиме линейного перемещения. При больших значениях безразмерной частоты , поле достигает этого значения лишь непосредственно к моменту последующей смены направления движения, что связано с увеличением постоянной времени. Таким образом, при изменении направления движения изменяют направление индуктируемые вихревые токи, однако вследствие инерционности процесса, поле не равно максимальному значению во время полупериода движения. Смена направления тока происходит не в момент изменения направления скорости, а несколько позже. При больших частотах 
изменение тока во времени близко к гармоническому закону.
Проведенные расчеты позволяют сделать вывод, что при уменьшении 
(увеличении 
) переходной процесс занимает относительно меньшее время и поле равно максимальному значению практически весь полупериод, а тормозная электромагнитная сила увеличивается и приближается к предельному значению.
СПИСОК ЛИТЕРАТУРЫ
- Исмагилов Ф.Р. Электромагнитные элементы систем управления со сложной геометрией ротора - Уфа: УГАТУ, 1997. - 139 с