Пусть y(t) - интенсивность выпуска продукции некоторого предприятия. Предположим, что весь выпущенный предприятием товар будет продан, а также цену товара p(y) будем считать убывающей функцией. Чтобы увеличить интенсивность выпуска y(t), необходимо, чтобы чистые инвестиции I(t) были больше нуля. Таким образом, скорость увеличения интенсивности выпуска продукции является возрастающей функцией от I. Пусть эта зависимость выражается прямой пропорциональностью.
(1)
где 
-норма акселерации. Пусть λ - норма чистых инвестиций, т.е. часть дохода p(y)•y, которая тратится на чистые инвестиции, тогда 
.
Уравнение (1) запишется 
, где 
.
Примем 
, где 
. Тогда 
. (2)
Рассмотрим ситуацию, когда два предприятия выпускают один и тот же товар. Динамика объемов, выпускаемого товара каждым предприятием, определяется следующей системой
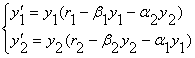(3)
Здесь yi - количество, выпускаемого товара i - ым предприятием, ri - коэффициент прироста выпускаемого товара i - ым предприятием, βi - коэффициент, описывающий влияние на интенсивность выпуска продукции в самом предприятии, αi - коэффициент, описывающий влияние со стороны другого предприятия. Все коэффициенты положительны. Из уравнений (3) следует, что система имеет следующие особые точки
1. y1=0, y2=0, 2. y1=0, 
,
3. 
, y2=0, 4. 
, 
.
Исследуя систему можно сделать вывод, что при определенных условиях, если в системе в начальный момент времени существовали оба предприятия, то при любом соотношении их интенсивностей с течением времени второе предприятие полностью разорится и останется только первое со стационарным объемом 
.
В зависимости от соотношения начальных объемов в системе выживает одно из предприятий. Ситуация, когда в системе сосуществуют оба предприятия с постоянными интенсивностями, является теоретически возможной, но практически крайне маловероятной.
При различных соотношениях параметров, если особая точка 4 - устойчивый узел, а особые точки 2,3 - седла, то в системе устанавливается устойчивое стационарное состояние, при котором оба предприятия сосуществуют.