Сложное эндогенное и экзогенное взаимодействие индикаторов в прогнозируемых экономических процессах диктует необходимость привлечь к их исследованию системный анализ, теорию функций, статистику, эконометрику, прогностику, дискретную математику с аппроксимацией (интерполяцией и экстраполяцией) решетчатых функций, моделирующих динамику экономических показателей.
В современной прогностике недостаточное внимание обращалось на гибкие технологии прогнозирования экономических процессов, меняющих класс своего временного поведения на отчетном участке при смене экономического законодательства. Классическое детерминированное прогнозирование с подбором наиболее релевантного (экономическому процессу) многочлена или группы многочленов (комбинированная модель) должно быть дополнено универсальным аппаратом прогнозирования с казалось бы противоречивыми свойствами (низкая степень, высокая точность, необходимость "сшивки" фрагментов), что расширяет круг моделируемых и прогнозируемых процессов.
В известных прогнозирующих моделях не всегда явно прописываются и используются внутренние оптимизационные свойства аппроксимирующих многочленов и реализующего их аппарата, нужные для переноса статистических особенностей процесса из отчетного периода в прогнозируемый горизонт. Свойство минимальной нормы сплайнов лучше сохраняет статистику и строит более точный прогноз.
Регрессионные построения на системах решетчатых функций вынуждали использовать (из критериев согласия) только метод наименьших квадратов. Замена решетчатых функций сплайнами (и их производными) дает в руки экономиста весь спектр математических методов. Невысокий порядок составляющих сплайна облегчает экономическую интерпретацию и управление ими.
В классических методах прогноза много хлопот доставляет "стык" между отчетным и перспективным периодами. Сплайны хорошо реализуют "сшивку" функций и ее производных в таких "стыках".
Известные методы прогнозирования не всегда отличались универсальностью, где-то оказывались громоздкими, что затрудняло экономисту работу с ними. Предлагаемый подход конструктивен, универсален и прост, поддержан возможностями системы аналитических вычислений MAPLE 6, возможна реализация на персональных компьютерах.
В классификации технологий прогнозирования выделяются три подхода к формальному (детерминированному) прогнозированию. Поскольку экономический процесс представлен решетчатой функцией, по виду которой трудно определить его характер, а временной класс процесса заранее неизвестен исследованию, то первый подход базируется на переборе альтернативных систем функций: назначается та система функций, тот полином, который лучше других количественно интерполирует (а затем и экстраполирует) процесс.
Во втором подходе процесс 
последовательно и аддитивно уточняется различными моделями, в этом алгоритме могут меняться как классы приближающих функций, так и критерии согласия. Остаток от применения первой модели 
рассматривается как новый процесс:
.
Он интерполируется и экстраполируется второй моделью 
с возможностью изменения и целевой функции:
и т.д. до
...
Тогда комбинированная модель, более точно представляющая процесс,
...
В новом третьем подходе полагается, что класс экономического процесса может изменяться во времени, это связывается с изменением законодательства, затрагивающим экономическую составляющую жизни общества (изменением таможенных тарифов, правил и размеров налогообложения и пр.). Для получения более точного прогноза с большим периодом упреждения отчетный период необходимо иметь как можно более долгим. А это уже гарантирует, что процесс на протяжении отчетного времени будет претерпевать несколько этапов указанных изменений, которые либо ускоряют (замедляют) ход процесса, изменяя только его параметры, либо вообще меняют временной класс
Предлагается кусочно-полиномиальный подход к прогнозированию экономических показателей. В связи с принципиальным выбором в исследовании третьего подхода утверждается, что какой то один класс аппроксимирующих функции не может достаточно просто и точно моделировать и прогнозировать экономический, производственный, финансовый, маркетинговый процесс, когда класс процесса меняется на протяжении отчётного периода. Поэтому приводятся соображения о полезности в моделировании и прогнозировании "кусочно-полиномиальных" подходов. Успех такого представления в детерминированной прогностике связан с необходимостью построения прогнозного фрагмента в перспективном периоде так, чтобы он был плавно связан с последним фрагментом отчётного периода в точке 
при перспективном прогнозировании (и с начальным фрагментом в точке 
при ретроспективном прогнозировании).
Найдено, что модель, лучше всего соответствующая процессу, становится «кусочно-релевантной», на разных отрезках 
отчётного периода она может представлять разные классы экономического поведения, это заставляет нас искать решение в кусочно-полиномиальной аппроксимации, использовать приближение кусочно-полиномиальными функциями (многозвенниками). Необходимой составной частью такого подхода является "сшивка" кусков аппроксимирующей функции в единый ансамбль в узловых точках 
. "Сшивка" осуществляется значениями самой функции 
и значениями её производных 
, 
и т.д. слева и справа в каждой узловой точке, так что 
, 
, 
и пр. становятся непрерывными функциями во всём интервале 
. Из всех кусочно-полиномиальных функций мы остановили свой выбор на сплайн-функциях.
Отличительная особенность сплайн-функций (сплайнов) - они состоят из отрезков степенного полинома малого порядка (степени), которые сходятся в заданных узловых точках процесса (узлах решётчатой функции). Математический сплайн n-го порядка (степени) непрерывен и имеет (n - 1) непрерывную производную, n-я производная может претерпевать в точках соединения разрыв с конечным скачком. Такая структура сплайна позволяет автоматически "сшить" решение в единый комплекс, используя при этом наличие у сплайнов полезного внутреннего свойства - свойства минимальной кривизны.
При обзоре теории сплайн-функций можно выделить их конструктивную единицау- "момент". "Моменты" Mj находятся из матричного равенства 
. В прогнозировании экономического поведения статистика «моментов» в отчётном периоде позволяет следить за ускорением экономического процесса, более глубинной его характеристикой. Удается вычислить прогнозирующий «момент» на перспективном интервале, который после построения всего сплайна «проявляется» в значении прогнозирующей функции в точке Xz.
Выделяется то свойство сплайнов, которое при поиске классов подходящих полиномов мы называем "внутренней оптимальностью". У кубических сплайн-функций SA(Y;X) оно выражается теоремой Холлидея, в которой показано, что сплайн-построение минимизирует интеграл:
.
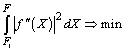Это свойство кубического сплайна называется свойством наилучшего приближения, минимальной кривизны или минимальной нормы. Оно соответствует минимуму потенциальной энергии, затраченной на отклонение балки в "механических сплайнах". Кубические сплайны непрерывны сами и непрерывны их первые производные. Вторые производные непрерывны и кусочно-линейны. Третьи производные разрывны с конечным скачком.
Сплайн прогнозирование базируется на следующей идее (в качестве примера рассмотрим проспекцию):
"предыдущий" участок сплайна заканчивается в последней узловой точке процесса , последняя узловая точка представляет значение экономического показателя YN в момент времени XN ("сегодня") на правой границе отчётного периода;
"последующий" (вправо) участок сплайна опирается на значение YN, последний "момент" вычисляется по статистическому распределению "моментов" внутри отчётного периода, сплайн с этим "моментом" на последнем отрезке и становится экстраполирующим, он продолжается от XN до XZ;
"предыдущий" и "последующий" отрезки "сшиваются" в точке значениями моделирующей процесс сплайн-функции слева и справа и всеми ее производными до (n - 1)-ой включительно.
В настоящее время принято прогнозирование одного и того же экономического показателя осуществлять различными приёмами - для повышения точности расчётов. Организуется этот процесс с помощью прогнозирующих систем.
Прогнозирующие системы определяются как совокупность методов, приемов и процедур, позволяющих получать прогнозы при заданной целевой функции развития объекта прогнозирования, при заданном объёме прогнозной информации. Прогнозирующие системы выполняют две основные операции: формируют множество альтернатив, обликов объектов прогнозирования; сравнивают и выбирают альтернативы. Объединение этих операций определяет комплексную проблему системного прогнозирования, средством решения которой и является прогнозирующая система. В прогнозирующих системах реализуются следующие основные принципы: взаимоувязанность и соподчинённость прогнозов различных уровней иерархии объекта прогнозирования, внешнего окружения, различных аспектов исследования объекта прогнозирования; согласованность нормативных и исследовательских прогнозов; непрерывность прогнозирования, корректирующая прогнозы по мере поступления новой информации.