Одно из центральных мест в современной теории апериодического состояния занимает вопрос о связи квазикристаллического и кристаллического порядков и их взаимопревращениях. Общепринято, что фазовый переход квазикристалл (КК) - кристалл (К) обусловлен нестабильностью фазонной подсистемы КК относительно линейных фазонных деформаций [1]. Описание развития такой неустойчивости КК в том или ином приближении не вызывает трудностей и хорошо исследовано. Но открытым остается вопрос о стабилизации ("замораживании") конкретной фазонной деформации, соответствующей кристаллическому состоянию. Полученные нами результаты показали, что для чисто кристаллических фазовых переходов стабилизация аналогичных деформаций имеет симметрийную природу [2]. Собственная симметрия рассматриваемого механизма фазового перехода приводит к такому виду потенциала взаимодействия фононной и структурной подсистем, что выделенные линейные фононные искажения стабилизируются как отдельные фазовые состояние. Целью настоящей работы является исследования собственной симметрии линейных фазонных и фононных деформаций и ее влияния на стабилизацию КК и К состояний.
Рассмотрим плоскую двумерную квазикристаллическую структуру, относящуюся к полигональной симметрии. Исследуем для этой структуры искажения, обусловленные линейными фазонной и фононной деформациями. Параметр порядка (ПП) в этом случае реализуется на базисных волновых векторах b1, b2, b3 и b4, т.е. восьмимерный.
Для квазипериодических объектов такие базисы образуют всюду плотный модуль, причем один и тот же модуль может быть описан различными эквивалентными базисными векторами. Из теории линейных уравнений следует, что базисные векторы являются эквивалентными, если они переводятся друг в друга унимодулярной матрицей (матрицей с любыми целочисленными коэффициентами и определителем, равным по модулю единице) [2]. Таким образом, группой собственной симметрии структурных искажений, связанных с линейными фазонной и фононной деформациями, является унимодулярная группа, действующей на пространстве базисных векторов, т.е. в пространстве параметра порядка.
Для построения базиса инвариантов этой группы возьмем расширенный набор генератора:
![]() (1)
(1)
где S и T - двумерные матрицы, образующие для двумерной унимодулярной группы [2]; E - двумерная единичная матрица.
Первые два элемента являются генераторами подгруппы унимодулярных преобразований двумерного подпространства, образованного базисными векторами b1, b2. Как показано в [2], целый рациональный базис (ЦРБИ) для нее состоит из двух комплексных модулярных форм g2(b1, b2) и g3(b1, b2):
J1= g2(b1, b2); J2= g3(b1, b2) (2)
Аналогичным образом, для второй пары генераторов (1) ЦРБИ будет:
J3= g2(b3, b4); J4= g3(b3, b4) (3)
Последний элемент (1) образует подгруппу второго порядка перестановок подпространств (b1, b2) и (b3, b4). Легко видеть, что ЦРБИ представления этой подгруппы, построенного на функциях (2) и (3), будет также базисом инвариантов для группы (1):
V1=J1+J3; V2=J2+J4; V4=(J1-J3)2;
V5=(J2-J4)2; V4=(J1-J3) (J2-J4) (4)
Отметим, что термодинамический потенциал должен быть инвариантным относительно поворота всей плоскости как единого целого на произвольный угол (группа C∞). Строя на (4) представления группы C∞ и определяя базис инвариантов этих представлений, получим ЦРБИ группы G0 собственной симметрии рассматриваемого механизма структурных искажений:
Ik=Re(ViVj*) (5)
где * - знак комплексного сопряжения; i, j пробегают значения от 1 до 5, причем i меньше или равно j.
В (5) входят 15 инвариантов и типичный термодинамический потенциал является версальной деформацией положительно определенной квадратичной формы от этих инвариантов:
F = ΣαiIi + ΣβikIiIk (6)
где αi, βik - феноменологические коэффициенты.
Вышеприведенная методика построения базиса инвариантов группы G0 основана на разложении этой группы в нормальный ряд [3]:
G2 ⊂ G1 ⊂ G0 (7)
где G2 - унимодулярная группа, действующая на двумерном подпространстве (b1, b2); фактор - группа G1/G2 изоморфна группе второго порядка перестановок подпространств (b1, b2) и (b3, b4); фактор - группа G0/G1 изоморфна группе поворотов комплексного пространства на любой угол C∞. Как показано в современной теории фазовых переходов [3], отдельно выделенные фазы соответствуют подпространствам ПП, инвариантным относительно какой-либо нормальной подгруппы. Для симметрийной классификации таких фаз достаточно перечислить с точностью до внутреннего автоморфизма все инвариантные подпространства.
Группа G2 действует инвариантным образом на подпространстве b1||b2, соответствующем решению уравнений состояний (отдельной апериодической фазе) типа (b1||b2, b3 и b4 любые). Из этого подпространства можно выделить более узкое подпространство (b1||b2, b1=b3, b2=b4), инвариантное относительно группы G1, образованной G2 и фактор - группой G1/G2. Это инвариантное подпространство соответствует состоянию, имеющем апериодический порядок только в одном направлении (типа жидкого квазикристалла).
Используя нормальные подгруппы группы G2 и ряд вложений (7), можно получить другие инвариантные подпространства и определить тип соответствующих им фаз. В [2] нами показано, что двумерная унимодулярная группа имеет пять инвариантных подгрупп, которые выделяют на пространстве (b1, b2) фазы, соответствующие всем двумерным кристаллическим классам. Эти подгруппы на пространстве (b1,b2,b3,b4) будут выделять инвариантные подпространства, соответствующие апериодическим фазам №3 - №7, приведенным в таблице 1.
Таблица 1. Симметрийная классификация решений уравнений состояния типичного термодинамического потенциала (11)
|
№ |
Соотношения между компонентами ПП |
Инвариантная подгруппа |
Примечан. |
|
|
Подпространство (b1, b2) |
Подпространство (b3, b4) |
|||
|
1 |
b1 | | b2 |
Моноклинная система |
G2 |
Апериодич. состояние |
|
2 |
b1 | | b2 |
b1 = b3, b2= b4 |
G1 |
Жидкий КК |
|
3 |
Моноклинная система |
Моноклинная система |
G20 =E |
Апериодич. состояние |
|
4, 5 |
Орторомбическая (гц. орторомбическая) система |
Моноклинная система |
G21 (G22) |
Апериодич. состояние |
|
6, 7 |
Тетрагональная (гексагональная) система |
Моноклинная система |
G23 (G24) |
Апериодич. состояние |
|
8 -12 |
Соответствуют № 3 - № 8, 2 ст. |
b1 = b3, b2= b4 |
G2i• G1/G2 |
Кристалич. состояния |
|
13 -22 |
Различные сочетания подпространств (3 - 7, ст.2) и (3 - 7, ст.3) |
G2i |
Апериодич. состояния |
|
|
23 |
|b1|=|b2|,
|
|b3|=|b4|,
|
G22 G32•C5 |
Декагональный КК |
|
24 |
|b1|= |b2|,
|
|b3|= |b4|, |
G23 G33•C8 |
Октагональный КК |
|
25 |
|b1|= |b2|,
|
|b3|=|b4|,
|
G22 G32•C12 |
Додекагональный КК |
Из этих подпространств можно выделить более узкие подпространства (b1 = b3, b2 = b4), инвариантные относительно групп G1i, образованных G2i и фактор - группой G1/G2. Такие подпространства соответствуют чисто кристаллическим фазам (см. № 7 - №12, Табл.1).
Рассмотрим группу G3, сопряженную группе G2 и действующую на подпространстве (b3, b4). Ее нормальные подгруппы выделяют инвариантные подпространства, аналогичные (3 - 7, ст.2, Табл.1) и соответствующие доменам фаз № 3 - № 7. Однако группы G2iÄG3i, являющиеся прямым произведением нормальных подгрупп группы G2 и группы G3, выделяют инвариантные подпространства, соответствующие другим фазам. Такие инвариантные подпространства легко получить перебирая все возможные сочетания подпространств (3 - 7, ст.2) Табл.1 и (3 - 7, ст.3) Табл.1. С учетом внутренних автоморфизмов будет 10 различных сочетаний, соответствующих 10 апериодическим фазам. Из этих фаз наибольший интерес представляют три, имеющих симметрию G23![]() G33 (|b1|= |b2|,
G33 (|b1|= |b2|, 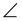 b1 b2=π/2, |b3|= |b4|,
b1 b2=π/2, |b3|= |b4|, 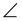 b3 b4=π/2), G23
b3 b4=π/2), G23![]() G33 (|b1|= |b2|,
G33 (|b1|= |b2|, 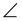 b1 b2=2π/3, |b3|= |b4|,
b1 b2=2π/3, |b3|= |b4|, 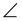 b3 b4=2π/3) и G22
b3 b4=2π/3) и G22![]() G32 (|b1|= |b2|, |b3|= |b4|). Подгруппа С8 фактор группы G0/G1 выделяет из инвариантного пространства симметрии G23
G32 (|b1|= |b2|, |b3|= |b4|). Подгруппа С8 фактор группы G0/G1 выделяет из инвариантного пространства симметрии G23![]() G33 инвариантное подпространство, соответствующее октагональной квазикристаллической фазе. Аналогичным образом, подгруппы С12 и C5 выделяют из G24
G33 инвариантное подпространство, соответствующее октагональной квазикристаллической фазе. Аналогичным образом, подгруппы С12 и C5 выделяют из G24![]() G34 и G22
G34 и G22![]() G32 инвариантные подпространства, соответствующие додекагональной и декагональной квазикристаллическим фазам.
G32 инвариантные подпространства, соответствующие додекагональной и декагональной квазикристаллическим фазам.
Таким образом, для рассматриваемого механизма фазовых превращений в планарных КК - линейных фазонных и фононных деформациях - на фазовых диаграммах должны существовать области стабильности, соответствующие всем полигональным КК состояниям и области стабильности для периодических структур всех кристаллических классов. Кроме того, на фазовых диаграммах должны наблюдаться промежуточные апериодические состояния (имеющие более низкую точечную симметрию), все возможные типы которых приведены в таблице 1. Стабилизация всех приведенных в таблице выделенных линейных фазонных и фононных деформаций как индивидуальных фаз обусловлена их собственной симметрией. Описание фазовых переходов между этими структурами возможно на основе единого ПП, реализующегося на четырех базисных волновых векторах.
Работа выполнена при поддержки РФФИ, грант № 02-02-17871.
ЛИТЕРАТУРА
- Show L.J., Elser V., Henley C.L. // Phys. Rev. B. 1991. V.43. P.3423.
- Мощенко И.Н., Винберг Э.Б., Гуфан Ю.М. //Известия высших учебных заведений. Северо - Кавказский регион. Естественные науки. 2003. № 3. С.12
- Гуфан Ю.М. Структурные фазовые переходы. М.: Наука, 1982. 304 с.



