Библиография работ, посвященных поверхностным волнам в жидких средах, взаимодействующих с электрическим полем, весьма обширна. В связи с этим здесь не представляется возможным привести сколько-нибудь подробный обзор этих работ. Впервые задача о распространении гравитационных электрокапиллярных волн на поверхности жидкого проводника (в линейном по амплитуде приближении) была решена, по-видимому, Я.И. Френкелем [3]. Авторы последующих работ по этой теме ограничивались линейным приближением. Лишь сравнительно недавно появились публикации, в которых при помощи методов возмущений [6] учитываются более высокие приближения. Так, например, в [2] в задаче об электрокапиллярных волнах на поверхности идеальной жидкости учитываются первые два приближения по амплитуде волны. Однако рассматриваемый нами анализ задачи с точностью до первых трех приближений позволяет более точно описать явление и объяснить новые эффекты.
Рассматривается распространение бегущих волн по заряженной поверхности бесконечно глубокого слоя жидкого проводника в поле тяжести. Несжимаемая и однородная жидкость граничит со средой пренебрежимо малой плотности (газ, вакуум).
Систему уравнений движения запишем в виде [3,4]
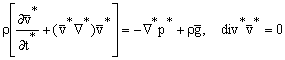; (1)
, 
(
),
, 
,
где 
- плотность, 
- скорость,p* - давление, 
- ускорение свободного падения, 
- напряженность электрического поля, φ*- электрический потенциал, ε - диэлектрическая проницаемость. Звездочкой здесь и далее обозначены (в необходимых случаях) размерные величины, чтобы отличать их от безразмерных, обозначенных теми же буквами без звездочек. Отметим, что электрическое поле имеется лишь вне жидкого проводника.
Невозмущенная поверхность жидкости совпадает с плоскостью z*=0, жидкость находится в области 
, ось z* направлена против 
, ось x*- по направлению распространения волны.
Граничные условия на поверхности жидкости
,
, 
(2)
,
где u - нормальная скорость поверхности,
- нормаль к поверхности, внешняя к области, занятой жидкостью, К - средняя кривизна поверхности, 
- поверхностная плотность заряда, 
- давление в атмосфере, γ- коэффициент поверхностного натяжения.
Возмущения величин затухают на бесконечности по обе стороны от поверхности жидкости.
Уравнение поверхности жидкости запишем в виде 
. На поверхности: 
, в атмосфере 
, где 
- возмущение,
- невозмущенное поле. Аналогично: 
, 
.
Для установившихся бегущих волн предполагаем, что возмущения зависят от 
, где с - фазовая скорость. В качестве малого параметра примем 
, где 
- максимальная амплитуда поверхности, λ- длина волны, предполагаемая заданной величиной.
Введем безразмерные величины
, 
,
, 
, 
,(3)
, 
, 
.
Уравнения (1) принимают вид
, 
,
, 
.
Граничные условия (2) должны быть записаны в безразмерных обозначениях. Необходимо добавить также условия периодичности и симметрии волны относительно вертикали, проходящей через вершину волны, а также условие расположения оси x* на плоской поверхности жидкости.
В результате получим нелинейную краевую задачу для нахождения величин (3): 
, p, φ, Ē, σ, ξ, с. Для решения этой задачи применим метод малого параметра, использованный в [1] для исследования гидродинамических волн. Основная идея этого метода заключается в том, что многие дифференциальные уравнения, соответствующие конкретным физическим задачам, допускают введение безразмерного малого параметра δ, имеющего различный смысл в разных физических задачах, так что решение при 
может быть найдено легко. Тогда решение при 
ищется в виде ряда (не обязательно сходящегося) по степеням δ, такого, что нулевой член этого ряда соответствует решению краевой задачи при .
Затем находим выражения для 
, 
, 
, 
, 
, p*, 
, фазовой скорости с.
Форма поверхности определяется соотношением
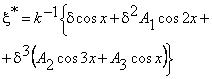(4)
где A1, A2, A3 - некоторые коэффициенты, зависящие от двух безразмерных параметров взаимодействия, характеризующих относительную величину капиллярных и электрических сил по сравнению с гравитационными:
, 
(5)
Выражение для горизонтальной составляющей скорости кроме периодических по времени слагаемых имеет еще постоянную составляющую
, 
,
где L - глубина частицы жидкости, c0 - фазовая скорость в линейном приближении (δ=0 ). Величина 
известна как переносная скорость Стокса.
Наибольшего значения скорость достигает на поверхности жидкости (L=0 ) . Если L→∞, то 
. Наличие поверхностного натяжения приводит к увеличению переносной скорости. Переносная скорость приводит к разомкнутости траекторий частиц жидкости, которые наряду с колебательным движением обладают также равномерным движением в направлении распространения волны. С учетом выражения линейной фазовой скорости запишем
,
, 
.
Отсюда следует, что при определенных значениях параметров 
и 
величина обращается в нуль. При 
поверхностная волна переходит в гравитационную [1].
Для каждого значения 
существует такая длина волны λ, для которой = 0. И наоборот, для каждого значения λ существует такое значение , при котором для этой волны = 0.
При Kc>>1 (короткие волны), выражение примет вид: 
. Вводя периоды колебаний волны 
и частицы 
, можно записать: 
Аналогично для частот: 
. Видно, что период колебаний частицы превышает период волны.
Выражение для высоты волны (расстояние по вертикали от уровня впадины при 
до уровня вершины при x=0) имеет вид
(6)
При выражение (6) совпадает с полученным в [1], при этом A2+A3= 0,5. В случае капиллярных волн (Kc >>1) можно пренебречь гравитационной и электрической силами, тогда
.
Следовательно, при увеличении поверхностного напряжения γ, амплитуда волны уменьшается. При 
величина A2+A3 ≈ -2,2.
Если 
, а 
, то
.
Выражение для фазовой скорости (при ) имеет смысл только при 
. При увеличении 
величина A2+A3 возрастает, начиная от A2+A3 = 0,5 при Ke=0. Следовательно, высота волны возрастает при увеличении напряженности 
, что хорошо согласуется с известными экспериментами [5]. При достаточно большом значении параметров 
величина A2+A3 становится отрицательной, что указывает на уменьшение высоты волны по сравнению со случаем Kc=Ke=0. Если Kc>Ke, то при амплитуда волны будет уменьшаться, при этом A2+A3 ≥ 6,5.
Выражения для амплитуды вершины
и впадины
находятся на основании (4). Очевидно, что 
. Разность между этими амплитудами равна
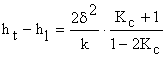(7)
Из (7) следует, что 
не зависит от электрического поля. При 
разность положительна, т.е. амплитуда вершины больше, чем впадины; при этом вершина уже (т.е. заострена), а впадина шире. При 
рассматриваемая теория неприменима. Если , то амплитуда у вершины меньше, чем у впадины.
Рассмотрим влияние электрического поля на фазовую скорость волны
(8)
где 
- параметр, зависящий от Kc и Ke. Из (8) следует, что с зависит от квадрата амплитуды волны. При 
выражение с принимает вид [1]: 
. При 
, 
выражение 
имеет вид
.
Отсюда при Kc=0 следует 
. Если 
, то 
.
Для Kc=0, Ke≠0 ( Ke<1) имеем:
.
Отсюда видно, что при увеличении Ke величина 
возрастает по модулю, оставаясь отрицательной. При Ke= 0 имеем = -0,5.
Из (8) следует, что при возрастании величина с при фиксированном k уменьшается и обращается в нуль при 
. При заданных γ и величина c0 достигает минимума при 
:
.
При 
величина 
обращается в нуль. Значению 
соответствует величина поверхностной плотности заряда
При 
поверхность становится неустойчивой - происходит ее разрушение. Различие между плотностью поверхностного заряда на вершине (x=0 ) и впадине ( ) равно
, 
,
где параметр В зависит только от Kc. Видно, что разность 
не зависит от электрического поля. Для Kc=0 имеем
т.е. плотность заряда на вершине больше, чем во впадине. Это приводит к тому, что электрическая сила на вершине волны больше, чем во впадине; т.е. электрические силы создают неустойчивость поверхности, стремясь вытянуть вверх острия на вершинах волн. Поскольку 
, разность 
будет положительной при всех реальных значениях параметров в выражении Kc.
СПИСОК ЛИТЕРАТУРЫ
- Алешков Ю.З. Теория волн на поверхности тяжелой жидкости. - Л.: Изд-во ЛГУ, 1981. - 196 с.
- Белоножко Д.Ф., Климов А.В., Григорьев А.И. // Сб. докладов VII Международной научной конференции «Современные проблемы электрофизики и электрогидродинамики жидкостей». - СПб: Из-во СпбГУ, 2003. - 316 с.
- Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. - М.: Наука, 1982. - 624 с.
- Ландау Л.Д., Лифшиц Е.М. Гидродинамика. - М.: Наука, 1986. - 736 с.
- Мелчер Дж. Р. // Магнитная гидродинамика. 1974. №2. С.3.
- Найфэ А.Х. Методы возмущений. - М.: Мир, 1976. - 456 с.