Все более актуальной в настоящее время становится проблема прогнозирования динамики развития региональных лесных комплексов. В качестве одного из этапов исследований по этой теме автором в содружестве с Гринпис России был выполнен описанный ниже проект. В рамках проекта была разработана соответствующая экономико-математическая модель. Последующая реализация модели на компьютере с использованием реальных данных показала ее эффективность для решения задач прогнозирования лесной отрасли.
Задачей данного исследования являлось создание методических основ построения макроэкономической математической имитационной модели для системы, состоящей из лесного хозяйства, лесной и деревоперерабатывающей промышленности и функционирующей в регионе со значительным антропогенным воздействием. В качестве региона для апробации модели был выбран Санкт-Петербург и область, где влияние человека на окружающую среду в последнее время существенно возросло.
С целью калибровки модели и проверки ее на соответствие реальности (верификации) начальным пунктом моделирования был выбран 1990 год, конечным - 2010. Изменение показателей модели времени представлено с помощью следующего уравнения:
Xt = Xt-1 + (X)´ Dt (1)
где
Xt - величина показателя в текущем периоде времени;
Xt-1 - величина показателя в предыдущем периоде времени;
(X)´ -производная X: (X)´ = dX/dt;
Δt - временной интервал.
Модель включает в себя следующие составные части (модули): лесные ресурсы региона; факторы окружающей среды; лесное хозяйство и лесная промышленность региона (потенциальное предложение древесного сырья, потенциальный спрос на древесное сырье, производство древесного сырья, цены на древесное сырье); деревоперерабатывающая промышленность региона (потенциальное предложение продуктов деревопереработки, потенциальный спрос на продукты деревопереработки, производство продуктов деревопереработки, рынки продуктов деревопереработки, производственные мощности деревопереработки); развитие народное хозяйства страны в целом (всеобщие факторы спроса).
Эти составные части были воплощены в модельных модулях, которые в данном тексте детально не описываются. Ниже приводятся лишь основные элементы, дающие представление о процедуре моделирования.
Модельный модуль, описывающий лесные ресурсы региона состоит из четырех блоков: лесопокрытая площадь, общий запас древесины, запас на гектаре, пользование (главное и промежуточное). Каждый блок разделен на две части: хвойные и лиственные породы.
При формировании блоков мы руководствовались следующими соображениями. Предполагается, что всю площадь под древостоем можно условно разделить на площади, относящиеся к определенной группе возраста. Такая дифференциация была произведена с шагом в 1 год. Естественно, что площадь древостоя, которому в 1990 году 1 год, относится в 1991 году уже к группе двухлетних насаждений и т.д. Площади, относящиеся к 1990 году, являются стартовыми показателями и вводятся в модель экзогенно. Площадь древостоя возраста 0 лет соответствует площади рубки и находится по формуле:
S0 = P / H ср.экспл., (2)
где
S0 - площадь древостоя возраста 0 лет (площадь рубки), тыс.га;
P - объем рубки, тыс. м3;
H ср.экспл. - средний запас на гектаре спелых и перестойных насаждений (после 70 лет для лиственных пород, после 100 лет для хвойных пород).
Запас по каждой группе возраста рассчитывается как произведение удельного запаса (на гектаре) насаждений соответствующей группы возраста и площади, находящейся под этими насаждениями.
![]() , (3)
, (3)
где
Vt - запас древостоя возраста t лет, тыс.м3;
Ht - удельный запас (на гектаре) древостоя возраста t лет, м3/га;
St - площадь древостоя возраста t лет, тыс.га.
Запас на гектаре рассчитывается в модели на основе уравнения роста численности биологических популяций (т.н. уравнение Ферхюльста-Пирла), модифицированное для описания хода роста древостоев ученым Санкт-Петербургской лесотехнической академии А.С. Алексеевым [1]:
![]() , (4)
, (4)
где
H- запас древесины, м3/га;
t - время (возраст), лет;
a- кинетический коэффициент, безразмерный;
K - максимально возможный запас древесины, м3/га.
В интегральной форме уравнение (4) имеет вид:
![]() , (5)
, (5)
где
E- коэффициент.
Применив метод прямоугольного интегрирования получаем:
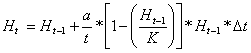 , (6)
, (6)
где
Ht - запас древостоя возраста t лет, м3/га;
Ht-1 - запас древостоя возраста (t-1) лет, м3/га.
С учетом влияния, которое оказывает рубка на удельный запас, уравнение (5) выглядит следующим образом:
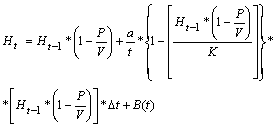 (7)
(7)
где
V - суммарный запас древесины, тыс.м3;
P - объем рубки, тыс. м3;
B(t) - интенсивность внешнего воздействия (суммарное влияние антропогенных факторов).
Эта формула используется в модели раздельно с учетом главного и промежуточного пользования. То есть для молодых и приспевающих древостоев в расчетах участвует объем рубок ухода (промежуточное пользование) и соответственно суммарные запасы древесины по этой возрастной категории. Для спелых и перестойных - объем главных рубок (главное пользование) и соответствующие суммарные запасы древесины.
Коэффициенты a, K, E уравнений (4) и (5) для Санкт-Петербургского региона (город и область) были получены с помощью процедуры Solver из пакета анализа MS Excel. Теоретические значения запаса древостоя (HТi) сравнивались с экспериментальными (HЭi), известными из таблиц хода роста. А критерий Пирсона, вычисляемый по формуле (8) являлся целевой функцией, которую следовало минимизировать, подбирая соответствующие значения коэффициентов.
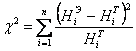 (8)
(8)
В результате с достаточной степенью достоверности были получены значения необходимых коэффициентов.
Оценка потенциального предложения древесного сырья была выполнена на основе предварительно рассчитанной кривой предложения, имеющей следующую форму:
Et=aE*Pi(t)pE1i *(Pi(t) /Pi(t-1))pE 2i , (9)
где
Et - предложение (заготовка) древесины в году ;
Pi(t) - цена сортимента i в текущем году t;
Pi(t) /Pi(t-1) - отношение цены текущего года к цене предыдущего года (t-1);
aE - константа;
pE 1i - долгосрочная эластичность предложения по цене сортимента i;
pE 2i - краткосрочная эластичность предложения по цене сортимента i.
Кривая предложения сформулирована в модели как зависимость "цена-количество". Кривая смещается вместе с изменением величины запаса древесины. Потенциальный объем выпуска отдельного сортимента вычисляется как произведение общего объема предложения древесного сырья на стандартные коэффициенты, отражающие возможный выпуск конкретного сортимента из 1 м3 сырья.
Аналогично рассчитывается потенциальный спрос на древесное сырье в целом и на отдельные сортименты. При этом общий потенциальный спрос на древесное сырье, производимое лесной промышленностью региона, определяется обязательно с учетом внешнего спроса, то есть спроса потребителей за пределами региона.
Фактически выпускаемое количество сортиментов каждого вида получается соответственно как минимум потенциального предложения и потенциального спроса.
Разница между объемом потребления древесины деревоперерабатывающей промышленностью и объемом предложения со стороны региональной промышленности образует региональный импорт сортиментов.
Потенциальное предложение продуктов деревопереработки отображается нелинейной кривой предложения. Для этого применяется функция предложения следующей формы:
AРЕГ j(t)=aA*Pj(t)pA j (10)
где
AРЕГ j(t) - региональное предложение продукта деревопереработки j в году t;
Pj(t) - цена продукта деревопереработки j в текущем году t;
aA - константа;
pA j - эластичность предложения по цене продукта деревопереработки j.
Потенциальная цена сортимента рассчитывается с помощью соотношения с ценой конкретного продукта деревопереработки, для производства которого используется данный сортимент.
Для первичного анализа лесного рынка Санкт-Петербурга и Ленинградской области были использованы данные областного Комитета по лесопромышленному комплексу, а также информация городского Комитета государственной статистики.
Цены продуктов деревопереработки определены как потенциальным спросом на эти продукты, так и потенциальным их предложением. Рынок образует равновесие между спросом и предложением, которому соответствует определенная цена. В расчетах как раз и была использована эта количественно-стоимостная взаимосвязь, которая, следует отметить, образуется не на региональном, а на глобальном уровне (то есть - уровне государства, группы регионов и т.п.).
Механизм определения цены продуктов деревопереработки возникает в результате исчисления соотношения "спрос/предложение". Для этого используются следующие формулы:
Pt =P(t-1) + FP*Δt , (11)
FP = [(NЕЧ (t-1)/AЕЧ (t-1)) - 1)]*P(t-1) , (12)
где
P - цена продукта деревопереработки;
FP - темп изменения переменной цены;
NЕЧ - потенциальный спрос в европейской части России на продукт деревопереработки;
AЕЧ- потенциальное предложение европейской части России продукта деревопереработки;
Δt - временной интервал, с которым производится имитация.
Индекс "t" означает текущий период, "t-1" - предыдущий.
Европейская часть России принята как глобальный уровень, определяющий цены на продукцию деревопереработки, в частности, для Санкт-Петербургского региона.
Для определения цен на продукты деревопереработки необходимо определить эконометрическую взаимосвязь между объемами производства деревоперерабатывающей промышленности региона и потенциальным предложением продуктов деревопереработки внутри европейской части России в целом. Европейская часть России в данном случае фигурирует как надрегиональная структура, т.к. продукция лесной индустрии, произведенная в каждом из ее регионов может свободно перемещаться внутри нее. Предложение продуктов деревопереработки внутри европейской части России (AЕЧ) условно можно разделить на предложение исследуемого региона (AРЕГ) и предложение всех остальных регионов (AОР):
AЕЧ = AРЕГ + AОР (13)
Функция спроса NЕЧ должна быть оценена эконометрически и иметь следующую форму:
NЕЧ = aN * (BIPK)bN * (Pj)pN (14)
где
NЕЧ - потребление на душу населения;
BIPK - доходы на душу населения (удельная величина валового внутреннего продукта);
Pj - цена продукта;
aN - константа;
bN - эластичность спроса по доходам;
pN - эластичность спроса по цене.
Общий потенциальный спрос на продукты деревопереработки образуется из потенциального внутреннего спроса и внешнего спроса, так называемого нетто-экспорта.
Региональное производство определено в модели как минимум среди двух величин: предложения в соответствии с кривой предложения и производственной мощности соответствующего сектора деревоперерабатывающей промышленности.
Факторы общеэкономического развития учтены в модели с помощью переменных, отражающих рост народонаселения и рост валового внутреннего продукта на душу населения. Для этого были использованы следующие формулы:
BEVt = BEV(t-1) + FBEV*Dt , (15)
FBEV = TEMPOFBEV *BEV(t-1) (16)
BIPKt = BIPK(t-1) + FBIPK*Dt (17)
FBIPK=TEMPOFBIPK *BIPK(t-1) (18)
где
BEV - численность населения;
FBEV - темп изменения переменной, отражающей численность населения;
TEMPOFBEV - среднегодовой рост численности населения;
BIPK - доход на душу населения;
FBIPK - темп изменения переменной, отражающей доход на душу населения;
TEMPOFBIPK - среднегодовой рост дохода на душу населения.
Производственная мощность региональной деревоперерабатывающей промышленности определяется уровнем маржинального дохода. Соотношение величины маржинального дохода с соответствующим контрольным значением обусловливает изменение мощности.
Одной из основных составляющих при оценке перспектив изменения объемов производства продукции деревопереработки является динамика производственной мощности. Для того, чтобы отразить механизм изменения производственной мощности была выбрана следующая процедура. Искомые изменения были поставлены в соответствие к маржинальному доход, образующемуся в подотраслях деревоперерабатывающего сектора. Он представляет из себя прибыль в сумме с постоянными затратами предприятия.
Изменения производственной мощности в модели обусловливали соотношения фактической и нормативной величин удельного веса маржинального дохода в выручке от реализации:
Проведенная на основе статистических тестов верификация модели показала ее соответствие реальности.
Цель моделирования - имитация развития системы лесного хозяйства, лесной и деревоперерабатывающей промышленности региона при определенных изменениях экзогенных факторов. Эти гипотетические изменения учитываются в имитационных сценариях. Их отличия от базисной имитации или, иными словами, имитации со стандартными значениями всех показателей, и являются реакцией системы на внешние воздействия.
С целью апробации модели были сформированы два сценария с различными значениями показателей внешнего воздействия на региональную систему лесного комплекса. В качестве определяющих внешних антропогенных факторов были выбраны мероприятия по уходу за лесом и загрязнение воздуха.
В итоге интенсивность внешнего воздействия для первого "позитивного" сценария была принята такой, что за период с 2002 г. по 2010 г. запас на гектаре увеличивался бы на 10%, а для второго "негативного" сценария - уменьшался бы на 10%.
В результате, после имитации были получены основные параметры регионального лесного комплекса, соответствующие двум сценариям:
Изменения древостоя заключаются в том, что по сравнению с 2000 г. в 2010 г. общий запас древостоя хвойных пород увеличится при базисной имитации на 3,5%, при реализации 1-го сценария - на 4,1%, при реализации 2-го сценария - на 2,9%. Запас древостоя хвойных пород сократится при базисной имитации на 12,3%, при реализации 1-го сценария - на 11,3%, при реализации 2-го сценария - на 13,2%
Анализ результатов моделирования показал, что в результате реализации имитационных сценариев, изменения коснутся только объемов производства древесного сырья. Согласно базисной имитации производство древесины в 2010 г. буде находиться на уровне 2000 г., согласно 1-му сценарию увеличится на 0,7%, согласно 2-му сценарию уменьшится на 0,7%. Средняя цена на древесину вне зависимости от сценариев должна увеличиться к 2010 г. на 3,7%; объемы производства продукции деревопереработки - на 8,1%, цена на продукцию деревопереработки - на 3,7%.
В качестве выводов по данной работе необходимо отметить следующее. Лишь в некоторых исследовательских работах в области макроэкономики изучены в совокупности факторы влияния на предложение, спрос и цену древесины и продуктов ее переработки, сделаны выводы о причинах развития лесного рынка. Очевидно, что нужно исследовать не отдельные составляющие рынка, например, спрос вне зависимости от предложения, а пытаться отобразить всю систему лесного хозяйства, лесной и деревоперерабатывающей промышленности в совокупности. Кроме того, существенно также и то, чтобы система координат внутри которой действует система лесного комплекса была правильно сориентирована: необходимо изучение не только настоящей, но и будущей динамики экономического и экологического окружения системы. Экологическая ситуация вокруг лесных (лесопромышленных) предприятий определяет состояние лесов, и должна быть оценена с точки зрения долгосрочной гарантии их функционирования. Частота экстремальных воздействий на лесную экосистему должна быть соотнесена с "нормальными" местными условиями, в которых экосистема должна функционировать. Размер пользования лесной системой, который соответствует определенным производственным требованиям, зависит от вида и интенсивности хозяйственной эксплуатации. В целом, экологическая ситуация, в которой находится лесной комплекс, зависит как от внутренних, так и от внешних факторов. Принимая во внимание эти и другие соображения, была создана рассмотренная выше модель. С ее помощью стало возможным изучение долгосрочной динамики различных экономических аспектов производства древесины и продуктов ее переработки при изменении условий окружающей среды.



