Экологами наблюдалось значительное количество систем «хищник - жертва» с явно противоречивым поведением. Так, существуют случаи, когда хищничество оказывает сильное разрушающее воздействие . Вместе с тем существуют данные, что во многих случаях популяция хищников (рыси) не оказывает заметного влияния на динамику численности своих жертв(занцев). В ряде случаев численность популяции хищников следует за численностью жертв. В частности, хорошо известен факт более столетних колебаний численности американского зайца (беляка) и канадской рыси, благодаря данным компании «Гудзонов залив».
Попытки описания этих колебаний в рамках традиционной модели Лотки -Вольтерра оказались неудачными [1]. Символично название статьи [2]: «Едят ли зайцы рысей?». Долгое время это название воспринималось как шутливое или ироничное. Последнее связано с тем, что параметризация указанных моделей по результатам колебаний зайцев и рысей оказывалась более успешной, если в модели зайцы заменялись рысью, а рыси - зайцами. В настоящее время вопрос, поставленный в заголовке этой статьи, по нашему мнению, требует более серьезного рассмотрения.
Известно, что первые математические .модели для системы «хищник - жертва» были представлены моделью «Лотки - Вольтерра» в двадцатых годах прошлого века и обладали свойствами нейтральности колебаний. Эти модели не удовлетворяли критерию «грубости) динамических систем. Что, впрочем, могло быть обнаружено лишь по прошествии определенного времени, т.к. само понятие грубости динамических систем было введено А.А. Андроновым и Л.С. Понтрягнным только в 19.17 г.
Развитие математических моделей систем «хищник - жертва» идет сейчас по пути все большего учета реальных свойств системы, которые сохраняют относительную общность и относительную простоту. Такие модели, по сравнению с моделью «Лотки -Вольтерра» включают в себя внутривидовую (в популяции жертвы) конкуренцию, различные трофические функции хищника нелинейный характер скорости размножения жертвы (эффект Олли) и т.д.
Широкое использование вычислительной техники и численных методов в моделировании экологических систем позволило сравнительно просто исследовать системы трех трофических уровней, например: «продуцент - консумент - хищник» по терминологии [3]. Кроме того, вычислительные машины позволили сравнительно просто учесть воздействие случайных факторов на экологическую систему Возвращаясь к системе «заяц - рысь» следует заметить, что в фундаментальной монографии [4]
«.....Хищники, скорее всего, следуют за колебаниями численности зайца, а не вызывают их. Все же колебания, вероятно, выражены более отчетливо благодаря высокому отношению числа хищников к числу жертв в период снижения численности зайца, а также благодаря их низкому отношению в период, следующий за минимумом численности зайцев, когда они, опережая хищника, восстанавливают свою численность. Кроме того, при высоком отношении численности рыси к численности зайца хищник поедает большое количество боровой дичи, а при низком отношении - небольшое, Это, по-видимому, служит причиной возникновения колебаний численности у этих второстепенных растительноядных животных. Таким образом, взаимодействие зайцы -растения вызывает колебания численности зайца, хищники повторяют колебания их численности, а циклы численности у растительноядных птиц вызваны изменением пресса хищников. Очевидно, что простые модели полезны для понимания механизмов колебания численности в природных условиях, но эти модели объясняют возникновение этих колебаний далеко не полностью...».
В рассматриваемом случае, на территории от Аляски до Ньюфаундленда определяющими взаимоотношениями являются взаимоотношения заяц - продуцент. Заяц - беляк преобладает среди растительноядных животных региона; он питается кончиками побегов многочисленных кустарников и небольших деревьев. Сильное объедание растений приводит к тому, что растения образовывают побеги с высоким содержанием ядовитых веществ, что делает их несъедобными для зайцев.
Растения остаются защищенными таким образом в течение 2 - 3 лет после сильного объедания. Это приводит к задержке между началом снижения численности зайца и восстановлением его кормовых запасов. Хищники же следуют за колебаниями численности зайцев, а не вызывают их. Если руководствоваться этой гипотезой, то математическая модель не должна ограничиваться взаимодействием заяц - рысь, а должна содержать три трофических уровня. Кроме того, модель взаимодействия «заяц -продуцент» должна обеспечивать предельный цикл при некоторых значениях параметров.
Вторым принципиально важным моментом является учет конкуренции хищников (рыси) за жертву, которая до настоящего времени практически не использовалась при моделировании экосистем.
Для сравнения результатов расчетов с экспериментальными данными математическая модель должна описывать воздействие случайных факторов внешней среды на динамику трехуровневой системы.
В основу трехуровневой системы нами была положена модель Розенцвейга и Мак -Артура, описывающая взаимодействие заяц - продуцент и обладающая предельным циклом.
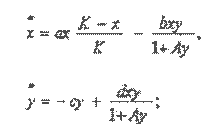
В размерном виде эта модель имеет вид:
 (1)
(1)
где х, у - плотности численности продуцента и популяции зайцев (консумента); К - емкость среды продуцента, а - мальтузианский параметр, b - коэффициент удельной скорости потребления популяции продуцента зайцем: с - коэффициент естественной смертности в популяции зайцев; d - коэффициент скорости потребления консументом биомассы продуцента; А - постоянный коэффициент,
В этом случае описание колебаний в системе зайцы - рыси сводится к построению такой модели для рыси, которая не разрушала бы автоколебаний в системе (1), т.е. предельные циклы в системе продуцент - зайцы должен быть инвариантным относительно интродукции в системе хищника (рыси).
Естественно предположить, что пренебрежимо слабая конкуренция хищников за жертву (зайцев) реализуется при стремлении к нулю плотности популяции хищника, а предельно острая конкуренция - при неограниченно растущей его популяции Для промежуточных плотностей популяции хищников трофическая функция принимает следующий вид;
![]() (2)
(2)
где: 1/ р - плотность популяции хищника, при которой его рацион вдвое меньше, чем в отсутствии конкуренции за жертву. Возможны, разумеется, и другие способы описания конкуренции хищников за жертву, однако, предлагаемый прост, естественен и не противоречит экспериментальным данным,
В этом случае система уравнений (1) принимает вид:
 (3)
(3)
где z - плотность популяции хишннка, f- коэффициент естественной смертности; g - коэффициент скорости потребления хищником биомассы консумента, е -коэффициент удельной скорости потребления хищником биомассы консумента, В -постоянный коэффициент
Введем следующее обезразмеривание системы уравнений (3):
![]() (4)
(4)
Подобное обезразмеривание позволяет значительно уменьшить число параметров системы (3) и записать ее в виде:
 (5)
(5)
В этих уравнениях параметры ε1, ε2, α1, α2, γ1, γ2 связаны с параметрами системы (3) следующими зависимостями;
![]() (6)
(6)
Такое обезразмеривание приводят к возможности более точного описания природных; закономерностей в силу агрегирования параметров системы (3). Система уравнений (5) описывает следование численности хищника (рыси) за численностью жертвы (зайца), а следовательно и «пресс» жертвы на хищника (по аналогии с прессом хищника).
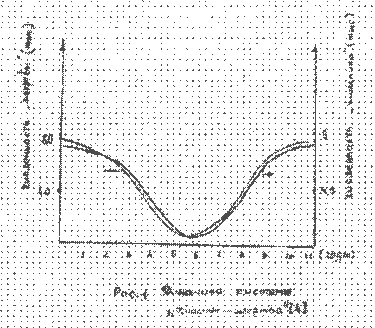
Рисунок 1.
Исследование влияния возмущений на динамическую систему хищник - жертва -продуцент проводилось на основе уравнений Ланжевена[5-6]:
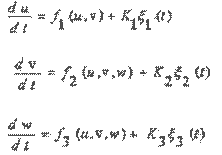 (7)
(7)
где; K1 ~ 0,002; К2 « 0.0072; К3 = 0.001; ξ1(t), ξ2(t), ξ3(t) - независимые нормализованные гауссовские белые шумы.
Решение системы (7) проводилось численно с использованием неявной схемы Эйлера [6]. Параметры модели находились из сравнения с экспериментальными данными по условиям существования предельного цикла.
Результаты расчета представлены на рис.2 - рис.4. Экспериментальные значения колебаний численности рысей и зайцев как более достоверные брались sa последние пятьдесят лет статистики компании «Гудзонов залив», т.е. за 1890 - 1940 годы.
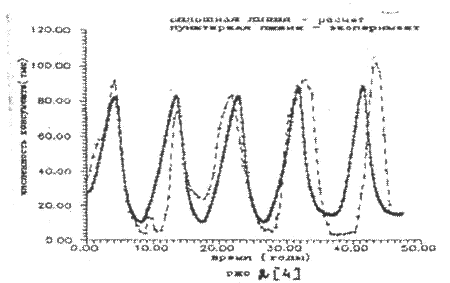
Рисунок 2.
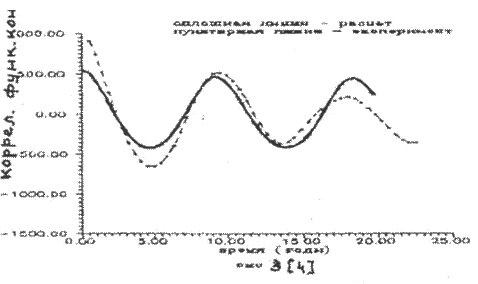
Рисунок 3.
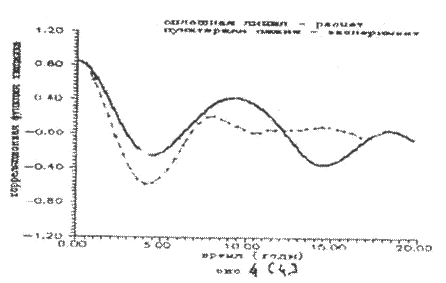
Рисунок 4.
Как следует из рисунков математическая модель трехуровневое системы (7) удовлетворительно описывает экспериментальные данные по колебаниям численности зайцев и рысей. Небольшое расхождение автокорреляционной функции дая хищника (рис. 4) может быть объяснено недостаточной точностью доступных экспериментальных данных по колебаниям рыси.
Хотя авторы классических экологических моделей и давали своим работам красивые многообещающие заголовки типа «математическая теория борьбы за существование», всем было совершенно ясно, что, сколько - нибудь поддающиеся исследованию классическими методами математические модели в виде дифференциальных уравнений слишком просты, чтобы, в самом деле описывать реально существующие природные сообщества Наоборот, признание того факта, что и специально созданные лабораторные сообщества тоже плохо согласуются с видениями пророков, потребовано длительной экспериментальной работы. Давным-давно, примерно во времена Дарвина, сложилась, бесспорно, правильная в общих чертах картина функционирования экологических сообществ. Согласно этой картине, любая природная экологическая система состоит из трех крупных групп видов, называемых трофическими уровнями, а именно из:
1. продуцентов (обычно это фотосинтезирующие зеленые растения), которые используя солнечную энергию, синтезируют органическое вещество из углекислого газа воздуха и простейших неорганических соединений;
2. консументов, которые питаются этой органикой, а «мирными» консументами, в свою очередь питаются хищники: будучи раз созданной, органика проходит дальнейшие звенья круговорота вещества;
3. редуцентов, которые разлагают метаболиты и органическое вещество погибших продуцентов и консументов на такие простые соединения, которые могут быть вновь использованы продуцентами.
Простейшие оценки показывают, что длительное существование экосистемы возможно только за счет круговорота вещества Если бы этот круговорот, в каком - то звене остановился, то имеющиеся в доступном для экосистемы виде запасы вещества, из которого строятся живые организмы, скоро бы оказались исчерпанными. Говорят также о круговороте вещества и энергии, имея в виду, что в органическом веществе запасена определенная химическая энергия, которая, в конечном счете, берется из энергии солнечного излучения.
При более детальном изучении конкретной экосистемы каждый трофический уровень разбивается на более мелкие, а если основной единицей экологии считать биологический вид, то общее число таких единиц в любой реальной экосистеме колоссально, а трофические (и иные) взаимосвязи между ними невообразимо сложны. Нельзя думать, чтобы подобные взаимосвязи можно было описать моделью в виде, скажем, системы дифференциальных уравнений, которая подавалась бы исследованию в классическом смысле, т.е. интегрированию в формальном виде или хотя бы качественному исследованию
Ряд печальных опытов убедил человечество в том, что экосистемы нужно изучать в целом, не ограничиваясь лишь теми видами, которые для человека представляют экономический интерес. В этой связи можно говорить, например, о концентрации в отдельных звеньях трофических цепочек некоторых ядов, которые попадают в природную среду с промышленными отходами, казалось бы, в сильно разбавленном и потому безопасном виде. Они, однако, могут быть накоплены живыми организмами и, в конце концов, попасть обратно в пищу человека в концентрированном виде. Можно привести и сколько угодно примеров гибели экосистем из - за повреждения каких - то звеньев круговорота вещества и т.д. Итак, экосистемы хорошо было бы исследовать в целом, и притом на количественном уровне, тем более что грубые количественные оценки типа общей продукции органического вещества и его потребления на разных трофических уровнях делаются уже достаточно давно.
Конечно, вновь обсуждаются старая физико- математичекая идея - сначала описать протекание процессов в малом с помощью дифференциальных уравнений, а затем средствами математики решать эту систему. Но за невозможностью формульного исследования достаточно сложных систем, эта всегда существующая подспудно идея извлекалась на свет Божий до середины XX века, когда началась революция в области вычислительных методов и вообще обработки информации, связанная с применением ЭВМ, Не забудем, что это была эпоха разгара холодной войны, так что все первые и многие последующие ЭВМ строились, в первую очередь, для военных целей.
Когда вооруженные силы противостоящих блоков были достаточно насыщены боевой техникой всякого рода, в том числе и вычислительными машинами, - достаточно в том смысле, что взаимное полное уничтожение сделалось вполне реальным. Вычислительные машины широким потоком хлынули и в мирные приложения. В отличие от военных вычислительных организаций, они сделались относительно общедоступными. Примерно в начале 60 - х годов каждый настойчивый ученый и, в частности, эколог мог пробиться к ЭВМ для проведения интересующих его расчетов. Вычислительные трудности во многих случаях отступили на второй план, и стало уместно вспомнить о другом принципиальном затруднении, чтобы систему дифференциальных уравнений вообще стоило решать, надо, чтобы динамику изменения системы в малом она описывала чрезвычайно точно.
Какова же вообще может быть точность измерения биологических параметров, характеризующих скорости протекания тех или иных процессов? (Обратимся к таким областям биологии, в которых измерения ведутся достаточно давно, например, к физиологии дыхания или фотосинтеза. Итак, с какой точностью может быть известно потребление кислорода особью, итак это тот же вопрос относительно скорости фотосинтеза. В ответ на подобные вопросы биолог называет обычно цифру порядка 20 %.
Почему же биолог называет столь матую точность? Неужели за 100 с лишним лет, в течение которых ведутся измерения в области физиологии, наука не научилась точнее определять потребление кислорода? Ответ обескураживает, дело, конечно, не в точности химического анализа, а в том, что разные особи одного вида при фиксированных внешних условиях действительно имеют несколько различное потребление кислорода - отсюда и берутся эти 20%. В биологии нет фундаментальных констант типа заряда электрона или скорости света в вакууме, которые - вне всякого сомнения - постоянны. Или, если угодно, особи одного и того же вида несколько различаются между собой, в отличие от электронов или квантов света.
Теперь понятно, что трудность точного задания системы уравнений, описывающая динамику экосистемы, действительно является фундаментальной. Издавна экологи изображают экосистемы графически, рисуя на листе бумаги кружками их различные составляющие части, а стрелочками между кружками изображая взаимодействия. Получается такая восхитительная путаница кружков и стрелочек, что и разобраться в ней невозможно, не говоря уже о том, чтобы все эти взаимодействия оценить количественно.
Вывод заключается в том. что математическое моделирование любой экологической системы (кроме, может быть, некоторых систем биотехнологии) представляет собой обширный, продолжительный и дорогостоящий эксперимент, который имеет очень мало шансов наудачу. Нужно, однако, объяснить, что понимать под «удачей» или «неудачей» отдельного такого эксперимента и всего направления эколого -математического моделирования в целом (оно еще называется «системным анализом экологических сообществ). Здесь возможны два подхода, так сказать «жесткий» и «мягкий». Мягкий подход, что несмотря на формальный экспериментальный провал рассматриваемых моделей, экологическое научное сообщество все - таки научилось с их помощью некоторым вещам очень важным, даже с практической точки зрения. Мягкий подход к оценке достижений моделирования сложных систем мог бы состоять в том, что в процессе работы в этой области образования некий новый научный эгрегор, состоящий из математиков и биологов, нашедших общий язык и возможность совместной научной работы, Часть математиков, физиков и программистов получила возможность уйти в биологию из физики, техники и военных применений, и это есть некое крупное всемирное движение, которое уже принесло и еще принесет немало полезного [7-9].
Колебания численности зайцев и продуцента достаточно хорошо описаны в [наблюдающиеся на северных островах Канады, имеют большое значение для теории сложных иерархических систем. Полученные диссипагивные структуры, представляют большой интерес, для интенсивно развивающейся в настоящее время математической экологии. Основной результат, проведенного анализа, заключается в том, что показано, как из весьма простых и естественных положений о характере межвидовых взаимоотношений возникает достаточно сложное поведение системы хищник - жертва -продуцент Математическая модель описывает широкий спектр процессов и явлений, которые характерны дня сложных экологических систем. Работа выполнена при финансовой поддержке РФФИ (03 - 03 - 96332).
Литература.
- В.Н. Тутубалин, Ю.М. Барабашева, Л.А. Григорян, Е.Г. Унтер. Математическое моделирование в экологии. Ист ори ко - методологический анализ / Из - во «Языки русской культуры», М.. 1999, С. 356.
- М.Е. Gilpia Do hares eat lynx.? //Amer. Nature., 1973, v. 107, № 957, p. 727 - 730.
- А.Д. Базыкнн. Математическая биофизика взаимодействующих популяций, /М.: из - во «Наука», 1985, С, 185,
- Бигон, Дж. Харпер, К. Таусенд. Экология. Особи, популяции и сообщества. / М.: из - во «Мир», 1989, т. 1,2.
- B.C. Аншценко. Сложные колебания в простых системах. / М.: из - во «Наука», 1990, С. 380.
- ДФ. Кузнецов. Численное моделирование стохастических дифференциальных уравнений и стохастических интегралов, / Санкт -Петербург, «Наука», 1999.С 458.
- Д. М. Андеосек. Экология и наука об окружающей среде. / Л.: из-во «Гидрометеоцентр», 1985, С. 161.
- А.Я. Федоров. Предельные циклы в системе «хищник - жертва» / Сб. статей «Актуальные проблемы медицины и биологии», вып. 2, 2003, С. 99-102.
- Н.Н. Моисеев. Расставание с простотой. / М.: из - во «АГРАФ», 1989, С. 472.



