Пример 1. Одним из главных объясняющих факторов в пилении древесины является скорость инструмента, которая изменяется до 120 м/с в различных деревообрабатывающих станках. На основе физической сущности работы дисковой пилы с различными формами зубьев при стружечном и бесстружечном способах продольного пиления древесины была структурно определена регрессионная модель вида [2]
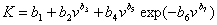 , (1)
, (1)
где К - удельная работа резания, Дж/м3.
Модель (1) содержит три слагаемых, то есть составляющих статистической модели. Значение b 1= k 0 характеризует заданные условия работы дисковой пилы, а также влияние неучтенных факторов, например, потери на неточности изготовления и погрешности заточки зубьев, погрешности установки пилы на пильный вал и т.п.
Вторая слагаемая модели (1) учитывает увеличение сил инерции от действия стружки и опилок. С повышением v > 60 м/с происходит повторное измельчение опилок, попадание мелких частиц в зазор между боковыми поверхностями полотна пилы и заготовки древесины. В итоге возрастают вредные силы трения, растет амплитуда колебаний пилы о бокам. Это еще более увеличивает сопротивление движению зубьев в древесине. При чрезмерном увеличении v при постоянной скорости подачи заготовки на пилу начинается процесс скобления зубьев о дно пропила, удельная работа при этом резко возрастает.
Третья слагаемая характеризует биотехнический закон. При этом степенная зависимость учитывает увеличение динамической прочности древесины от ударного воздействия зубьев о древесину, особенно при входе в заготовку. Таким образом, третья составляющая - это характеристика действия заготовки на инструмент (смысл K : это среднее сопротивление прониканию пилы в образец или заготовку древесины).
Степенная зависимость b 6 v b 7 учитывает снижение прочности древесины в зависимости от других факторов, возникающих в процессе резания. С увеличением скорости инструмента в квадратичной зависимости возрастает температура нагрева древесины в зоне контакта зуба с клетками древесины и она может достичь до 700-900 0С и более на вершине зуба и до 200-230 0С по дну пропила. С ростом температуры прочность древесины уменьшается по экспоненциальной зависимости, поэтому удельная работа резания (как показатель средней напряженности в зоне резания) также уменьшается. Древесина является упруго - вязко - пластическим материалом, поэтому с увеличением v меняются её физико-механические свойства.
На снижение значений K оказывает влияние также изменение коэффициента трения, который по данным многих исследователей возрастает при изменении v до 20-30 м/с, а затем уменьшается.
Удельная работа резания древесины является комплексным (системно производным) показателем, косвенно отражающим характер протекания физико-химических и механических явлений в зоне резания. Третье слагаемое модели (1) хорошо описывает изменение K при v = 5...50 м/с, а второе - при v > 40-50 м/с.
По экспериментальным данным проф. Н.К. Якунина была получена трехфакторная математическая модель [2] удельной работы резания
(x 107 Дж/м3)
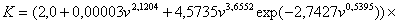
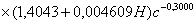 , (2)
, (2)
где: c - подача на зуб, мм; H - высота пропила, мм. Сумма квадратов отклонений 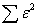 = 3,0055; среднеквадратичное отклонение
= 3,0055; среднеквадратичное отклонение 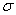 = 0,2381 107Дж/м3; коэффициент изменчивости V^ = 4,72%; показатель точности P^ = 0,64%; максимальная относительная погрешность
= 0,2381 107Дж/м3; коэффициент изменчивости V^ = 4,72%; показатель точности P^ = 0,64%; максимальная относительная погрешность 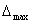 = 13,7%. Доверительная вероятность формулы (2) будет не ниже 86,3%.
= 13,7%. Доверительная вероятность формулы (2) будет не ниже 86,3%.
Пример 2. В некоторых ситуациях статистического моделирования приходится выполнять структурную идентификацию по имеющимся исходным данным. Чаще всего такой случай возникает тогда, когда однофакторная зависимость уже по смыслу ясна, причем из-за взаимного расположения измеренных точек x^, y^ , однако при этом не ясен выбор того или иного фрагмента биотехнического закона. Например, приходится выбирать из двух вариантов фрагментов - закона показательного или закона экспоненциального роста.
По данным [3] возраст A 0 до высоты ствола дерева на уровне груди человека при H = 1,3 м (для ели) в зависимости от бонитета изменяется по следующим данным
|
Бонитет |
2 |
3 |
4 |
5 |
|
A 0, лет |
15 |
35 |
40-45 |
55-60 |
Здесь возможны два методических подхода: во-первых, принять средне интервальные значения по размытым множествам, например:
Б = 4, A 0= 42,5 лет; Б = 5, А 0 = 57,5 лет; во-вторых, выполнить идентификацию модели по двум границам интервалов. В связи с тем, что изменчивость таксационных измерений высока, то, в зависимости от целей исследования, принимается первый или второй подход. Поэтому на практике нужны все три модели интервально заданных параметров.
Необходимо также отметить, что любая модель хорошо идентифицируется по тем исходным данным, если присутствуют значения при условии x = 0 , то есть на границе объясняющей переменной. В данном случае Б = 0 не имеет в литературе объяснения (что означает нулевой класс бонитета для характеристики условий местопроизрастания деревьев?), а вот по значению объясняющей переменной Б = 1 отсутствуют реальные данные А 0 . Аналогичные случаи практически возникают часто (из-за загромождения разными условностями для упрощения не автоматизированных расчетов) и их можно разрешать только подбором кодовой шкалы. В данном примере мы не знаем, как представляют лесоводы понятие «идеальный бонитет» (это как в биологии чашка Петри?) и какую кодовую шкалу они предложили бы, исходя из понятия «идеальное местопроизрастание». В будущем эту эвристическую задачу необходимо разрешить.
Из простого сопоставления пар исходных данных x^, y^ замечаем, что модели A 0 = Б и А 0 = А 1 Б не подходят и они слишком «грубы». Вот здесь мы и подходим к пониманию «нульмерной модели» по Н.Н. Моисееву [4]. Отбрасывая последовательно «очень грубые» модели, исследователь должен остановиться на какой-то последовательности усложнения конструкции статистической модели.
Та структура, которая будет удовлетворять содержательно и количественно (по адекватности) и станет «нульмерной» моделью. При этом, конечно же, необходимо соблюдать три основных условия (состояния) задачи, решаемой с помощью экспертной системы (один исследователь с ПЭВМ при идентификации также является экспертной системой, а другие эксперты подключаются как бы косвенно с помощью их научных публикаций), которые изложены в книге [5. с.83]:
- пространство поиска должно быть большим;
- знания предметной области должны быть достоверными (в нашем примере мы верим, что в работе [3] доказана возможность существования А 0 = f (Б) для деревьев);
- представляемые пользователем исходные данные должны быть достоверны (поверим автору [3] и по количественным данным).
Примем уравнение аллометрического роста 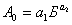 для идентификации вышеприведенных данных (напомним, что здесь возможна и линеаризация для аппроксимации, однако из-за скедастических свойств исходных лесотаксационных данных лучше даже в простых случаях применять идентификацию, что дает более точные статистические модели).
для идентификации вышеприведенных данных (напомним, что здесь возможна и линеаризация для аппроксимации, однако из-за скедастических свойств исходных лесотаксационных данных лучше даже в простых случаях применять идентификацию, что дает более точные статистические модели).
Вышеуказанная модель является «нульмерной» из следующих соображений, относящихся и к росту деревьев, а именно [6, с.7]: «Развитие подчиняется экспоненциальной или степенной зависимости и что имеется четкая регулярность в смене эволюционных этапов революционными перестройками. Чем значительнее революционные перестройки, тем реже они происходят и тем в более высокой степени фигурирует это число (то есть основание натуральных логарифмов)».
Формирование деревом годовых слоев действительно происходит сменой революционных и эволюционных перестроек, возбуждаемых сезонным изменением биоклиматического потенциала места произрастания.
Исходя из рассуждений запишем последовательность идентифицированных моделей ( Б =2...5), приведенных в табл. 1:
М1: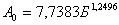 ; (3)
; (3)
М2: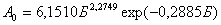 ; (4)
; (4)
М3: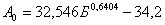 ; (5)
; (5)
М4: 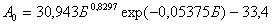 . (6)
. (6)
Сумма остатков по табл. 1 от модели к модели уменьшается. Добротность регрессионной модели, как это известно, намного лучше, если выполняется условие 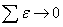 . В этом случае линия регрессии как бы находится в средневзвешенном положении относительно фактических значений показателя. Поэтому критерию добротности
. В этом случае линия регрессии как бы находится в средневзвешенном положении относительно фактических значений показателя. Поэтому критерию добротности ![]() лучше всех М4. Эта модель по остаткам имеет циклическую закономерность типа добавки, то A´ 0 есть
лучше всех М4. Эта модель по остаткам имеет циклическую закономерность типа добавки, то A´ 0 есть
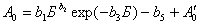 , (7)
, (7)
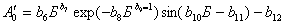 . (8)
. (8)
Далее можно было бы по остаткам модели М4 идентифицировать еще дополнительно модель (85). Однако по имеющимся ориентировочным данным такое уточнение не имеет большого содержательного смысла. Поэтому можно выдвинуть рабочую гипотезу «на будущее», что дробление кодовой шкалы бонитета леса дало бы возможность получения более эвристически богатой матрицы данных.
Таблица 1. Влияние бонитета леса на возраст дерева ели до высоты на уровне груди
|
Бонитет |
A^ 0,лет |
A 0,лет |
|
|
|
Класс надежности расчетов |
|
2 3 4 5
2 3 4 5
2 3 4 5
2 3 4 5 |
15.0 35.0 42.5 57.5
15.0 35.0 42.5 57.5
15.0 35.0 42.5 57.5
15.0 35.0 42.5 57.5 |
18.40 30.54 43.75 57.82
16.72 31.51 45.44 56.57
16.54 31.58 44.89 57.03
15.98 32.11 45.43 56.49 |
-3.40 4.46 -1.25 -0.32
-1.72 3.49 -2.94 0.93
-1.54 3.42 -2.39 0.47
-0.98 2.89 -2.93 1.01 |
Модель М1
-0.51 Модель М2
-0.24 Модель М3
-0.03 Модель М4
-0.01 |
-22.67 12.74 -2.94 -0.56
-11.47 9.97 -6.92 1.61
-10.27 9.77 -5.62 0.82
-6.53 8.26 -6.89 1.76 |
D
C
C
|
Примечание: Максимальные значения 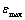 и
и 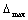 выделены.
выделены.
Из сравнения у моделей табл. 1 относительных погрешностей видно, что:
- максимальные значения
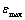 и
и 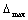 не совпадают по наблюдениям, поэтому значение
не совпадают по наблюдениям, поэтому значение 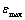 не может быть принято в качестве критерия адекватности, как это принято в математической среде «Эврика»; лучше по информативности среда CurveExpert-1.3;
не может быть принято в качестве критерия адекватности, как это принято в математической среде «Эврика»; лучше по информативности среда CurveExpert-1.3; - значение
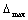 =8,26% наблюдается для модели М4, поэтому она принимается по максимальной относительной погрешности за лучшую версию модели.
=8,26% наблюдается для модели М4, поэтому она принимается по максимальной относительной погрешности за лучшую версию модели.
Доверительная вероятность будет равна, если учитывать по предельным значениям погрешности (максимального риска), значению 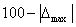 . Тогда можем установить классы надежности расчетов (последний столбец табл. 1). Модель М4 имеет более близкую к классу B надежности расчетов. Если бы мы считали по формулам (3 - 8) из классической статистики, то так и случилось бы, что доверительная вероятность достигается не менее 95%.
. Тогда можем установить классы надежности расчетов (последний столбец табл. 1). Модель М4 имеет более близкую к классу B надежности расчетов. Если бы мы считали по формулам (3 - 8) из классической статистики, то так и случилось бы, что доверительная вероятность достигается не менее 95%.
Каждая точка в эвристико-статистическом анализе, если она не получена с грубой технической ошибкой при измерении, имеет содержательный смысл. Поэтому отклоняющиеся точки нельзя исключать без объяснений необходимости такого действия. Тогда оказывается, что обоснование критерия адекватности по 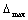 и 100 -
и 100 - 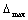 не только упрощает расчеты, но и дает полную гарантию адекватности модели по всем без исключения наблюдениям.
не только упрощает расчеты, но и дает полную гарантию адекватности модели по всем без исключения наблюдениям.
Пример 3. Моделирование переменных издержек. Из книги по микроэкономике [7, с.142-146] рассмотрим возможность моделирования биотехническим законом полных и средних переменных издержек производства для краткосрочных интервалов времени. Термины и условные обозначения приняты из указанной книги без изменений. Главная цель - показать переход от табличной формы статистических данных, известных в общей эконометрии, к математической модели.
Полные переменные издержки TVC (долларов ежедневно) в зависимости от объема выпуска Q (число единиц ежедневно) после моделирования описываются формулой (табл. 2)
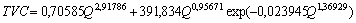 ,(9)
,(9)
для которой Q = 1,2,...,24 , а 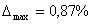 .
.
Средние переменные издержки AVC (в нашей стране принято говорить об удельной себестоимости) за единицу продукции (табл. 2) в долларах за день описывается формулой
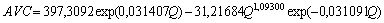 , (10)
, (10)
Таблица 2. Фактические и расчетные значения переменных издержек
|
Объем выпуска Q , шт./день |
Полные переменные издержки, доллар/день |
Средние переменные издержки, доллар/(шт. день) |
||||||
|
TV^C |
TVC |
|
|
AV^C |
AVC |
|
|
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
380 720 1025 1300 1550 1780 1995 2200 2400 2605 2820 3050 3300 3575 3880 4220 4600 5025 5500 6030 6620 7275 8000 8800 |
383 720 1024 1298 1548 1778 1994 2200 2404 2609 2823 3051 3299 3572 3876 4216 4597 5024 5501 6033 6625 7279 8001 8794 |
-3.3 -0.2 1.2 1.7 1.7 1.6 1.0 -0.4 -3.6 -4.2 -3.2 -1.2 1.0 2.8 3.9 4.0 3.0 1.2 -1.1 -3.3 -4.7 -4.4 -1.1 6.3 |
-0.87 -0.03 0.12 0.13 0.11 0.09 0.05 -0.02 -0.15 -0.16 -0.11 -0.04 0.03 0.08 0.10 0.09 0.07 0.02 -0.02 -0.05 -0.07 -0.06 -0.01 0.07 |
380 360 342 325 310 296 285 275 266 260 256 254 254 255 259 264 271 279 289 302 315 331 348 367 |
380 360 342 325 310 296 284 275 267 261 256 254 254 255 259 264 271 279 290 302 315 331 348 367 |
0.28 -0.49 -0.08 -0.05 0.32 -0.09 0.65 0.50 -0.57 -0.53 -0.40 -0.16 0.22 -0.25 0.45 0.35 0.47 -0.17 -0.55 0.36 -0.45 0.08 -0.07 0.14 |
0.07 -0.14 -0.02 -0.02 0.10 -0.03 0.23 0.18 -0.21 -0.20 -0.16 -0.06 0.09 -0.10 0.17 0.13 0.17 -0.06 -0.19 0.12 -0.14 0.02 -0.02 0.04 |
Полезность есть нечто такое, что мы чувствуем, а не то, что мы говорим [7, с.108]. Главной целью частной фирмы является максимизация прибыли. Главными препятствиями для достижения этой цели будут, во-первых, издержки производства, а во-вторых, спрос на произведенную продукцию [7, с.130].
Мы «чувствуем», что для российских предприятий, да тем более для лесных, модели (9) и (10) становятся законами изменения переменных издержек только в среднем (по детерминированной части). Они дополняются сильнейшими циклическими стохастическими изменениями как в издержках, так и в объеме выпускаемой продукции.
Законы статистического распределения неумолимы. Поэтому, если представить значения и как статистические выборки для фирм России, то формулу (9) можно будет использовать для выделения остатков и анализа динамики, специфичной для отечественных производств. Это является главным методологическим принципом, который заставляет отечественных исследователей изучать законы изменения экономических показателей зарубежных фирм, а затем как детерминированную составляющую использовать в математических моделях функционирования отечественных предприятий.
Из данных табл. 8 видно, что максимальная относительная погрешность модели по переменным издержкам равно 0,87%, а по средним - 0,23%. По табл. 2 надежность расчетов, если не учитывать первую точку по полным переменным издержкам, достигает класса А, то есть степень надежности расчетов (даже по значению ) составляет практически достоверные результаты при доверительной вероятности свыше 99,7%. Поэтому модели (9) и (10) высокоадекватны.
На рис. 1 приведены графики изменения составляющих этих математических моделей. Из них видно, что по графику 1 на рис. 1а полные переменные издержки растут по закону аллометрического роста. При этом на некотором интервале количества продукции происходит «стрессовое возбуждение» [8] производственной системы. Из-за участия людей она, конечно же, является эргатической, а по нашему ранее данному определению - биотехнической, прежде всего из-за действий «популяции персонала». В связи с этим стрессовое возбуждение на средних (удельных) переменных издержках проявляется (рис. 1б, график 2) вычитанием дополнительного воздействия.
В итоге персонал является регулятором издержек.
Полные издержки TC = TVC + TFC , где TFC - полные постоянные издержки [7, с.144]. Тогда модель (9) в общем виде можем записать как уравнение
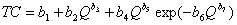 , где
, где 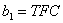 . (11)
. (11)
Сопоставление (11) и (1) показывает полную их структурную схожесть. В данном случае по формуле (11) значение b 1 характеризует заданные условия работы некоторого предприятия, систематические производственные потери и др.

Рис. 1. Графики изменения полных переменных издержек (а), средних переменных издержек (б) и их составляющих: 1, 2 - первая и вторая составляющие формул
Вторая слагаемая модели (11) учитывает увеличение сил инерции производства с ростом его масштаба. Третья слагаемая показывает биотехнический закон.
Отсюда следует, что между техническими, биологическими и экономическим процессами наблюдается аналогия по характеру влияния различных факторов.
Для анализа семейства кривых издержек достаточно идентифицировать модель (88). В нашем примере [7] полные издержки описываются моделью
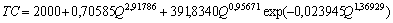 , (12)
, (12)
с доверительной вероятностью не менее 99,7%. Удельные (средние) издержки образуются после деления на значение Q , поэтому модель (10) может быть и не идентифицирована, то есть тогда получим два варианта моделей. Поэтому имеем
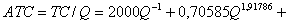
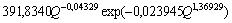 , (13)
, (13)
где - средние полные издержки, доллар/(шт. день). Тогда из модели (13) получим , что
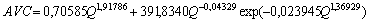 , (14)
, (14)
и эта модель будет аналогична модели (10). Однако преимущество конструкции (10) заключается в том, что можно вычислить показатель AVC при Q = 0 .
Для многих лесных предприятий России известны только значения TC , то есть полные издержки. При этом значение Q изменяется ежедневно стохастически. Модель (11) следует дополнить составляющей циклического типа (корреляционные функции колебаний производственного процесса). Тогда возможно моделирование полных издержек на лесное дело, как элемента природопользования, по матрице фактических данных, получаемой в реальном режиме времени.
Статья опубликована при поддержке гранта 3.2.3/4603 МОН РФ
СПИСОК ЛИТЕРАТУРЫ:
- Мазуркин, П.М. Статистическое моделирование. Эвристико-математический подход / П.М. Мазуркин. - Научное издание. - Йошкар-Ола: МарГТУ, 2001. - 100с.
- Печенкин, В.Е. Бесстружечное резание древесины / В.Е. Печенкин, П.М. Мазуркин. - М.: Лесн.пром-сть, 1986. - 144 с.
- Столяров, Д.П. Использование кернов древесины в лесоводственных исследованиях: Методические рекомендации / Д.П. Столяров, О.Н. Полубояринов и др.. - Л.: ЛенНИИЛХ, 1988. - 43 с.
- Моисеев, Н.Н. Математические задачи системного анализа / Н.Н. Моисеев. - М.: Наука, 1981. - 488 с.
- Элти Дж., Кумбе М. Экспертные системы: концепции и примеры. - М.: Финансы и статистика, 1987. - 191 с.
- Жирмунский, А.В. Критические уровни в развитии природных систем / А.В. Жирмунский, В.Н. Кузьмин. - Л.: Наука, 1990. - 223 с.
- Долан Э.Дж., Линдсей Д. Микроэкономика / Пер. с англ. В.Лукашевича и др.; Под общ. ред. Б.Лисовика и В.Лукашевича. - СПб.: АОЗТ «Литера плюс», 1994. - 448 с.
- Практикум по лесоводству. - М.: Высшая школа, 1989. - 311 с.




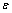 ,лет
,лет
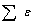 ,лет
,лет
 , %
, %
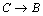
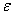
 , %
, %